Flexural behavior of wood in the transverse direction investigated using novel computer vision and machine learning approach

2.1 Specimen preparation

This study investigated mature Hinoki (Chamaecyparis obtusa) wood. Three sample types (flat-sawn, rift-sawn, and quarter-sawn) were first prepared only from sapwood with consideration to the orientation of the annual ring, which was confirmed by visual observation. The angle of the annual ring aligned in the horizontal direction and vertical direction was 0° and 90°, respectively. The sample with an annual ring angle of 0°–30° was defined as flat-sawn, that with a ring angle of 30°–60° was defined as rift-sawn, and that with a ring angle of 60°–90° was defined as quarter-sawn. Five flat-sawn, quarter-sawn, and rift-sawn, specimens were prepared with the dimensions of 10 mm (longitudinal) × 20 mm (width) × 1.5 mm (thickness), respectively. The cross-section of all specimens was smoothed by a sliding microtome (TU-213, Yamato Kohki industrial Co., Ltd., Japan). Then, all specimens were conditioned in a plastic glove box at 60% relative humidity (RH) and 25 °C using sodium bromide solution for more than two weeks. The average density and moisture content of specimens with standard deviation (SD) in parenthesis were 399 (17) (kg/m³) and 11.1 (0.3) %, respectively.

2.2 Micro three-point bending test

After the conditioning, all specimens were subjected to the micro three-point bending test. A customized metal jig (Figure1a) was used for testing. A motor (BLM230P-GFV2, ORIENTAL MOTOR Co., Ltd., Japan) with a test speed of 1 mm/min was used to horizontally bend the specimens. A 200-N load cell (LUR-A-200NSA1, Kyowa Electronic Instruments Co., Ltd., Japan) with a sensor interface (PCD-320 A, Kyowa Electronic Instruments Co., Ltd., Japan) was used to record the force; the sampling speed was 1 Hz. During the test, a stereo-microscope (Leica DMS300, Leica Camera AG, Germany) was set perpendicularly to the cross-section to record the deformation of the tracheid cells on video at 30 fps. The resolution was 1080p; the length of one pixel is equal to approximately 2.09 µm. All experiments were conducted at 60% RH and 25 °C.

Figure 1:

Illustration of micro three-point bending test: (a) Illustration of mechanical test apparatus: (b) cross-section of wood specimen observed with stereo-microscope.

2.3 Deep learning based semantic segmentation model

To prepare the model training dataset, after capturing the video during the bending test, the first image at every second of the video was captured to compile an image sequence. Twelve original images with 256 × 256 pixels were randomly cropped from the image sequence. The watershed segmentation implemented by the Python Mahotas package was first applied to label the boundary of the tracheid cells (Figure 2b) (Coelho 2013; Vincent and Soille 1991). The unlabeled part was manually modified to make the corresponding ground truth masks. The boundaries were labeled at the centerline of the adjacent cell walls. For a tracheid cell wall adjacent to the ray parenchyma cells, owing to the low contrast of the ray parenchyma cell lumen, the boundaries were always labeled at the center part of the ray parenchyma cell, which means that part of a ray parenchyma cell was recognized as a tracheid cell (Figure 2b). In future work, the parenchyma cell walls should be labeled separately and the microscopic observation method should be improved.

Figure 2:

Preparation of dataset for semantic segmentation model training: (a) cropped patch of wood cross-section; (b) trachied cell boundary mask labeled by watershed segmentation algorithm; (c) manually corrected image mask. The scale bar indicates a length of 100 μm.

Twelve sets of original images, and the corresponding ground truth masks with the cell boundaries labeled in white and the background labeled in black, were used to build the semantic segmentation model. For model training, the symmetric U-Net architecture, which is achieved by using the “same” padding instead of “valid” in the original model (Ronneberger et al. 2015) was used. The network was implemented using the Tensorflow framework (ver. 1.5.0) and Keras (ver. 2.2.4). The binary cross-entropy was used as the loss function, and Adam was used as the optimizer. The learning rate was 0.0001. During model training, the images were augmented by the image generator. The details of augmentation parameters were shown in Supplementary Table S1.

2.4 Model evaluation metrics

Four metrics, namely, precision, recall, F1, and accuracy, were used to evaluate the trained model. These metrics were calculated from the true positive (TP), false positive (FP), true negative (TN), and false negative (FN) obtained from the confusion matrix for the binary classification of the cell boundary and background. The following equations were used:

2.5 Image prediction and individual cell tracking

After model training, the trained model assisted by a patch blending algorithm (Chevalier 2017) was used to partition all potential cells in the image sequence with 1920 pixels × 1080 pixels. After predicting all image sequences, watershed segmentation was used to achieve the instance segmentation of all cells. Finally, the coordinates of the centroid of the segmented cells were collected, and a tracking algorithm (Crocker and Grier 1996) implemented using the Python Trackpy package was used to link the same cell walls in each image (Allan et al. 2021). Figure 3 is the sample data indicating the processes of watershed segmentation (Figure3a), coordinate extraction of centroids (Figure3b), and individual cell tracking (Figure3c) described above with 256 X 256 pixels image.

Figure 3:

Tracking of cell deformation during mechanical test: (a) watershed segmentation of predicted image by trained U-Net model to achieve instance segmentation; (b) centroid coordinates for each cell extracted as features for individual cell tracking; (c) centroid trajectories obtained by Crocker–Grier linking algorithm; the color of each trajectory was randomly generated.

2.6 Parameter measurement for cell deformation analysis

After tracking the individual cells that existed in every image sequence, the area, eccentricity, major and minor axis length of the fitted ellipse (Figure 4 ① ②), and the vertical and horizontal length of the bounding box (Figure 4 ③ ④) for each cell wall were measured. The eccentricity was calculated from the fitted ellipse with the same second moments as the cell wall. The eccentricity of a circle is zero, while the eccentricity of an ellipse is greater than zero but less than one. These measurements were made using the Python scikit-image package (Van Der Walt et al. 2014). The fitted ellipse aspect ratio and bounding box aspect ratio were calculated based on the following equations:

Figure 4:

Measurement parameters for evaluating intensity of cell deformation.

To evaluate the intensity of the cell deformation, the changes in the area, eccentricity, fitted ellipse aspect ratio, and bounding box aspect ratio were calculated based on the following equation:

where n indicates the order of the observed image sequence and i indicates the type of the measured parameters shown in Figure 4.

3.1 Flexural behavior of flat-sawn, quarter-sawn, and rift-sawn specimens in the transverse direction

Figure 5 shows the difference in the mechanical properties of the flat-sawn, quarter-sawn, and rift-sawn specimens in the transverse direction. During the micro three-point bending test, the rift-sawn specimens exhibited the smallest load values with the largest displacement of approximately 3.3 mm, which resulted in the smallest modulus of elasticity (MOE) and modulus of rupture (MOR) (Figure 5a). Assuming that the linear stage of calculated stress-strain is the elastic region and the nonlinear stage is the plastic region, the rift-sawn specimens had the largest plastic region. In contrast, the quarter-sawn specimens exhibited the largest MOE and MOR (Figure 5b) and had the smallest plastic region. These results are consistent with the results obtained by a previous study (Hwang et al. 2021), which suggests that the orientation of the annual ring contributes significantly to the flexural behavior of wood in the transverse direction, and also demonstrates that the micro three-point bending test system is reliable for the investigation of the mechanical properties of wood in the transverse direction.

Figure 5:

Mechanical properties of flat-sawn, quarter-sawn, and rift-sawn hinoki specimens in the transverse direction: (a) load–displacement curve of three types of hinoki specimens during micro three-point test; (b) MOE and MOR of three specimen types. The error bars indicate the standard deviation.

3.2 Validation of U-Net model and large image prediction

With the development of artificial intelligence, fully convolutional network (FCN) models have been proposed for semantic segmentation (Long et al. 2015). The U-Net architecture was proposed by Ronneberger et al. 2015 as an improvement of FCN and is designed to use fewer training samples for model training. The U-Net architecture is a U-shaped architecture consisting of encoder blocks, decoder blocks, and skip connections, and has become a popular approach for semantic segmentation tasks. Recently it was extensively investigated to conduct even 3D segmentation of several kinds of plant tissues and achieved excellent accuracy (Wonly et al. 2020).

Figure 6a shows the evolution of the binary cross-entropy loss during training for 100 epochs with the U-Net architecture. After training for approximately 40 epochs, the validation loss tended to become approximately constant and training loss continued to decrease to approximately 0.1. The average values (SD) of precision, recall, F1, and accuracy of five test images are 0.82 (0.02), 0.82 (0.02), 0.82 (0.02), and 0.92 (0.01), respectively, which indicates that the constructed semantic segmentation model is accurate. Figure 6b shows an example of the original input image, and Figure 6c shows the image predicted by the trained model. The large image of the cross-section was satisfactorily predicted by combining the patch blending algorithm and the trained model Supplementary Figure S1. Most tracheid cells appeared to be satisfactorily segmented, whereas the partition of the latewood tracheid cells and some earlywood cell walls were not satisfactorily predicted, owing to the low contrast of the cell wall lumen. To overcome this problem, the microscopic observation method must be improved to increase the contrast of the cell wall lumen.

Figure 6:

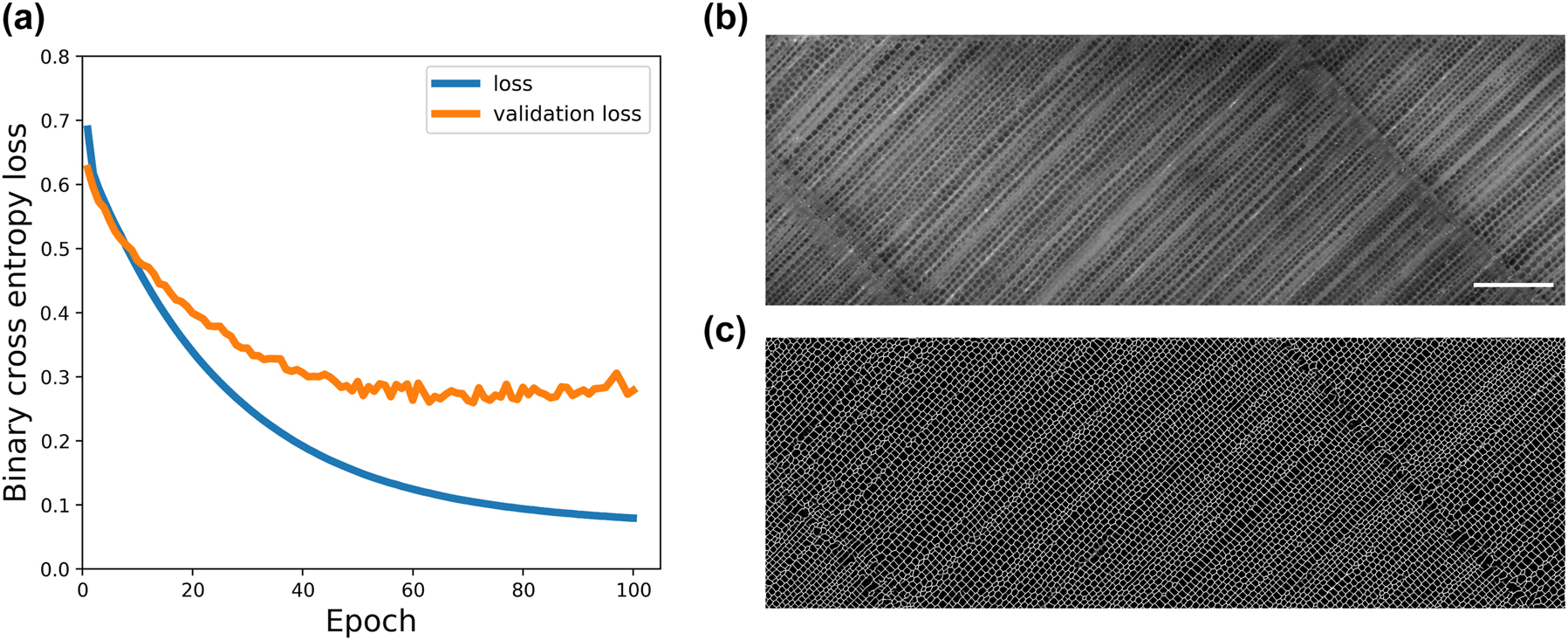
Tracheid cell boundary prediction by trained U-Net model: (a) binary cross-entropy loss plotted against training epochs; (b) original image input; (c) predicted image. The scale bar indicates the length of 400 μm.

The geometrical parameters of a flat-sawn specimen were measured to further confirm the segmentation accuracy. The vertical bounding box and horizontal bounding box were considered as the cell radial diameter and cell tangential diameter. Figure 7 shows the distribution of the typical parameters measured from the segmented cells. The averaged values (SD) of the area, cell eccentricity, cell radial diameter, and cell tangential diameter are 955 μm (306), 0.60 (0.15), 37.5 μm (7.6), and 34.8 μm (6.6), respectively. These parameters are consistent with the geometrical parameters reported by a previous study (Saiki 1963).

Figure 7:

Histogram and density plot indicating the distribution of typical parameters measured from flat-sawn specimen before mechanical test: (a) cell area (µm²); (b) cell eccentricity; (c) cell diameter (µm) (yellow: cell radial diameter; gray: cell tangential diameter).

3.3 Typical deformation patterns of tracheid cell in three specimen types

Figure 8 shows the typical deformation patterns of a tracheid earlywood cell wall located in both compression and tension part of the three specimen types during the micro three-point bending test. For the flat-sawn specimens, the compressive and tensile stress likely induced the uniaxial compression and elongation of the cell in the tangential direction, respectively. Due to the Poisson effect, the radial cell width of the cell located at the tension part decreased (Figure 8a). Owing to the orthogonal orientation of the cell, similar deformation seems to be observed in the radial direction of quarter-sawn specimens. Because the quarter-sawn specimens fractured at the early stage of the bending test, when the displacement was only approximately 1 mm, the dimensional changes of the cell were much smaller than those of the flat-sawn specimens while the Poisson effect was confirmed at both compression and tension part (Figure 8b).

Figure 8:

Typical deformation pattern of tracheid cell for (a) flat-sawn, (b) quarter-sawn, and (c) rift-sawn specimens before fracture. The scale bar indicates a length of 50 μm.

Unlike the flat-sawn and quarter-sawn specimens, the cell wall in the rift-sawn specimens exhibited different deformation patterns. The shear deformation of the cell walls was both observed in compression part and tension part (Figure 8c). Murata and Masuda (2003) analyzed the strain distribution of softwood in transverse compression by DIC method. And the large shear strain was observed in the case of the compression of rift-sawn type specimen, and they proposed the rolling shear of the cell wall contributed to such large shear strain distribution, which is consistent with our observation. Furthermore, this orientation of the tracheid cells is somewhat similar to the uniaxial loading of honeycombs in the in-plane off-axial direction. Li et al. (2018) simulated the in-plane yield strength of square honeycombs in different directions under compression using a theoretical approach and the FEM method. They concluded that square honeycombs exhibit strong anisotropy when loaded in different orientations. Their numerical simulation results revealed that the axial yield strength of the square honeycomb has minimum values at an angle of orientation of 37°–38°, which is in the range of the orientation of the annual ring of the rift-sawn specimens. Therefore, it is thought that the shear deformation induced by the off-axis loading of the tracheid cell is responsible for the large displacement and low MOE and MOR of rift-sawn specimens.

3.4 Visualization of distribution of tracheid cell deformation

Using the Crocker–Grier linking algorithm, the coordinates of the centroids for each common tracheid cell that existed in each frame of the image sequence were linked, and thousands of common cells were extracted. These common cells were mainly the earlywood cells, which had sufficient cell wall lumen contrast. The latewood cells and earlywood cells, which had low cell wall lumen contrast along the radial direction, were not linked owing to their bad segmentation.

After evaluating the intensity of the deformation by calculating the changes in the four parameters (area, eccentricity, fitted ellipse aspect ratio, and bounding box aspect ratio) described in Section 2, suitable parameters for evaluating cell deformation were selected by considering the different types of cell deformation in three specimen types. The area and bounding box aspect ratio were selected for evaluating the cell deformation of flat-sawn and quarter-sawn specimens, respectively. As the rift-sawn specimens exhibited the relatively large shear deformation of cell, area, eccentricity, and fitted ellipse aspect ratio are promising parameters for the evaluation of deformation. Among them, the fitted ellipse aspect ratio was selected for further analysis in this study. A detailed discussion of parameter selection was summarized in Supplementary Figures S2, S3, S4, and S5.

After parameter selection, the 2D mapping of the cell deformation intensity for the three specimen types at the elastic region, plastic region and before fracture was constructed (Figure 9). The white color indicates that the measured parameters were unchanged; the darker red and darker blue color indicate larger increase and larger decrease in the measured parameters, respectively. In the elastic region, all specimens exhibited relative slight and varied deformation for all parameters (Figure 9a, d, g), which suggests the force was uniformly transferred to each cell wall. In the plastic region, the cell deformation distribution was different (Figure 9b, e, h). And the intensity of the deformation reached the maximum before fracture of specimen (Figure 9c, f, i).

Figure 9:

Intensity of cell deformation of flat-sawn, quarter-sawn and rift-sawn specimens during micro three-point bending test evaluated by three selected parameters and their distribution: (a, b, c) changes in area (%); (d, e, f) changes in bounding box aspect ratio (%); (g, h, i) changes in fitted ellipse aspect ratio (%); (a, d, g) elastic region; (b, e, h) plastic region; (c, f, i) before fracture.

For the flat-sawn specimens, the area appears to be the most suitable parameter for deformation evaluation. As shown in Figure 9b, c, the cell area increased in the tension part and decreased in the compression part of the specimen. Those results might be owing to the existence of latewood at the compression part, which contributed to the restriction of cell deformation. On the whole, it was found that 60% of the cells showed increases in cell area while 39% of the cells showed decreases in cell area in the observed cross-section.

For the quarter-sawn specimen, the bounding box appears to be a promising parameter. Because the specimen exhibited minor curvature during the bending test, the compressive stress caused the ratio to increase, whereas the tensile stress caused the ratio to decrease. The neutral axis seems to be approximately located at the central part of the specimen with the smallest intensity of the changes. Overall, 50% of the observed cells showed increases in the ratio and 50% of the cells showed decreases in the ratio.

For the rift-sawn specimen, the fitted ellipse aspect ratio was selected for the evaluation of deformation. An increase in the fitted ellipse aspect ratio was observed both in the compression part and tension part (Figure 9h, j) Rather than in the flat-sawn and quarter-sawn specimens, the more concentrated and intensive deformation was observed at the innermost area of the compression part and outermost area of the tension part of the rift-sawn specimens. In the observed area, 70% of the cells showed increases in fitted ellipse ratio and 30% of the cells showed decreases in the ratio. The reason for this is that the shear formation of the cell was the dominant deformation pattern and responsible for the increase major axis length, and the decrease in the minor axis length.

3.5 Clustering analysis of deformation pattern of individual cells

To summarize the deformation pattern of each individual cell, the k-means clustering algorithm was implemented through the Python scikit-learn package (Pedregosa et al. 2011). According to Figure 10a, e, i, the clustering algorithm effectively summarized eight clusters corresponding to the intensity of cell deformation for the three specimen types. Figure 10b, f, j showed the fracture pattern of specimens after three-point bending test. The fractures of the three specimen types had high occurrence probability in the corresponding tension part of their clustered color that exhibited large cell deformation. The cluster distribution for the three specimen types is shown in Figure 10c, d, g, h, k, l showed the relationship between the eight summarized deformation patterns and the strain of specimen during the three-point bending test. In the elastic region with the light green color, linear changes in the cell area, bounding box, and fitted ellipse aspect ratio for the flat-sawn, quarter-sawn, and rift-sawn specimens were observed as the strain increased. However, the cell deformation pattern of those specimens was different in the plastic region with skyblue color.

Figure 10:

Results of k-means clustering for deformation patterns and their relationship with fracture pattern and strain of specimens: (a, e, i) clusterized images of flat-sawn, quarter-sawn, and rift-sawn specimens, respectively. The yellow circle in (i) points out the blue-colored cells of rift-sawn located at the outermost area of tension part showing minor deformation; (b, f, j) fracture pattern of flat-sawn, quarter-sawn and rift-sawn specimens, respectively. The scale bar indicates a length of 400 μm; (c, g, k) distribution of clusters of changes in area, bounding box aspect ratio, and fitted ellipse aspect ratio for flat-sawn, quarter-sawn, and rift-sawn specimens, respectively; (d, h, l) clusterized changes in area, bounding box aspect ratio, and fitted ellipse aspect ratio during mechanical test for flat-sawn, quarter-sawn, and rift-sawn specimens, respectively, and their relationship with strain. The light green and skyblue areas indicate the assumed elastic and plastic regions, respectively.

For the flat-sawn specimens, almost linear changes in cell area with the evolution of strain were observed in plastic region (Figure 10d). The clustered cells with red color were located at the outermost area of tension part to finally have around a 9% increase in cell area. And the area of cell with vermillion color located at innermost area of compression part showed about 5% decrease. As shown in Figure 10b, the ray parenchyma cells appear to be a defect that facilitates fractures, and the detachment between cells along the radial direction was also observed.

The linear changes in the bounding box aspect ratio were also observed in the plastic region of quarter-sawn specimen (Figure 10h). The significant increase and decrease in the bounding box aspect ratio mainly occurred in the earlywood region near the previous latewood region, which was colored with red and vermilions, respectively (Figure 10e). With the evolution of strain, the bounding box aspect ratio of the cells with those two colors showed 12% increase and 8% decrease, respectively. The earlywood cell wall located in that region exhibited a thinner cell wall with a large cell area, which resulted in weaker mechanical properties. This is assumed to be the reason for the initiation of the fracture of the specimen, which possibly induced the detachment between cells in the earlywood region of the tension part (Figure 10f). Because the ray parenchyma cells of the quarter-sawn specimens were aligned against the mechanical load, the ray parenchyma cells may have contributed significantly to the restriction of the cell deformation, which resulted in larger MOE and MOR compared with that of the flat-sawn specimens.

For the rift-sawn specimens, with the increases in strain, pink colors showed a logarithmic increase while two clusters with red and vermilion colors along the radial files typically exhibited exponential increase (Figure 10l). When the strain reached around 5%, changes in fitted ellipse aspect ratio for the pink-colored cells tend to become almost constant and finally reached 21%. And the red- and vermilion-colored cells showed a drastic increase in the changes in fitted ellipse aspect ratio and finally reached 28 and 43% before the fracture, respectively. Such large shear deformation contributed significantly to the flexibility of the rift-sawn specimens. Owing to the orientation of the annual ring at approximately 44.5°, the ray tissue appeared to impose a minor restriction on the cell walls. Interestingly, as in Figure 10i, the blue cells in the yellow circle were located at the outermost area of the tension part. Although those cells remained relatively unchanged, they were surrounded by red and vermillion-colored cells that had been largely deformed. Such a restricted blue area is possibly involved in the initiation of the cell detachment in Figure 10j. Closer observation of the fractured surface allows us to conclude that the detachment between cells along the radial direction dominated the fracture pattern of the specimens.