On 2-regular graphs whose girth is one less than the maximum
-
A.V. Knyazev
Abstract
We say that a digraph is 2-regular (dichotomous) if the out-degrees d0(j) and in-degrees d1(j) of any its vertex j ∈ V satisfy the equality d0(j) = d1(j) = 2. A graph Г is said to be primitive if for any pair i and j of its vertices in Г there exists a path from i to j of length m > 0. The least m is denoted y(Г) and called the exponent of Г. Let G(n, 2, p) stand for the class of strongly connected 2-regular graphs with n vertices of girth (the length of the shortest circuit) p, and let P(n, 2, p) denote the class of primitive 2-regular graphs of girth p with n vertices. The girth of a 2-regular graph with n vertices does not exceed ]n/2[, where ]x[ is the least integer no smaller than x. Earlier, the author proved that any primitive 2-regular graph with n vertices and with the maximal possible girth ]n/2[ had the exponent equal exactly to n - 1.
In this paper we prove that for odd n ≥ 13
G(n, 2, (n- 1)/2) = P(n, 2, (n- 1)/2),
any graph in G(n, 2, (n -1)/2) has a circuit of length (n + 1)/2, and for any Г ∈ G(n, 2, (n- 1)/2) the inequality
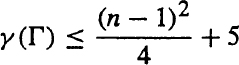
is true.
© 2016 by Walter de Gruyter Berlin/Boston
Articles in the same Issue
- Editorial
- On inherited properties of restricted Boolean functions
- Some properties of the inertia groups of Boolean bijunctive functions and an inductive method of generating such functions
- On complexity of representation of multiple-valued logic functions as polarised polynomials
- On the periodicity of the sequence of states of an automaton corresponding to a given initial state and a given periodic input sequence
- On the analysis of fuzzy information graphs
- Lattices of Ω-foliated formations
- A formal reduction of the general problem of expressibility of formulas in the Gödel-Löb provability logic
- On some conditions for absence of a giant component in the generalised allocation scheme
- On 2-regular graphs whose girth is one less than the maximum
- Forthcoming Papers
- Contents
Articles in the same Issue
- Editorial
- On inherited properties of restricted Boolean functions
- Some properties of the inertia groups of Boolean bijunctive functions and an inductive method of generating such functions
- On complexity of representation of multiple-valued logic functions as polarised polynomials
- On the periodicity of the sequence of states of an automaton corresponding to a given initial state and a given periodic input sequence
- On the analysis of fuzzy information graphs
- Lattices of Ω-foliated formations
- A formal reduction of the general problem of expressibility of formulas in the Gödel-Löb provability logic
- On some conditions for absence of a giant component in the generalised allocation scheme
- On 2-regular graphs whose girth is one less than the maximum
- Forthcoming Papers
- Contents


