Abstract
Hyperbolic numerical idioms in modern Chinese are a phenomenon of hyperbolic rhetoric, where numeral words indicate extremely large or small quantities. This study uses Bayesian models to examine the semantic reasoning and pragmatic reasoning processes of hyperbolic numerical idioms. In terms of semantic reasoning, a conditional probability formula is used to demonstrate that hyperbolic quantities can infer any other quantity, leading to the conclusion that the idiomatic events with any quantity are generally valid; in terms of pragmatic reasoning, Bayes’ theorem is employed to show that hyperbolic numerical idioms significantly influence the listener’s numerical cognition, leading to a tendency for the listener’s estimation of the quantity related to the idioms to shift towards hyperbolic quantities. Finally, this study explores the applicable contexts for hyperbolic numerical idioms and analyzes the Bayesian mechanisms behind illegal hyperbolic expressions, pointing out that hyperbolic expressions must carry implications of impossibility and counterfactuality; if the hyperbolic expression conveys a commonplace event, it results in communication failure.
1 Introduction
Unlike mathematics, numerals in natural language can indicate not only exact meanings but also plain approximative implicature (Krifka 2007; Ran 2010; Lauer 2012; Carter 2019), and hyperbolic approximative implicature (Lavric 2010; Jiang and Xu 2024), according to the classification types established by Channell (1983: 87–94). The phenomenon of numerals indicating approximative implicature is idiomatic (Hsiao and Su 2010), and is influenced by cross-linguistic and cross-cultural factors, therefore, it is necessary to examine relevant phenomena in more languages (Lavric 2010; Wang et al. 2024).
The subject of this study is Chinese hyperbolic numerical idioms, in which numerals indicate hyperbolic approximative implicature. Impossibility and counterfactuality are important characteristics of hyperbolic rhetoric (McCarthy and Carter 2004), in this regard, Lavric (2010) notes that the conversational implicature characteristics of hyperbolic numerals are: (1) the speaker cannot possibly know the number; (2) the number cannot be true. More specifically, the magnitude of the quantity in hyperbolic expressions is exaggerated, typically for emphatic or emotive function (Kann 2022). Numerals in hyperbolic numerical idioms generally indicate maximum and minimum implicature (Zhang 2020), which can respectively be referred to as “auxesis” and “meiosis,” derived from McCarthy and Carter (2004). Typically, low numbers like 一(yī, one) indicate meiosis implicature, while high numbers like 百 (bǎi, hundred), 千 (qiān, thousand) and 万 (wàn, ten thousand) indicate auxesis implicature. However, middle numbers (derived from Lavric (2010), typically a number within the range of 7–40) can indicate both meiosis implicature (e.g., 三户亡秦 (sān hù wáng qín), 七步之才 (qī bù zhī cái), 十步芳草 (shí bù fāng cǎo)) and auxesis implicature (e.g., 火冒三丈 (huǒ mào sān zhàng), 七纵七擒 (qī zòng qī qín), 十全十美 (shí quán shí měi)), which depend on the context, culture, and other factors. When numerals indicate hyperbolic approximative implicature, they exhibit a high degree of polarity sensitivity (Jiang and Xu 2024). According to the implicature and polarity combination criteria proposed by Israel (2011: 85), these four idiom examples 一 文 不 值 (yī wén bù zhí), 一 针见血 (yī zhēn jiàn xiě), 万 死 不 辞 (wàn sǐ bù cí), and 遗臭 万 年 (yí chòu wàn nián) can be respectively classified as follows: negative meiosis, affirmative meiosis, negative auxesis, and affirmative auxesis, and a more detailed representation of hyperbolic numerical idioms is shown in Figure 1, in which the vertical axis represents the magnitude of quantity. Semantic reasoning is a straightforward interpretation of natural language expressions, however, when multiple factors such as context and sociocultural elements are involved, pragmatic reasoning plays a significant role in the process of expression, although it relies on semantic information (Bergen et al. 2016). In terms of hyperbolic numerical idioms, the reasoning process can be divided into semantic reasoning and pragmatic reasoning:
The semantic reasoning of hyperbolic numerical idioms refers to scalar reasoning. Scalar reasoning is a method that infers the situation of one level of entities based on the hierarchical relationship between entities (Jiang and Gong 2006). In terms of hyperbolic numerical idioms, it means that the hyperbolic values can infer other quantity values, ultimately leading to the establishment of idiomatic events for any quantity value, i.e., totality. For example, the metaphorical meaning of 一毛不拔 (yī máo bù bá, which means not willing to give even a dime) can infer “not willing to give any amount of money.” According to the aforementioned four combination types, hyperbolic numerical idioms exhibit the following scalar reasoning patterns:
Affirmative auxesis → Affirmative total
Negative meiosis → Negative total
Affirmative meiosis → Affirmative total
Negative auxesis → Negative total
The pragmatic reasoning of hyperbolic numerical idioms refers to the change in the listener’s cognitive estimation of the quantity that the idiomatic event can denote. Still taking 一毛不拔 (yī máo bù bá) as an example, if it is assumed that “a certain person usually donates 100 yuan in charity,” the speaker’s expression “this person is not willing to give even a dime” may lead the listener to lower their estimation of the usual amount this person donates. Since hyperbolic expressions represent counterfactual events, according to the ostensive-inferential model of relevance theory, there is a noticeable difference between new information (hyperbolic numerical idioms) and old information (the listener’s existing cognitive context), then the listener tends to deny or abandon the old information to some extent (Sperber and Wilson 1986: 114). Consequently, meiosis numerical idioms will lower the listener’s quantity estimation, while auxesis numerical idioms will raise it.

Distribution of four types of hyperbolic numerical idioms.
Although the aforementioned reasoning theories are very detailed, they still lack the use of scientific and precise methods, such as mathematics, to analyze the semantic and pragmatic reasoning processes of idioms. This may, to some extent, weaken the argumentative strength of the reasoning theories. With the rise of interdisciplinary research paradigms, mathematical methods have gradually gained attention in linguistic studies. The semantic and pragmatic reasoning can have multiple representations in mathematics, for example: (1) The inclusion relationship of sets indicates that there exists a reasoning relationship between two sets. If the smaller set holds, then the larger set also holds; (2) The conditional probability formula illustrates the reasoning relationship between two events (which can also be considered a kind of set). If the probability equals 1, there exists a causal relationship between the two events, while if it lies between 0 and 1, there exists a correlation between them. However, while a causal relationship can indeed be viewed as a form of reasoning relationship, a correlation cannot be regarded as a reasoning relationship. It is particularly important to note that there are two interpretations of probability: (1) the frequentist perspective asserts that probability is the frequency value observed in sufficiently large samples, which is objective and should be sufficiently precise; (2) the Bayesian asserts that probability is subjective, depending on individual experience and encyclopedic knowledge, and it changes as the individual’s experiences and encounters evolve (Mao and Tang 2012). Therefore, the Bayesian model is more suitable for studying semantic and pragmatic reasoning processes, as it can take into account subjective and other uncertain pragmatic factors (Huang and Jiang 2011). Its ideas are very similar to those of relevance theory, and it can quantitatively validate and refine relevance theory (Xu and Yan 2023), thus it allows for a better study of the reasoning processes involved in rhetorical devices such as hyperbole, litotes, irony, and others.
Combining the above analysis, this study employs a Bayesian model to investigate the semantic and pragmatic reasoning processes of Chinese hyperbolic numerical idioms, aiming to reveal the reasoning mechanisms underlying hyperbolic expressions from a mathematical perspective. The study is guided by the following three questions:
Semantic Reasoning: Previous studies have indicated that the extremely low probability of an event is a necessary condition for initiating scalar reasoning (Jiang 2010). However, how an event with an extremely low probability can infer events with higher probabilities has not been rigorously derived in prior research. Therefore, this paper seeks to clarify the probabilistic implications of scalar reasoning, revealing the strict reasoning process from hyperbolic values to totals.
Pragmatic Reasoning: Previous research has pointed out that hyperbolic expressions can convey a significant amount of information and a strong modality to the listener (Jiang and Xu 2024), but it has not specified how hyperbolic expressions affect the listener’s quantity cognitive estimation. Thus, based on the ostensive-inferential model, this paper employs the Bayesian model to calculate the inferential results of hyperbolic numerical idioms on the listener’s quantity cognition, exploring their position between old and new information, thereby reflecting the intensity of pragmatic reasoning.
Strategy Research: There may be erroneous hyperbolic expressions in communication, which essentially violate the normal reasoning path of semantic and pragmatic reasoning processes regarding hyperbolic expressions. Previous studies have examined the semantic reasoning characteristics of erroneous hyperbolic expressions (Jiang and Xu 2024), but the pragmatic reasoning characteristics have not yet been investigated. Pragmatic strategies are the means by which speakers generate implicatures through the interaction of implicit and explicit significances (Verschueren 1999: 156). Contextual factors play a decisive role in the selection of pragmatic strategies and speakers must choose appropriate strategies to ensure that the pragmatic inferences of listeners align with the speaker’s intentions (Lyons 1977: 290; Mey 1993: 81). From a Bayesian perspective, the difference between posterior and prior expectations serves as an indicator of the efficacy of pragmatic strategies (Degen 2023). Building on this insight, this paper aims to analyze the results of Bayesian pragmatic reasoning applied to such expressions. By identifying the abnormal probability distribution characteristics associated with these errors, we seek to reveal the fundamental reasons underlying their negative pragmatic effects.
2 A Review of the Semantic and Pragmatic Reasoning of Hyperbolic Expressions
The semantic reasoning of hyperbolic expressions refers to scalar reasoning. When numerals indicate exact meanings, they may involve scalar reasoning processes (Horn 1996; Carston 1998; Yeom 2006; Wu and Dai 2009). Conversely, when numerals indicate hyperbolic approximative implicature, they can also involve scalar reasoning processes, but this differs from the former case because: (1) As Lavric (2010) states, the numerals in the latter case are not true numbers, and the scalar meaning here represents a more abstract quantitative reasoning approach, akin to gradable adjectives (Kennedy 2007); (2) The scalar reasoning in the latter involves a wide range of quantitative reasoning, thus possessing a strong modality (Jiang and Xu 2024), whereas the former typically does not exhibit this characteristic. The model proposed by Israel (2001, 2011) among the scalar reasoning theories of the hyperbolic expressions is particularly well-developed, which includes two types of scalar logical rules: (1) When there is a negative correlation between the value represented by the hyperbolic word and the probability of the event described by the expressions: affirmative auxesis indicates affirmative total, and negative meiosis indicates negative total; (2) When there is a positive correlation: affirmative meiosis indicates affirmative total, and negative auxesis indicates negative total. Israel (2001: 320) summarizes the core principles that trigger scalar reasoning with hyperbolic expressions as follows: (1) Affirmative hyperbolic expressions represent an event that is highly unlikely to occur yet does; (2) Negative hyperbolic expressions represent an event that is highly likely to occur yet does not. Jiang (2010), Jiang and Xu (2024) deeply elaborate on Israel’s perspective from a probabilistic standpoint, portraying the relationship between value and event probability as a probability function. In these studies, the values in hyperbolic expressions are considered as an unknown variable x, and the probability of the event represented by the hyperbolic expression is p(x), then: (1) When the hyperbolic expression is a meiosis expression, p(x) is a monotonically increasing function; (2) When the hyperbolic expression is an auxesis expression, p(x) is a monotonically decreasing function. Regardless of the monotonicity of p(x) and the polarity of the hyperbolic expression, the probability of the event is always extremely low, which aligns with the perspective introduced earlier by McCarthy and Carter (2004). However, the characteristics of probability and monotonicity are merely necessary conditions to initiate scalar reasoning. The above studies have yet to conduct a probabilistic analysis of Israel’s scalar reasoning model, specifically addressing how events with extremely low probabilities can infer events with higher probabilities.
The pragmatic reasoning of hyperbolic expressions can be analyzed using the ostensive-inferential model, which is an important part of relevance theory. The ostensive-inferential model states that after the speaker ostensively conveys their intention to the listener, the listener seeks the best relevance and makes corresponding inferences based on the speaker’s ostensive expression (Sperber and Wilson 1986: 49). The specific process involves: (1) the speaker choosing an appropriate expression to clearly convey an intention (new information) to the listener; (2) the listener decoding the speaker’s new information, associating it with their existing cognitive context (old information), and reasoning in a particular direction concerning the new information to generate their understanding. The “downward-upward” pragmatic reasoning theory reasonably explains how the listener infers pragmatic meanings based on the best relevance in hyperbolic expressions (Jiang 2004). This theory proposes that old information (denoted as A) and new information (denoted as B) form a pragmatic hierarchical relationship: (1) First, the listener adopts a compliance strategy, temporarily moving A’s hierarchical position to B’s position, i.e., A = B, thereby grasping the speaker’s ostensive intention; (2) Secondly, since A = B and A < B (or A > B) are contradictory, the listener will adjust A’s value lower (or higher), meaning the listener will not regard A as truly being B; (3) Finally, the value of A should lie between the old information A and the new information B. Therefore, the pragmatic reasoning result of auxesis expressions should be positioned between the old information A and the auxesis value B (A < B), whereas the reasoning result for meiosis expressions should be positioned between the old information A and the meiosis value B (A > B). In addition, some psychological experiments have validated the rationality of relevance theory of hyperbolic expressions to a certain extent (Colston and Carreno 2020; Winter and Marghetis 2023), but there are few validations from a mathematical perspective.
3 A Construction of Bayesian Model for the Reasoning Process
Cognitive science indicates that humans possess the ability for Bayesian probabilistic reasoning (Oaksford and Chater 2009). Using the Bayesian model to conduct linguistic research fundamentally falls within the realm of probabilistic linguistics. This approach has five characteristics: (1) probability; (2) interactivity; (3) rationality and optimization; (4) computability; (5) data-driven. It takes into account the uncertainty that may be involved in language, which can be described using probabilities (Franke and Jäger 2016). The core concepts of Bayesian reasoning are prior and posterior. People make preliminary estimates about the development of an event based on experience, historical data, or imagination; this estimate is known as the prior, e.g., people may believe that “hot pot (a type of Chinese cuisine) is always spicy” based on experience. After personal experience or recounting by others, a new estimate is formed, termed the posterior, e.g., after tasting a tomato hot pot, one concludes that “hot pot can be spicy or sour.” The process of updating prior cognition with new data to form posterior cognition is referred to as the Bayesian process.
3.1 Bayesian Model for Semantic Reasoning: Conditional Probability
From a probabilistic standpoint, the event represented by a hyperbolic numerical idiom occurs with very low probability, and it can deduce idiomatic events with any other arbitrary quantity. In the Bayesian model context, the hyperbolic numerical idiom itself corresponds to prior events, while other events correspond to posterior events. Therefore, the question now involves whether prior events can infer posterior events. This reasoning process can be described using conditional probability. Conditional probability is a simpler form of the Bayesian model and refers to the probability of one event occurring given that another event has occurred.
Although in hyperbolic numerical idioms, the numbers do not represent exact meanings, this study still converts the numbers in the idioms into Arabic numerals for calculation. This is because the literal meaning of these numbers is sufficient for the expression to convey counterintuitive information. To calculate whether hyperbolic numerical idioms imply a relationship regarding quantity value, we can denote the probability function for the events represented by hyperbolic numerical idioms as p(x), where x represents the numerical value of the idiom. Thus, whether an expression with interval x2 can infer an expression with interval x1 can be calculated using the following formula:
Here,
Taking the hyperbolic numerical idiom 一毛不拔 (yī máo bù bá) as an example, this is a negative meiosis expression. Treating yī (one) as the numerical value “1,” we can calculate the conditional probability as follows:
3.2 Bayesian Model for Pragmatic Reasoning: Bayes’ Theorem
Building upon Grice’s foundational model of pragmatic reasoning, research in this area has flourished. Subsequent scholars have sought to employ mathematical methods to investigate pragmatic reasoning with greater precision and scientific rigor. However, formal models of pragmatic reasoning have encountered limitations, as they can only account for a subset of pragmatic phenomena and primarily rely on qualitative analyses. In response to this challenge, later researchers have proposed the Bayesian model of pragmatic reasoning, a probabilistic framework that is particularly suited for exploring vagueness in language, especially regarding complex and variable pragmatic phenomena that involve the listener’s cognition, context, and other factors (Goodman and Frank 2016). Given that listeners do not need to be aware of every detail within a conversation but can infer the speaker’s intention through associative information, the Bayesian model provides an accurate, quantitative tool for pragmatic reasoning based on relevant contextual cues. This model transforms the listener’s cognitive processes into computable probability functions, thereby simulating the information transmission process in communication (Frank and Goodman 2012). The probability function is subjective, as listeners may update their cognitive states based on the speaker’s ostensive expressions, leading to changes in this probability function over time (Lassiter 2011; Lassiter and Goodman 2017).
Research utilizing the Bayesian model for the pragmatic reasoning of hyperbolic numerical idioms has not received widespread attention. However, previous work on establishing a macroscopic Bayesian framework for pragmatic reasoning has gradually matured, allowing for comparative studies. Researchers such as Russell (2012), Frank and Goodman (2012), Goodman and Stuhlmüller (2013), Lassiter and Goodman (2013, 2017), Goodman and Frank (2016), Herbstritt and Franke (2019), Grove et al. (2021) and Tessler et al. (2022) have developed Bayesian models tailored to their respective research subjects, such as scalar implicatures reasoning, referential reasoning, and specific sentence structure reasoning, all relying on the speaker’s prior knowledge, context information, and ostensive expression to infer the listener’s pragmatic reasoning outcomes. In Chinese linguistic studies, the Bayesian approach to pragmatic reasoning has not been given adequate attention and remains in the preliminary exploration phase, with only a few studies such as those by Huang and Jiang (2011), Xiang and Liu (2022), Li (2023, 2024). Thus, there is an urgent need to conduct precise and scientific quantitative analyses of pragmatic reasoning phenomena in Chinese using the Bayesian model.
We need to focus on the distribution of parameters (denoted as θ) in the probability function p(x) of hyperbolic numerical idioms. Here, θ is associated with the listener’s quantity cognitive estimation, while other factors unrelated to the idiom need not be included as variables in the Bayesian model. Since p(x) contains the parameter θ, we can also express it as p(x∣θ). Let E(θ) denote the expectation of p(x∣θ), representing the mean of quantity estimation. Bayes’ theorem calculates the posterior distribution based on prior distributions and likelihood data:
Where π(θ) is the prior distribution, π(θ∣data) is the posterior distribution, and p(data∣θ) is the likelihood data. All the parameters on the right-hand side of the equation can be obtained from communicative information: (1) π(θ) is the probability distribution of the listener’s cognitive estimation of the event occurring normally, denoted as e1 for its expectation; (2) p(data∣θ) refers to the speaker’s ostensive expression information; (3) π(θ∣data) represents the new probability distribution after the listener updates their cognitive estimation of θ based on the ostensive expression. The expectation of posterior distribution π(θ∣data) can typically be regarded as the inferential outcome for θ, denoted as e2.
In summary, we can correspond the relevant parameters in the Bayesian model with relevant concepts in the ostensive-inferential model, as shown in Table 1. Here,
Analogous concepts in two reasoning theories.
| Bayesian inference | Ostensive inference |
|---|---|
|
|
Old information |
| data | New information |
|
|
Reasoning result |
This formula explores the position of the pragmatic reasoning result between old information A and new information B. The closer the Int value approaches 1, the greater the intensity of the reasoning.
For a practical illustration of Bayesian reasoning, consider the story of “The Boy Who Cried Wolf.” Certainly, as mentioned above, the setting of probabilities is subjective, but it must be close enough to the truth. Let π(θ) represent the probability that “villagers find the child trustworthy,” while
When the child first lies and says “the wolf is coming,” the posterior probability becomes:
4 Bayesian Inference Analysis of Four Types of Hyperbolic Numerical Idioms
This section will analyze the semantic and pragmatic reasoning of four types of hyperbolic numerical idioms using the Bayesian model from the previous section, and will discuss the reasoning results.
4.1 Affirmative Auxesis: yí chòu wàn nián (A Bad Reputation Will Last for Ten Thousand Years)
Semantic reasoning: The event represented by yí chòu wàn nián is an event with an extremely low probability, which is a prerequisite for initiating scalar reasoning. The scalar reasoning process of yí chòu wàn nián involves reasoning from large to small quantities, as shown in Figure 2. The expression yí chòu x nián forms a set of events that change with x, where the probability of the event p(x) not only has the characteristic of a monotonically decreasing function but also has the following conditional probability result:

Scalar reasoning of yí chòu wàn nián.
This conditional probability indicates that if a person’s bad reputation lasts for more than 10,000 years, it must also exceed 9,999 years. Consequently, it can be inferred that this person’s bad reputation lasts longer than any duration less than 10,000 years. Since wàn (ten thousand) is an auxesis quantity representing a significant point of cognitive recognition, and since any event less than this auxesis quantity holds, it follows that the auxesis can infer the totality, thereby validating Israel’s scalar reasoning rules.
Pragmatic reasoning: The duration of a person’s bad reputation follows the news effect, where popularity is high in the short term but quickly declines. Thus, it should obey an exponential distribution:
where x is a non-negative number, and
At this point, e1 = 1, thus
The posterior distribution π(θ∣data) is a gamma distribution with α = 3 and β = 10,002 (as shown in Figure 3). The expected value of this posterior distribution is calculated to be

Pragmatic reasoning of yí chòu wàn nián.
This indicates a significant difference between the listener’s prior and posterior cognition, suggesting that hyperbolic numerical idioms facilitate the occurrence of pragmatic reasoning.
4.2 Negative Meiosis: yī wén bù zhí (The Value is not Even Worth 1 Yuan)
Semantic reasoning: The event represented by yī wén bù zhí is an event with an extremely low probability, which is necessary for initiating scalar reasoning. The scalar reasoning process for yī wén bù zhí involves reasoning from small to large quantities, as shown in Figure 4. The expression x wén bù zhí forms a set of events that change with x, where the probability of the event p(x) not only has the characteristic of a monotonically increasing function but also has the following conditional probability result:
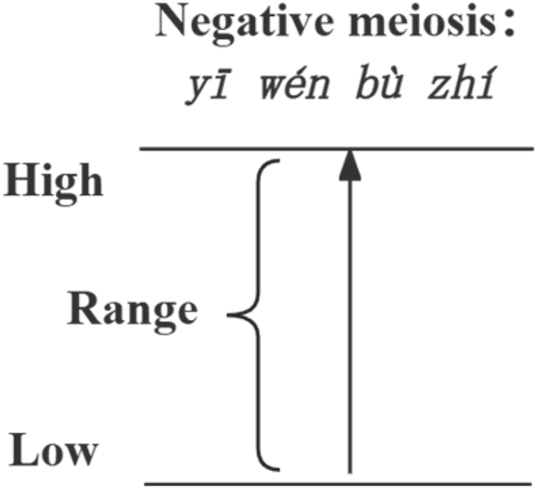
Scalar reasoning of yī wén bù zhí.
This conditional probability indicates that if the value of an item is “not exceeding 1 yuan,” it must also “not exceed 2 yuan,” and similarly, the value of the item “not exceeding any amount greater than 1 yuan” holds true. Since yī (one) is a meiosis quantity representing the smallest point of cognitive recognition, and any event greater than this meiosis quantity holds, it follows that the meiosis can infer the totality, thereby validating Israel’s scalar reasoning rules.
Pragmatic reasoning: The value of an item should follow a normal distribution, where most items’ values cluster in a certain range, while cheap and luxury items are relatively rare. We need to estimate the mean E(x|θ) = θ of the normal distribution, representing the average value of the item, while the standard deviation σ can be set as a constant, such as 10. Thus,
According to the 3-standard deviation rule of normal distribution, the value of the item mainly fluctuates within the interval [θ − 30, θ + 30]. Now we need to infer the changes in the listener’s cognition regarding θ. For the listener, the prior distribution of θ should also follow a normal distribution, as the mean value of an item’s worth can vary based on individual factors such as economic status and education level. We can set the prior distribution of θ to a normal distribution with a mean of 100 and a standard deviation of 10, thus e1 = 100:
The speaker’s expression yī wén bù zhí indicates that they have observed a data point of data = 1:
The posterior distribution π(θ∣data) is a normal distribution with a mean of
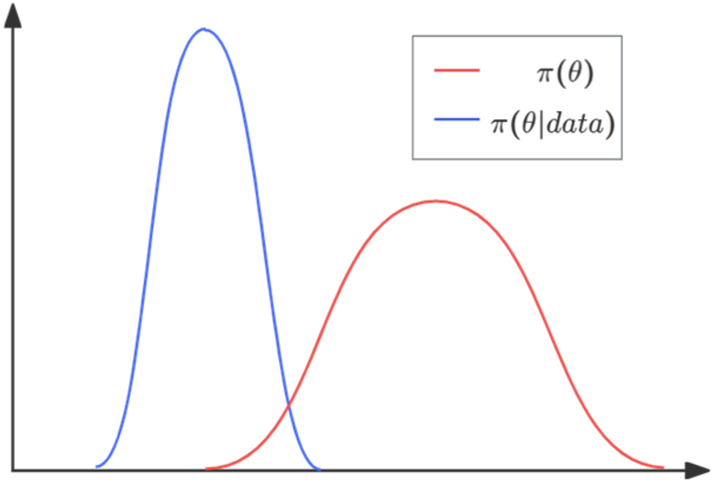
Pragmatic reasoning of yī wén bù zhí.
This indicates a significant difference between the listener’s prior and posterior cognition, suggesting that hyperbolic numerical idioms facilitate the occurrence of pragmatic reasoning.
4.3 Affirmative Meiosis: yī zhēn jiàn xiě (Only One Attack can Hit the Target)
Semantic reasoning: The event represented by yī zhēn jiàn xiě is an event with an extremely low probability, which is a prerequisite for initiating scalar reasoning. The scalar reasoning process for yī zhēn jiàn xiě involves reasoning from small to large quantities, as shown in Figure 6. The expression x zhēn jiàn xiě forms a set of events that change with x, where the probability of the event p(x) not only has the characteristic of a monotonically increasing function but also has the following conditional probability result:

Scalar reasoning of yī zhēn jiàn xiě.
This conditional probability indicates that if one attack can hit the target, then two attacks can also hit the target, and similarly, any number of attacks exceeding one can hit the target. Since yī (one) is a meiosis quantity representing the smallest point of cognitive recognition, and any event greater than this meiosis quantity holds, it follows that the meiosis can infer the totality, thereby validating Israel’s scalar reasoning rules.
Pragmatic reasoning: The number of attacks required to hit the target follows a geometric distribution:
where x is a positive integer, θ is the probability of hitting the target in one attack, and
At this point,
The posterior distribution π(θ∣data) is a Beta distribution with α = 2 and β = 10 (as shown in Figure 7), resulting in
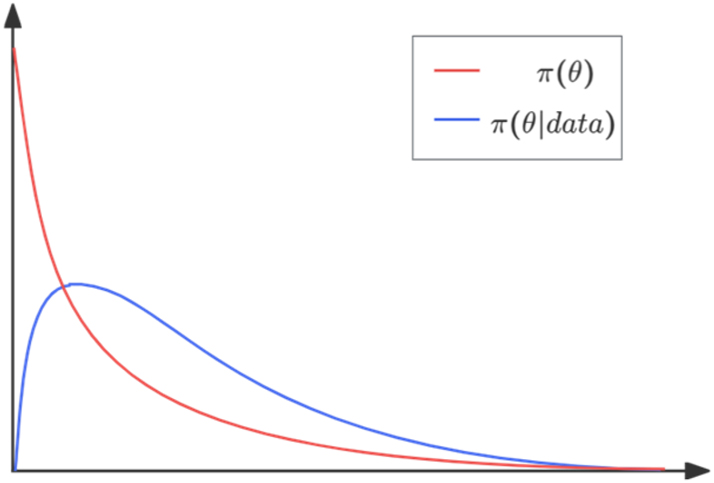
Pragmatic reasoning of yī zhēn jiàn xiě.
This indicates a significant difference between the listener’s prior and posterior cognition, suggesting that hyperbolic numerical idioms facilitate the occurrence of pragmatic reasoning.
4.4 Negative Auxesis: wàn sǐ bù cí (Willing to die Ten Thousand Times Without Hesitation)
Semantic reasoning: The event represented by wàn sǐ bù cí is an event with an extremely low probability, which is necessary for initiating scalar reasoning. The scalar reasoning process for wàn sǐ bù cí involves reasoning from large to small quantities, as shown in Figure 8. The expression x sǐ bù cí forms a set of events that change with x, where the probability of the event p(x) not only has the characteristic of a monotonically decreasing function but also has the following conditional probability result:

Scalar reasoning of wàn sǐ bù cí.
This conditional probability indicates that if a person can “die 10,000 times and not hesitate,” it must also include “dying 9,999 times and not hesitating.” Thus, it follows that a person can “not hesitate to die any number of times less than 10,000.” Since wàn (ten thousand) is an auxesis quantity representing a significant point of cognitive recognition, and since any event less than this auxesis quantity holds, it follows that the auxesis can infer the totality, thereby validating Israel’s scalar reasoning rules.
Pragmatic reasoning: The expression wàn sǐ bù cí means “a person dies 10,000 times without hesitation,” which should follow a binomial distribution:
where x is a non-negative integer, θ is the probability of “not hesitating after dying once,” and E(x|θ) = 10000θ represents the expected number of times “not hesitating” in 10,000 trials. We need to infer the changes in the listener’s cognition regarding θ. Assuming that in the listener’s prior cognition, “dying and not hesitating” is an extremely challenging task, the probability θ is larger when closer to 0 and smaller when closer to 1. We can set it as a Beta distribution with α = 1 and β = 10:
At this point,
The posterior distribution π(θ∣data) is a Beta distribution with α = 10,001 and β = 10 (as shown in Figure 9). The expected value of this posterior distribution is calculated to be
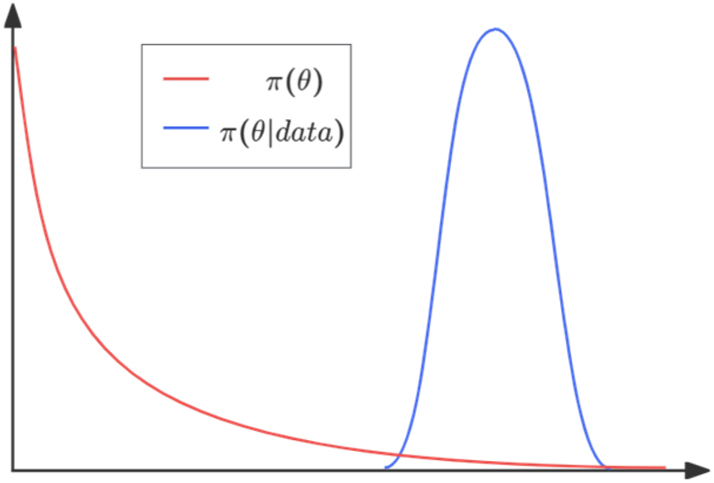
Pragmatic reasoning of wàn sǐ bù cí.
This indicates a significant difference between the listener’s prior and posterior cognition, suggesting that hyperbolic numerical idioms facilitate the occurrence of pragmatic reasoning.
5 Discussion
5.1 Common Characteristics of the Reasoning Process in Hyperbolic Numerical Idioms
In Sections 4, We analyzed four types of scalar reasoning and pragmatic reasoning of hyperbolic numerical idioms. The summary of the reasoning processes for the four types of idioms is presented in Table 2. Despite the differences among the four types, from a Bayesian perspective, they share common reasoning characteristics:
In terms of scalar reasoning, the conditional probability formulas demonstrated that hyperbolic quantities can infer total quantities, aligning with the theory of scalar reasoning. It is always possible to infer the opposite quantity from hyperbolic quantities, specifically, auxesis numerical idioms can infer expressions smaller than their quantities, while meiosis numerical idioms can infer expressions larger than their quantities.
In terms of pragmatic reasoning, Bayes’ theorem proved that hyperbolic numerical idioms significantly impact the listener’s cognition, hence the results of numerical cognition significantly shift from old information to new information, which is consistent with the ostensive-inferential model.
The directions of semantic reasoning and pragmatic reasoning are exactly opposite, which is precisely caused by the impossibility and counterfactuality of hyperbolic rhetoric.
Pragmatic reasoning patterns of hyperbolic numerical idioms.
| Hyperbolic numerical idiom | Bayesian pragmatic reasoning | Direction of semantic reasoning | Direction of pragmatic reasoning |
|---|---|---|---|
| Affirmative auxesis: yí chòu wàn nián | Prior expectation: 1 year Posterior expectation:3,334 years |
From large to small | From small to large |
| Negative meiosis: yī wén bù zhí | Prior expectation: 100 yuan Posterior expectation:50 yuan |
From small to large | From large to small |
| Affirmative meiosis: yī zhēn jiàn xiě | Prior expectation: 11 times Posterior expectation: 6 times |
From small to large | From large to small |
| Negative auxesis: wàn sǐ bù cí | Prior expectation: 909 times Posterior expectation:9,990 times |
From large to small | From small to large |
5.2 Applicability Analysis of Bayesian Models for Semantic and Pragmatic Reasoning
Based on the previous research findings, it can be observed that the Bayesian model offers certain advantages in reasoning research: (1) Bayesian theory is a branch of probability theory, and the mathematical research methods ensure that the findings are scientific, rigorous, and credible; (2) Probability theory focuses on the likelihood of events, while natural language conveys semantic and pragmatic information about events, therefore, employing the Bayesian model is suitable for natural language research, transforming concepts such as information quantity, modality, and cognition into computable values, accurately capturing the inferential relationships between events; (3) Bayesian theory excels at addressing issues involving many subjective factors in the reasoning process (such as individual experiences, dynamically changing contexts, and others), thereby breaking through the bottlenecks faced by formal semantics and formal pragmatics in resolving such issues to some extent. However, Bayesian models are not capable of resolving every detail in the reasoning process, and we should be aware of the following limitations:
In semantic reasoning research, Bayesian models can only explain the causal relationship between events with a conditional probability of 1, but not the reasoning relationship between events with probabilities not equal to 1. When the probability is not 1, there is a correlation between two events, but the degree of this correlation may have different meanings in different events, which may not be explained by Bayesian models.
In pragmatic reasoning research, we always need to design probability functions that conform to the actual situation of the event. However, since the listener and contextual information are quite complex, this probability function cannot be guaranteed to be applicable in every communicative situation. The probability function designed in the previous case analysis only holds true under normal circumstances. For some special communicative situations, other probability functions need to be designed to simulate the real situation as much as possible. However, as long as we can construct a prior distribution and likelihood data that align with the authentic communication situation, the resulting posterior distribution will necessarily conform to the pragmatic reasoning outcomes of the listener. We should not question the subjectivity of the probability distribution design presented in this paper, as the reasoning process of the listener itself is influenced by individual differences and contextual variations, which are unavoidable and inherently subjective. We advocate for obtaining the prior distribution, likelihood data, and posterior distribution through methods such as questionnaires and psychological experiments to validate the rationale of the research methods discussed in this paper. On the other hand, the prior and posterior expectations reflect maximal relevance rather than optimal relevance. Sperber and Wilson (1986: 118–171) strictly distinguish between maximal relevance and optimal relevance. In communication, since listeners cannot establish connections with all contexts within a limited time and are also unwilling to exert excessive effort, they pursue optimal relevance rather than maximal relevance. Although many scholars have pointed out the similarities between Bayesian theory and relevance theory, there has yet to be a thorough examination of whether Bayesian theory can also differentiate between maximal relevance and optimal relevance. In our case analysis, the posterior expectation represents the region of maximal or relatively large probability density, indicating maximal relevance, but the position of optimal relevance cannot be determined. In reality, the posterior distribution must contain optimal relevance, and the position of optimal relevance should be within a region of non-negligible probability density. Building on this research, we advocate for further studies on Bayesian interval estimation to calculate the areas where parameters fall around the posterior expectation with higher probability density (which can be set at 0.95 or 0.9). For instance, in Section 4.1, the idiom has the maximal relevance of 3,334 years, yet the posterior distribution indicates that the probability of a duration between 1,000 and 10,000 years exceeds 0.9, thereby sufficiently accommodating the optimal relevance, in any case, even the lowest value of 1,000 years far exceeds the prior expectation of 1 year, which indicates that the listener has made a relatively obvious pragmatic reasoning based on the hyperbolic expressions.
5.3 Strategic Study of Hyperbolic Numerical Idioms
This section discusses the applicable contexts for hyperbolic numerical idioms – specifically, which contexts favor the use of hyperbolic numerical idioms as optimal expressions and which contexts render them less effective. The effectiveness of expression strategies is determined by the results of semantic and pragmatic reasoning, with a primary focus on pragmatic reasoning. If Int is small, it indicates that the intensity of reasoning is weaker, hence it is a disadvantageous expression.
5.3.1 Optimal Strategies for Hyperbolic Numerical Idioms
Using 万死不辞 (wàn sǐ bù cí) and its derivative expressions as an example, we explore optimal expression strategies in different contexts.
| Question: |
|---|
| Comparing the pragmatic reasoning results of 万死不辞 (wàn sǐ bù cí) and 不推辞 (bù tuī cí) |
| Context: Diaochan, to repay Yun Wang’s kindness, decides to comply with Yun Wang’s request to offer herself to Bu Lü and Zhuo Dong, using different verbal strategies. |
| Diaochan’s strategy 1: 妾蒙大人恩养,训习歌舞,优礼相待,妾虽粉身碎骨,莫报万一。倘有用妾之处, 万死不辞 ! Qiè méng dà rén ēn yǎng, xùn xí gē wǔ, yōu lǐ xiāng dài, qiè suī fěn shēn suì gǔ, mò bào wàn yī. Tǎng yǒu yòng qiè zhī chù, wàn sǐ bù cí! I have been favored and nurtured by you, my Lord, trained in singing and dancing, treated with great courtesy. Even if I were to be shattered into pieces, I would have no way to repay you. If there is any use for me, I would not hesitate to die ten thousand times ! |
| Diaochan’s strategy 2: 妾蒙大人恩养,训习歌舞,优礼相待,妾虽粉身碎骨,莫报万一。倘有用妾之处, 妾身不辞 。 Qiè méng dà rén ēn yǎng, xùn xí gē wǔ, yōu lǐ xiāng dài, qiè suī fěn shēn suì gǔ, mò bào wàn yī. Tǎng yǒu yòng qiè zhī chù, qiè shēn bù cí. I have been favored and nurtured by you, my Lord, trained in singing and dancing, treated with great courtesy. Even if I were to be shattered into pieces, I would have no way to repay you. If there is any use for me, I would not hesitate . |
The pragmatic reasoning for strategy 1 wàn sǐ bù cí has been detailed in Section 4.4. On the other hand, Diaochan’s strategy 2 qiè shēn bù cí can be interpreted as conducting only one trial of “refusing or not refusing” (where E(x|θ) = θ), with the experimental result being “not refusing,” i.e., data = 1. The likelihood function can be expressed as:
Thus, the posterior distribution
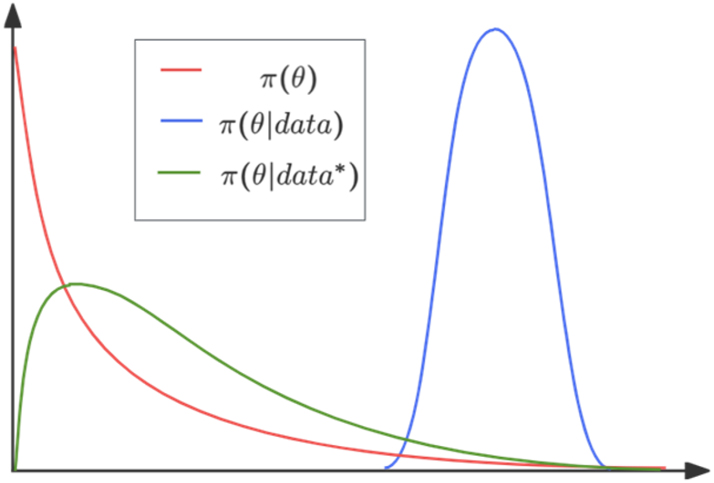
Probability comparison of hyperbolic expressions as optimal strategies.
This intensity is relatively weak and much lower than the pragmatic reasoning intensity of strategy 1 wàn sǐ bù cí, which is 0.99. Therefore, in this communicative context, strategy 1 wàn sǐ bù cí represents a more optimal strategy, better reflecting Diaochan’s determination.
5.3.2 Non-Dominant Strategies for Hyperbolic Expressions
Using the erroneous hyperbolic expression 万死推辞 (wàn sǐ tuī cí) and its derivative expressions as an example, we explore optimal expression strategies in different contexts.
| Question |
|---|
| Comparing the pragmatic reasoning results of 万死推辞 (wàn sǐ tuī cí) and 请恕推辞 (qǐng shù tuī cí) |
| Context: Master Wang instructs San Zhang to complete a difficult task, and San Zhang plans to refuse, using different verbal strategies. |
| San Zhang’s strategy 1: 晚辈从小胆小怕事, 请恕推辞 。 Wǎn bèi cóng xiǎo dǎn xiǎo pà shì, qǐng shù tuī cí. I have been timid and fearful since childhood; please forgive my refusal . San Zhang’s strategy 2: 晚辈从小胆小怕事, 万死也推辞 。 Wǎn bèi cóng xiǎo dǎn xiǎo pà shì, wàn sǐ yě tuī cí. I have been timid and fearful since childhood; even if I were to die ten thousand times, I would still refuse . |
San Zhang’s strategy 2 wàn sǐ tuī cí indicates “refusing even if one were to die ten thousand times,” thus it follows a binomial distribution:
where x is a non-negative integer, θ is the probability of “refusing even if one were to die once,” and E(x|θ) = 10000θ represents the expected number of times “refusing” in 10,000 trials. We now need to infer the changes in the listener’s cognition regarding θ. Assuming that in the listener’s prior cognition, “refusing even if one were to die” is an extremely easy task, the probability of θ is larger when closer to 1 and smaller when closer to 0. Given the known probability distribution from Section 4.4 for “dying and not refusing,” we can deduce that the probability distribution for “refusing even if one were to die” follows a Beta distribution with α = 10 and β = 1:
At this point,
Thus, the posterior expectation for strategy 2 wàn sǐ tuī cí is
Consequently, the pragmatic reasoning intensity for strategy 2 wàn sǐ tuī cí is calculated as:
Meanwhile, for strategy 1 qǐng shù tuī cí, the pragmatic reasoning intensity is:
The probability distribution is shown in Figure 11. We find that hyperbolic expression is not always the optimal form of communication in any context. Although the reasoning intensity of strategy 2 is high, the posterior expectation does not show a significant change in value compared to the prior expectation due to the narrow range of
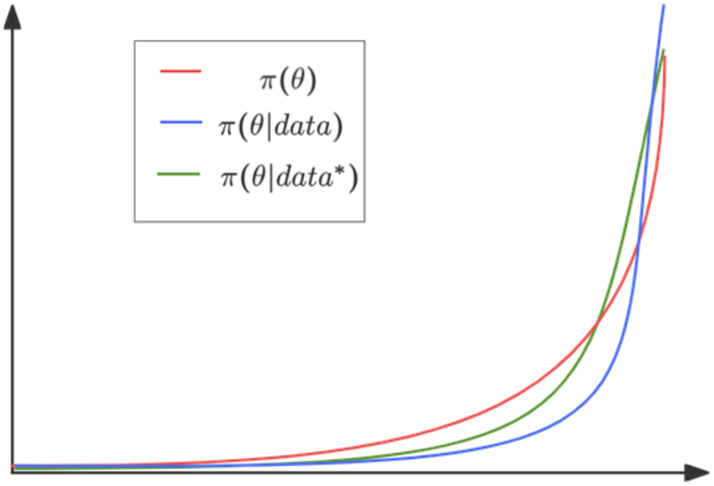
Probability comparison of hyperbolic expressions as non-dominant strategies.
6 Conclusions
This study takes Chinese hyperbolic numerical idioms as examples and employs Bayesian models to explore the operational mechanisms of semantic reasoning and pragmatic reasoning in hyperbolic rhetoric, thereby confirming previous theories of scalar reasoning and ostensive-inferential model. This research partially fills the theoretical gap in the phenomena of hyperbolic rhetoric in Chinese and provides a newer mathematical perspective. We look forward to conducting more research on cross-linguistic hyperbolic rhetoric from a Bayesian perspective.
Funding source: National Social Science Fund of China
Award Identifier / Grant number: 19BYY027
References
Bergen, L., R. Levy, and N. Goodman. 2016. “Pragmatic Reasoning through Semantic Inference.” Semantics and Pragmatics 9 (1): 1–91. article 20. https://doi.org/10.3765/sp.9.20.Search in Google Scholar
Carston, R. 1998. “Informativeness, Relevance, and Scalar Implicature.” In Relevance Theory: Applications and Implications, edited by Robyn Carston, and Seiji Uchida, 179–236. Amsterdam: John Benjamins Publishing Company.Search in Google Scholar
Carter, S. 2019. “The Dynamics of Loose Talk.” Noûs 55 (1): 171–98. https://doi.org/10.1111/nous.12306.Search in Google Scholar
Channell, J. M. 1983. Vague Language: Some Vague Expressions in English. Yorkshire: University of York, PhD Dissertation.Search in Google Scholar
Colston, H. L., and A. Carreno. 2020. “Sources of Pragmatic Effects in Irony and Hyperbole.” In Figurative Meaning Construction in Thought and Language, edited by Annalisa Baicchi, 187–208. Amsterdam: John Benjamins Publishing Company.Search in Google Scholar
Degen, J. 2023. “The Rational Speech Act Framework.” Annual Review of Linguistics 9 (1): 519–40, https://doi.org/10.1146/annurev-linguistics-031220-010811.Search in Google Scholar
Frank, M. C., and N. D. Goodman. 2012. “Predicting Pragmatic Reasoning in Language Games.” Science 336 (6084): 998. https://doi.org/10.1126/science.1218633.Search in Google Scholar
Franke, M., and G. Jäger. 2016. “Probabilistic Pragmatics, or Why Bayes’ Rule Is Probably Important for Pragmatics.” Zeitschrift für Sprachwissenschaft 35 (1): 3–44.Search in Google Scholar
Goodman, N. D., and M. C. Frank. 2016. “Pragmatic Language Interpretation as Probabilistic Inference.” Trends in Cognitive Sciences 20 (11): 818–29. https://doi.org/10.1016/j.tics.2016.08.005.Search in Google Scholar
Goodman, N. D., and A. Stuhlmüller. 2013. “Knowledge and Implicature: Modeling Language Understanding as Social Cognition.” Topics in Cognitive Science 5 (1): 173–84. https://doi.org/10.1111/tops.12007.Search in Google Scholar
Grove, J., J. P. Bernardy, and S. Chatzikyriakidis. 2021. “From Compositional Semantics to Bayesian Pragmatics via Logical Inference.” In Proceedings of the 1st and 2nd Workshops on Natural Logic Meets Machine Learning, 60–70.Search in Google Scholar
Herbstritt, M., and M. Franke. 2019. “Complex Probability Expressions & Higher-Order Uncertainty: Compositional Semantics, Probabilistic Pragmatics & Experimental Data.” Cognition 186 (5): 50–71, https://doi.org/10.1016/j.cognition.2018.11.013.Search in Google Scholar
Horn, L. R. 1996. “Presupposition and Implicature.” In The Hand Book of Contemporary Semantic Theory, edited by Shalom Lappin, 299–319. Oxford: Blackwell Publishers.Search in Google Scholar
Hsiao, C., and L. I. Su. 2010. “Metaphor and Hyperbolic Expressions of Emotion in Mandarin Chinese Conversation.” Journal of Pragmatics 42 (5): 1380–96. https://doi.org/10.1016/j.pragma.2009.09.006.Search in Google Scholar
Huang, Z., and Y. Jiang. 2011. “Bayesian Probability Models and Their Applications in Pragmatics.” In Approaching Formal Pragmatics, edited by Y. Jiang, 457–99. Shanghai: Shanghai Educational Publishing House.Search in Google Scholar
Israel, M. 2001. “Minimizers, Maximizers and the Rhetoric of Scalar Reasoning.” Journal of Semantics 18 (4): 297–331. https://doi.org/10.1093/jos/18.4.297.Search in Google Scholar
Israel, M. 2011. The Grammar of Polarity: Pragmatics, Sensitivity, and the Logic of Scales. Cambridge: Cambridge University Press.Search in Google Scholar
Jiang, Y. 2004. “The Scalar Implicature Function of Hyperbolic Metaphors.” Modern Foreign Languages 27 (3): 274–81.Search in Google Scholar
Jiang, Y. 2010. “The Probability-Based Scalar Model of Polarity Items.” In Editorial Board of the Journal of Language Studies, Department of Chinese Philology, Bulletin of Linguistic Studies Vol. 7, edited by Fudan University, 95–108. Shanghai: Shanghai Lexicographical Publishing House.Search in Google Scholar
Jiang, Y., and W. Gong. 2006. “Supplements to the Scalar Model of Polarity Items.” Modern Foreign Languages 29 (1): 10–9.Search in Google Scholar
Jiang, Y., and T. Xu. 2024. “The Scalar Rhetorical Function of Numerical Maximizers and Minimizers in Idioms: An Interdisciplinary Study of Rhetoric, Probability Theory, and Information Theory.” Contemporary Rhetoric 43 (6): 66–79.Search in Google Scholar
Kann, A. 2022. For the Fifty-Eleventh Time": Examining Cross-Linguistic Properties of Hyperbolic Numerals and Quasi-Numeral Expressions through Parallel Text Extraction. Stockholm: Stockholm University Master Thesis.Search in Google Scholar
Kennedy, C. 2007. “Vagueness and Grammar: The Semantics of Relative and Absolute Gradable Adjectives.” Linguistics and Philosophy 30 (1): 1–45, https://doi.org/10.1007/s10988-006-9008-0.Search in Google Scholar
Krifka, M. 2007. “Approximate Interpretations of Number Words: A Case for Strategic Communication.” In Cognitive Foundations of Interpretation, edited by Gerlof Bouma, Irene Krämer, and Joost Zwarts, 111–26. Amsterdam: Royal Netherlands Academy of Arts and Sciences.Search in Google Scholar
Lassiter, D. 2011. “Vagueness as Probabilistic Linguistic Knowledge.” In Vagueness in Communication, edited by Rick Nouwen, 127–50. Berlin, Heidelberg: Springer.Search in Google Scholar
Lassiter, D., and N. D. Goodman. 2013. “Context, Scale Structure, and Statistics in the Interpretation of Positive-form Adjectives.” In Proceedings of SALT, Vol. 23, 587–610. https://doi.org/10.3765/salt.v23i0.2658.Search in Google Scholar
Lassiter, D., and N. D. Goodman. 2017. “Adjectival Vagueness in a Bayesian Model of Interpretation.” Synthese 194 (10): 3801–36, https://doi.org/10.1007/s11229-015-0786-1.Search in Google Scholar
Lauer, S. 2012. “On the Pragmatics of Pragmatic Slack.” In Proceedings of sinn und bedeutung, 389–402.Search in Google Scholar
Lavric, E. 2010. “Hyperbolic Approximative Numerals in Cross-Cultural Comparison.” In New Approaches to Hedging, edited by Gunther Kaltenböck, 123–64. Leiden: Brill.Search in Google Scholar
Li, X. 2023. A Study of Conversational Implicature-Computing Models and Applications Based on Bayesian Theories. Shanghai: East China Normal University PhD Dissertation.Search in Google Scholar
Li, X. 2024. “Computational Pragmatic Models for Cultural Pragmatic Inference.” Journal of Tianjin Foreign Studies University 31 (4): 43–54.Search in Google Scholar
Lyons, J. 1977. Semantics, Vol. 2. Cambridge: Cambridge University Press.Search in Google Scholar
Mao, S., and Y. Tang. 2012. Bayesian Statistics. Beijing: China Statistics Press.Search in Google Scholar
McCarthy, M., and R. Carter. 2004. ““There’s Millions of Them”: Hyperbole in Everyday Conversation.” Journal of Pragmatics 36 (2): 149–84, https://doi.org/10.1016/s0378-2166-03-00116-4.Search in Google Scholar
Mey, J. L. 1993. Pragmatics: An Introduction. Blackwell: Oxford.Search in Google Scholar
Oaksford, M., and N. Chater. 2009. “Précis of Bayesian Rationality: The Probabilistic Approach to Human Reasoning.” Behavioral and Brain Sciences 32 (1): 69–84. https://doi.org/10.1017/s0140525x09000284.Search in Google Scholar
Ran, Y. 2010. “Approximative Expressions and Their Loose Uses in Chinese.” In New Approaches to Hedging, edited by Kaltenböck Gunther, 165–80. Leiden: Brill.Search in Google Scholar
Russell, B. 2012. Probabilistic Reasoning and the Computation of Scalar Implicatures. PhD dissertation. Brown University. Providence.Search in Google Scholar
Sperber, D., and D. Wilson. 1986. Relevance: Communication and Cognition. Cambridge: Harvard University Press.Search in Google Scholar
Tessler, M. H., J. B. Tenenbaum, and N. D. Goodman. 2022. “Logic, Probability, and Pragmatics in Syllogistic Reasoning.” Topics in Cognitive Science 14 (3): 574–601. https://doi.org/10.1111/tops.12593.Search in Google Scholar
Verschueren, J. 1999. Understanding Pragmatics. London: Arnold.Search in Google Scholar
Wang, G., J. Shu, and L. Wang. 2024. “Diachronic Changes of Number Use in Written American English from 1923 to 2008.” Language Sciences 105 (5): 101656, https://doi.org/10.1016/j.langsci.2024.101656.Search in Google Scholar
Winter, B., and T. Marghetis. 2023. “Multimodality Matters in Numerical Communication.” Frontiers in Psychology 14 (1): 1130777, https://doi.org/10.3389/fpsyg.2023.1130777.Search in Google Scholar
Wu, Z., and X. Dai. 2009. “The Logical Meaning and Pragmatic Meaning of Numerals.” Language Teaching and Linguistic Studies 31 (1): 57–64.Search in Google Scholar
Xiang, M., and X. Liu. 2022. “Economic Approach towards Linguistics Studies: A Game-Theoretic Account of Lexical Blocking.” Journal of Shanghai Jiaotong University (Philosophy and Social Sciences) 30 (6): 110–9.Search in Google Scholar
Xu, C., and X. Yan. 2023. “An Epistemic Game-Theoretic Pragmatics Account of Linguistic Metaphors.” Studies in Logic 16 (2): 1–15.Search in Google Scholar
Yeom, J. I. 2006. “Numerals and Pragmatic Interpretations.” Language and Information 10 (2): 47–65. https://doi.org/10.29403/li.10.2.3.Search in Google Scholar
Zhang, Y. 2020. A Research on the Subjective Quantitative Semantics of the Idioms and Idiomatic Expressions with Numbers from the Perspective of Cognitive Linguistics. PhD dissertation. Xi’an: Shaanxi Normal University.Search in Google Scholar
© 2025 the author(s), published by De Gruyter on behalf of Shanghai International Studies University
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Frontmatter
- Research Articles
- Research on the Semantic and Pragmatic Reasoning of Chinese Hyperbolic Numerical Idioms Based on the Bayesian Model
- Compilation and Analysis of a Parallel English-Arabic Corpus of Stand-Up Comedy Shows Subtitles
- Stance Markers in Industry Report: A Corpus-Based Study of the Deloitte Art & Finance Report
- The Reception of Auteurs: Data Mining Reviews of Wes Anderson’s Films
- Balanced or Biased? Voice Engagement in Australian News Media’s Communication of China
- Differences in Journal Paper Titles between Natural Sciences and Humanities: A Corpus-based Analysis
- Mental Distress in English Posts from r/AmITheAsshole Subreddit Community with Language Models
- Modelling Differences in Multiword Expression Use Across Proficiency Levels in a Test of Spoken English
- Book Reviews
- Di Cristofaro, M: Corpus Approaches to Language in Social Media
- L. S. Ming and C. Sin-wai: Applying Technology to Language and Translation
Articles in the same Issue
- Frontmatter
- Research Articles
- Research on the Semantic and Pragmatic Reasoning of Chinese Hyperbolic Numerical Idioms Based on the Bayesian Model
- Compilation and Analysis of a Parallel English-Arabic Corpus of Stand-Up Comedy Shows Subtitles
- Stance Markers in Industry Report: A Corpus-Based Study of the Deloitte Art & Finance Report
- The Reception of Auteurs: Data Mining Reviews of Wes Anderson’s Films
- Balanced or Biased? Voice Engagement in Australian News Media’s Communication of China
- Differences in Journal Paper Titles between Natural Sciences and Humanities: A Corpus-based Analysis
- Mental Distress in English Posts from r/AmITheAsshole Subreddit Community with Language Models
- Modelling Differences in Multiword Expression Use Across Proficiency Levels in a Test of Spoken English
- Book Reviews
- Di Cristofaro, M: Corpus Approaches to Language in Social Media
- L. S. Ming and C. Sin-wai: Applying Technology to Language and Translation

