Abstract
There has been a considerable surge of experimental inquiry in recent years into understanding the factors responsible for the corrosion inhibition efficiency of chalcones; however, the question of what actually determines the efficiency still remains a topic of debate. In this study, the dependence of the inhibition effect of such two compounds, namely, 3-(3-oxo-3-phenyl-propenyl)-1H-quinolin-2-one and 3-(3-oxo-3-phenyl-propenyl)-1H-benzoquinolin-2-one, on their molecular and electronic structure is analyzed using density functional theory calculations. In agreement with experiments, this study found strong evidence to link corrosion inhibition property of the compounds to their actual molecular structures in acidic media.
1 Introduction
Despite perpetual development of new materials, steel is still one of the most reliable, most used, and most substantial materials of today. Depending on the chemical composition and the thermomechanical processing history during the manufacturing process, its mechanical properties can vary tremendously, covering an extensive range of strength, toughness, and ductility. Carbon steels are widespread materials because of the possibility to induce in them, by means of rapid quenching, an extremely hard phase: martensite. Although such steels show high mechanical properties and moderate corrosion resistance, their performance is reduced under aggressive environments due to a synergistic effect between wear and corrosion mechanisms (Tkalcec, 2004).
The concept of placing a protective barrier between materials and their environment is so ancient that its origin is lost in the mists of time. The best way to combat metal corrosion is by using inhibitors (Gerengi, Goksu, & Slepski, 2014; Palou, Xomelt, & Likhanova, 2014). Not much has actually been achieved using natural products, compared to the extensive research on organic inhibitors, particularly N- and S-containing organic compounds (Gece, 2011). In this regard, quinoline chalcones, which belong to the largest class of plant secondary metabolites that serve in plant defense mechanisms (Yaylı et al., 2004), seem to be rewarding, albeit their use is still restrained in the field of corrosion protection.
Ayyannan, Karthikeyan, Vivekananthan, Gopiraman, and Rathinavelu (2013) have recently reported remarkable inhibition efficiencies of two such compounds, i.e. 3-(3-oxo-3-phenyl-propenyl)-1H-quinolin-2-one (PPQ) and 3-(3-oxo-3-phenyl-propenyl)-1H-benzoquinolin-2-one (PPBQ) (Figure 1), for high carbon steel corrosion in HCl media. The results of their electrochemical and chemical measurements revealed that both compounds reduce the corrosion rate of high carbon steel to a large extent in HCl medium. The inhibition efficiency of PPBQ reached up to about 95%, a little bit higher rate than that of PPQ (∼93%), at a concentration of 400 ppm. Furthermore, detailed analysis of steel surface by spectroscopic methods suggested a relatively vigorous adsorption of these inhibitors through the C=O and N-H groups.

Molecular structure of (A) PPQ and (B) PPBQ.
Although their experimental work has shown that the inhibitor molecules act by adsorption at the metal/solution interface, the degree to which direct relationships exist between inhibition efficiency and structural/electronical features of these inhibitors is still uncertain. Quantum chemical calculations are proving to be increasingly valuable in providing insights regarding how structure and substituents modulate the inhibition properties (Gece, 2008).
Propelled by the recent understanding of the role of density functional theory (DFT) calculations in corrosion inhibitor research (Awad, Metwally, Soliman, El-Zomrawy, & Bedair, 2014; Gece, 2008, 2013; Khadom, 2013; Obot & Gasem, 2014; Obot, Macdonald, & Gasem, 2015; Udhayakala, 2015; Zarrouk et al., 2013), in this work, it is aimed at addressing the need for a better understanding of how inhibition mechanisms of these compounds work and why PPBQ prevails slightly over the inhibition effect of PPQ.
2 Computational methods
All calculations have been performed with the Gaussian 09 suite of programs (Frisch et al., 2009). The ground-state geometry of each compound has been fully optimized with default thresholds using the standard triple split valence basis set supplemented by polarization and diffuse functions 6-311++G(d,p) basis set. Subsequently, vibrational frequencies were calculated analytically at the same level of theory as in the previous step to verify the optimized structure. The DFT calculations were carried out in the framework of the Becke-Lee-Yang-Parr (B3LYP) functionals, in which the exchange functional is a local spin density exchange with the Becke gradient correction and the correlation functional is that of Lee, Yang, and Parr with both local and nonlocal terms. The phenomenon of electrochemical corrosion takes place in the liquid phase, so it is relevant to include the effect of solvent in the computations. Self-consistent reaction field (SCRF) theory with Tomasi’s polarized continuum model (PCM) was used to perform the calculations in solution. These methods model the solvent as a continuum of uniform dielectric constant (ε=78.5) and define the cavity where the solute is placed as a uniform series of interlocking atomic spheres.
3 Results and discussion
The molecular structure of quinoline chalcones is composed of two aromatic rings joined by a three-carbon α,β-unsaturated carbonyl segment. One of the rings is a propiophenone, and the second ring is a quinolinone (Figure 1). Recorded pharmacological studies with such compounds in which the relative position of electron-releasing groups in the aromatic rings is modified are profuse (Berar, 2012). Recent research on the geometric parameters of different substituted quinoline chalcones by Xue et al. (2011), which explicitly brings the effects of the introduction of substituents into the analysis along with the increase in conjugate chain length, indicates that the relationship between the structure and the elongation of the conjugate chain is indeed entirely weak. Apart from this clue, the question of whether the extra benzene ring in PPBQ accounts for its higher inhibition compared to that of PPQ can be addressed first through an accurate description of the geometric structures of these compounds. As the experimental data used in this study were predicated on the results of electrochemical measurements in 10% HCl solution (Ayyannan et al., 2013), at this point it is necessary to disambiguate the exact condition of the compounds in such a strong acidic medium. It has been reported that chalcone-type compounds are subject to structural transformations in aqueous solutions in parallel with pH changes (Pina, Maestri, & Balzani, 1999).
The flavylium cations of PPQ and PPBQ, as can be seen in Figure 2, are supposed to be the most thermodynamically stable forms below pH 3. Thus, it will be necessary to ensure that calculations are extended to take account of the protonated forms of these inhibitors. The B3LYP/6-311++G(d,p) fully optimized structures of neutral and protonated forms of PPQ and PPBQ are illustrated in Figure 3. To validate the DFT-optimized geometries of the compounds, some selected parameters are listed in Table 1, with reference atom numbering given in Figure 3, and have been compared to those obtained experimentally for the crystal structure of chalcone (Rabinovich, 1970).
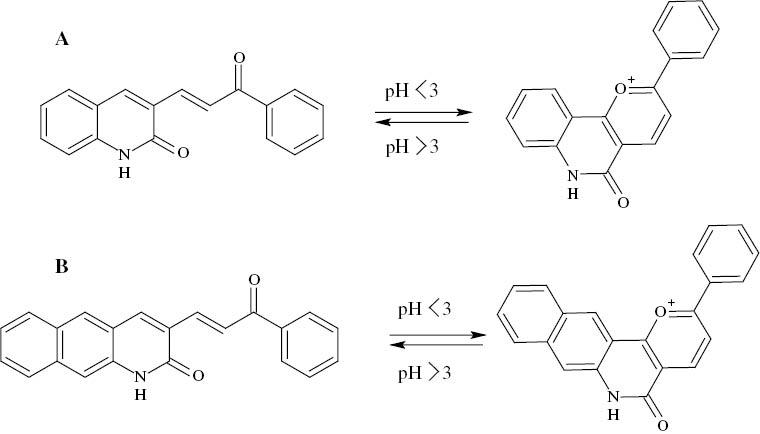
Structural transformation of (A) PPQ and (B) PPBQ in strong acidic medium.

Optimized structures at the B3LYP/6-311++G(d,p) level for the neutral and protonated forms of (A) PPQ and (B) PPBQ in the aqueous phase.
Selected geometric parameters for neutral forms of PPQ and PPBQ (for atom numbering scheme, please see Figure 3).
| Inhibitor | Parameters | DFTa | Exp.b | Inhibitor | Parameters | DFTa | Exp.b |
|---|---|---|---|---|---|---|---|
| PPQ | Bond lengths (Å) | PPBQ | Bond lengths (Å) | ||||
| C23-C21 | 1.503 | 1.500 | C21-C19 | 1.503 | 1.500 | ||
| C21-O22 | 1.225 | 1.205 | C19-O20 | 1.233 | 1.205 | ||
| C21-C20 | 1.486 | 1.479 | C19-C18 | 1.485 | 1.479 | ||
| C20-C18 | 1.347 | 1.320 | C18-C16 | 1.352 | 1.320 | ||
| C18-C12 | 1.452 | 1.465 | C16-C10 | 1.454 | 1.465 | ||
| Bond angles (°) | Bond angles (°) | ||||||
| C25-C23-C21 | 117.7 | 117.6 | C22-C21-C19 | 123.5 | 117.6 | ||
| C23-C21-O22 | 119.9 | 120.4 | C21-C19-O20 | 119.9 | 120.4 | ||
| O22-C21-C20 | 121.2 | 121.1 | O20-C19-C18 | 121.1 | 121.1 | ||
| C21-C20-C18 | 119.6 | 120.4 | C19-C18-C16 | 119.6 | 120.4 | ||
| C20-C18-C12 | 128.3 | 127.6 | C18-C16-C10 | 128.3 | 127.6 | ||
| C18-C12-C13 | 121.8 | 118.4 | C16-C10-C11 | 121.9 | 118.4 |
aCalculated values at the B3LYP/6-311++G(d,p).
bX-ray data from Xue et al. (2011).
The dihedral angle of the PPQ molecule between C21 and C26 atoms is about 177°, corresponding to a transoid conformational type, whereas PPBQ has a cisoid conformation that is stabilized by π-π overlap across the planar quinolinone rings of the molecule. Bond lengths and angles found for the neutral form of PPQ do not deviate much from the values for the neutral form of PPBQ. The length of C=O bonds is in agreement with the length of a typical carbonyl double bond (∼1.24 Å) (Pyykkö & Atsumi, 2009). Because of the position of this oxygen, the repulsion experienced by the propiophenone ring when coplanar with the central part is greater than that experienced by the oxo-quinoline ring, and accordingly the stabilising and repulsive forces between the quinolinone ring and the carbonyl segment are more closely balanced.
It appears from Table 1 that the C25-C23-C21 angle of PPQ (117.7°) is shorter than that of the corresponding angle of PPBQ (123.5°) due to the same reasons. Furthermore, all carbon-carbon single-bond lengths of PPQ and PPBQ are shorter than the common carbon-carbon single bond (1.54 Å) (Pauling, 1960), in contrast with the α-β carbon bond length (i.e. C20-C18 and C18-C16 lengths of PPQ and PPBQ, respectively), which shows mainly a double-bond character (∼1.35 Å) due to the partial delocalization of the π electrons. In spite of the minor differences, calculated geometric parameters represent a good approximation and can provide a starting point to calculate other parameters, such as the energies of the frontier molecular orbitals, as will be described below.
The inhibition effect of inhibitor compound is usually ascribed to adsorption of the molecule on the metal surface (Gece, 2008). If molecules adsorb at solid surfaces, this can occur either by chemical or by physical bonding. A chemical interaction can be analyzed from the starting point of the energy levels of the interacting fragments or molecules. In general, it often turns out that the highest occupied molecular orbital (HOMO), or a small subset of higher-lying levels, and the lowest unoccupied molecular orbital (LUMO), or some subset of unoccupied molecular orbitals, dominate the interaction between two molecules. These are called the frontier orbitals. They are the valance orbitals of the molecule, the orbitals most easily perturbed in any molecular interaction. The frontier orbital concept states that the reaction between two reactants takes place where the overlap of HOMO and LUMO is maximized (Fukui, 1982).
The HOMO density is closely related to the charge transfer (nucleophilic reactant), whereas for an acceptor compound, the LUMO density is important (electrophilic reactant). A high value of the HOMO energy corresponds to copious donation of electrons to congruent molecules with low-energy, empty molecular orbitals. Increasing values of EHOMO lead to an increment in adsorption and exalt the efficiency of inhibition. The energy of the LUMO indicates the ability of the molecule to accept electrons. The lower is the value of ELUMO, the more probable it is that the molecule would accept electrons (Awad et al., 2014; Gece, 2008, 2013; Khadom, 2013; Obot & Gasem, 2014; Obot et al., 2015; Udhayakala, 2015; Zarrouk et al., 2013). The HOMO-LUMO gap (ΔE), i.e. the difference in energy between the HOMO and LUMO, is used as a direct indicator of kinetic stability. A large HOMO-LUMO gap implies high kinetic stability and low chemical reactivity because it is energetically unfavorable to add electrons to a high-lying LUMO or to extract electrons from a low-lying HOMO. As the energy gap between the frontiers orbitals get smaller, the interactions between the reacting species get stronger (Gece, 2008).
In addition to these aspects, chemical hardness (η) is another important quantity in chemical reactivity theory and is a measure of the resistance of a chemical species to change its electronic configuration. The chemical hardness and electronegativity can be defined by using Koopmans’ theorem (Koopmans, 1934), which provides an easy method to calculate the ionization potential (I) and electron affinity (A) through orbital energies of optimized neutral molecules.
According to this theorem, the negative of the HOMO energy (-EHOMO) and the LUMO energy (-ELUMO) corresponds to ionization potential and electron affinity, respectively (i.e. I=-EHOMO and A=-ELUMO). The chemical hardness (η), electronegativity (χ), and chemical potential (μ) are thereby defined as
That is, the energy gap between the HOMO and LUMO is equal to 2η, and χ is halfway between the HOMO and LUMO. The frontier molecular orbital distributions of PPQ and PPBQ are shown in Figure 4. Whereas the HOMOs in both molecules are essentially composed of the oxo-quinoline ring π orbitals, the LUMOs feature important contributions from the oxygen atoms of the carbonyl group in addition to the ring system. In protonated PPQ, the HOMO is distributed over all three rings, whereas it is located only at the flavone benzopyrone ring in protonated PPBQ. However, although the LUMO is evenly distributed over all rings in protonated PPQ, it is more heavily localized on the flavylium phenyl ring in protonated PPBQ. This observation visually confirms why there are significant differences in EHOMO or ELUMO of protonated species.

Plots of the HOMO and LUMO orbital distribution for (A) neutral PPQ, (B) protonated PPQ, (C) neutral PPBQ, and (D) protonated PPBQ calculated by B3LYP/6-311++G(d,p).
All of the above explanations are pointing toward the exigency of comparing the electronic properties of PPQ and PPBQ. Certain quantum chemical parameters related to the molecular electronic structures of the compounds, such as EHOMO, ELUMO, and ΔE, have been used for the sake of comparison.
According to the data given in Table 2, the highest EHOMO and the lowest ELUMO and ΔE values are found for the neutral form of PPBQ molecule in both gas and aqueous phases. It is interesting to note that the protonated form of the PPBQ molecule in the aqueous state has the highest EHOMO and the lowest ELUMO and ΔE values when the data for the protonated form of the PPQ molecule were compared. This suggests that the dominant form responsible for the inhibition efficiency of PPBQ is its protonated form in acidic medium. These are accordant with experimental results (Ayyannan et al., 2013).
The calculated quantum chemical descriptors at the B3LYP/6-311G++(d,p) basis set for PPQ and PPBQ in gas and aqueous phases.
| Compound | Phasea | E HOMO (eV) | E LUMO (eV) | ΔE (EL–EH) (eV) | μ (D) | χ | η | ΔN | IE% b |
|---|---|---|---|---|---|---|---|---|---|
| Neutral | |||||||||
| PPQ | G | −6.418 | −2.732 | 3.686 | 4.879 | 4.58 | 1.84 | 0.02 | 91.9 |
| A | −6.478 | −2.744 | 3.734 | 6.608 | 4.61 | 1.87 | 0.02 | ||
| PPBQ | G | −6.207 | −2.843 | 3.364 | 5.062 | 4.53 | 1.68 | 0.04 | 93.6 |
| A | −6.078 | −2.928 | 3.150 | 7.672 | 4.50 | 1.58 | 0.05 | ||
| Protonated | |||||||||
| PPQ | G | −10.024 | −7.062 | 2.962 | 3.191 | 8.54 | 1.48 | −1.31 | |
| A | −7.062 | −3.917 | 3.145 | 3.260 | 5.49 | 1.57 | −0.26 | ||
| PPBQ | G | −9.219 | −6.917 | 2.302 | 4.104 | 8.07 | 1.15 | −1.48 | |
| A | −6.505 | −3.921 | 2.584 | 4.828 | 5.21 | 1.29 | −0.21 | ||
aG, gas phase (ε=1.0); A, aqueous phase (ε=78.5).
bAverage experimental value from Ayyannan et al. (2013).
Dipole moment of the compound is another parameter that predicts the polarized nature of the molecule, although its relation to inhibition efficiency is controversial. A very significant dipole moment may polarize the molecule in such a way that it produces a required potential at several atomic centers necessary for adsorption. It has been generally asserted that the efficiency of the inhibitor increases with the growth in the total dipole moment of the compound (Awad et al., 2014; Gece, 2008, 2013; Khadom, 2013; Obot & Gasem, 2014; Obot et al., 2015; Udhayakala, 2015; Zarrouk et al., 2013). The theoretical study has shown that neutral and protonated forms of PPBQ have the highest values of dipole moments compared to those obtained for PPQ in both gas and aqueous phases (Table 2).
Another concept in chemical reasoning about molecular behavior and reactivity of corrosion inhibitors are atomic charges and charge transfer. The published literature shows a tremendously large number of studies where atomic charges were found to be very instructive in interpreting the active centers of organic molecule responsible for interaction with metals (Gece, 2008). It has been documented that the higher magnitude and the number of negatively charged heteroatom present in an inhibitor molecule, the higher is its ability to be adsorbed on the metal surface via a donor-acceptor type reaction (Awad et al., 2014; Gece, 2008, 2013; Khadom, 2013; Obot & Gasem, 2014; Obot et al., 2015; Udhayakala, 2015; Zarrouk et al., 2013). Mulliken atomic charges for protonated forms of PPQ and PPBQ are shown in Figure 5. It is clear that the electron density on the flavylium oxygen cation of PPBQ (0.151 e) is slightly higher than that on the cation of PPQ (0.141 e). The negative charge on the nitrogen atom of PPQ (−0.159 e) is also lower compared to that of PPBQ (−0.170 e). On the other hand, it is observed that the negative values on the carbon atoms of the naphthalene ring system in PPBQ lead to a redistribution of electron density. Because of these strong negative charges, the carbon atoms of the flavylium ring where the nitrogen atom is connected accommodate higher positive charges and become more acidic.

Atomic Mulliken charges for the protonated forms of (A) PPQ and (B) PPBQ in the aqueous phase.
These findings have been further confirmed by calculating the fraction of electrons (ΔN) transferred from inhibitors to iron. When two systems, Fe and inhibitor, are brought together, electrons will flow from lower χ (inhibitor) to higher χ (Fe), until the chemical potentials become equal. Then, the ΔN value can be calculated according to Eq. (3).
where a global hardness of ηFe≈0 is accepted due to the extremely small number. The work function of Fe (4.67 eV) was used to represent the theoretical value of χFe (Lide, 2004). From Table 2, it is possible to observe that the protonated form of PPBQ has lower global hardness values. In general, the fraction of transferred electrons is also the largest for PPBQ. ΔN values showed that the inhibition efficiency resulting from electron donation is in accordance with Lukovits’ study (Lukovits, Kalman, & Zucchi, 2001). If ΔN<3.6, the inhibition efficiency increases by increasing electron-donating ability to the metal surface. Therefore, according to a series of properties calculated for each molecule shown in Table 2, the reactivity order, that is, the inhibitive effectiveness order, is PPBQ>PPQ. As a result, a satisfactory agreement has been found between the calculated and experimental data.
4 Conclusions
In summary, the extant experimental data and theoretical calculations presented in this study offer an in-depth inhibition efficiency comparison of the two quinoline chalcones in terms of their structural and electronic characteristics. There is a fair agreement between the electronic and global reactivity parameters of the protonated forms of PPQ and PPBQ and the experimental findings, which gives a considerable credence for the identified structures in acidic media. It has been confirmed that the most stable structures of PPQ and PPBQ in the aqueous phase are their protonated forms. The results of the DFT calculations indicate that the corrosion inhibition capabilities of these inhibitors decrease in the order PPBQ>PPQ, which also agrees well with the experimental findings.
References
Awad MK, Metwally MS, Soliman SA, El-Zomrawy AA, Bedair MA. Experimental and quantum chemical studies of the effect of poly ethylene glycol as corrosion inhibitors of aluminum surface. J Ind Eng Chem 2014; 20: 796–808.10.1016/j.jiec.2013.06.009Search in Google Scholar
Ayyannan G, Karthikeyan K, Vivekananthan SS, Gopiraman M, Rathinavelu A. Chemical and electrochemical investigations of high carbon steel corrosion inhibition in 10% HCl medium by quinoline chalcones. Ionics 2013; 19: 919–932.10.1007/s11581-012-0812-ySearch in Google Scholar
Berar U. Chalcones: compounds possessing a diversity in applications. Orbital Elec J Chem 2012; 4: 209–221.Search in Google Scholar
Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA Jr, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas Ö, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ. Gaussian 09 Revision C.01. Wallingford, CT: Gaussian, Inc., 2009.Search in Google Scholar
Fukui K. The role of frontier orbitals in chemical reactions. Angew Chem Int Ed 1982; 21: 801–809.10.1002/anie.198208013Search in Google Scholar
Gece G. The use of quantum chemical methods in corrosion inhibitor studies. Corros Sci 2008; 50: 2981–2992.10.1016/j.corsci.2008.08.043Search in Google Scholar
Gece G. Drugs: a review of promising novel corrosion inhibitors. Corros Sci 2011; 53: 3873–3898.10.1016/j.corsci.2011.08.006Search in Google Scholar
Gece G. Theoretical evaluation of the inhibition properties of two thiophene derivatives on corrosion of carbon steel in acidic media. Mater Corros 2013; 64: 940–944.10.1002/maco.201106482Search in Google Scholar
Gerengi H, Goksu H, Slepski P. The inhibition effect of mad honey on corrosion of 2007-type aluminium alloy in 3.5% NaCl solution. Mater Res 2014; 17: 255–264.10.1590/S1516-14392013005000174Search in Google Scholar
Khadom AA. Effect of corrosive solution motion on copper-nickel alloy pipe in presence of naphthylamine as a corrosion inhibitor. J Mater Environ Sci 2013; 4: 510–519.Search in Google Scholar
Koopmans T. Über die zuordnung von wellenfunktionen und eigenwerten zu den einzelnen elektronen eines atoms. Physica 1934; 1: 104–113.10.1016/S0031-8914(34)90011-2Search in Google Scholar
Lide DR. CRC Handbook of chemistry and physics. 85th ed., Boca Raton, FL: CRC Press, 2004.Search in Google Scholar
Lukovits I, Kalman E, Zucchi F. Corrosion inhibitors – correlation between electronic structure and efficiency. Corrosion 2001; 57: 3–8.10.5006/1.3290328Search in Google Scholar
Obot IB, Gasem ZM. Theoretical evaluation of corrosion inhibition performance of some pyrazine derivatives. Corros Sci 2014; 83: 359–366.10.1016/j.corsci.2014.03.008Search in Google Scholar
Obot IB, Macdonald DD, Gasem ZM. Density functional theory (DFT) as a powerful tool for designing new organic corrosion inhibitors. Part 1: an overview. Corros Sci 2015; doi: 10.1016/j.corsci.2015.01.037.10.1016/j.corsci.2015.01.037Search in Google Scholar
Palou RM, Xomelt OO, Likhanova NV. Environmentally friendly corrosion inhibitors. In: Aliofkhazraei M, editor. Developments in corrosion protection. Rijeka, Crotia: Intech, 2014: 1–36.Search in Google Scholar
Pauling L. The nature of the chemical bond. New York, NY: Cornell University Press, 1960.Search in Google Scholar
Pina F, Maestri M, Balzani V. Photochromic flavylium compounds as multistate/multifunction molecular-level systems. Chem Commun 1999; 2: 107–114.10.1039/a805522jSearch in Google Scholar
Pyykkö P, Atsumi M. Molecular double-bond covalent radii for elements Li-E112. Chem Eur J 2009; 15: 12770–12779.10.1002/chem.200901472Search in Google Scholar PubMed
Rabinovich D. Topochemistry. Part XXX. Crystal and molecular structures of chalcone. J Chem Soc B Phys Org 1970; 11.10.1039/j29700000011Search in Google Scholar
Tkalcec I. Mechanical properties and microstructure of a high carbon steel. PhD thesis, École Polytechnique Fédérale De Lausanne, 2004.Search in Google Scholar
Udhayakala P. Quantum chemical studies on the inhibition potentials of thiophene derivatives for the corrosion inhibitors of carbon steel. J Chem Pharm Res 2015; 7: 803–810.Search in Google Scholar
Xue Y, Liu Y, An L, Zhang L, Yuan Y, Mou J, Liu L, Zheng Y. Electronic structures and spectra of quinoline chalcones: DFT and TDDFT-PCM investigation. Comput Theor Chem 2011; 965: 146–153.10.1016/j.comptc.2011.01.042Search in Google Scholar
Yaylı N, Üçüncü O, Yaşar A, Gök Y, Küçük M, Kolaylı S. Stereoselective photochemistry of methoxy chalcones in solution and their radical scavenging activity. Turk J Chem 2004; 28: 515–521.Search in Google Scholar
Zarrouk A, El Ouali I, Bouachrine M, Hammouti B, Ramli Y, Essassi EM, Warad I, Aouniti A, Salghi R. Theoretical approach to the corrosion inhibition efficiency of some quinoxaline derivatives of steel in acid media using the DFT method. Res Chem Intermed 2013; 39: 1125–1133.10.1007/s11164-012-0671-1Search in Google Scholar
©2015 by De Gruyter
Articles in the same Issue
- Frontmatter
- In this issue
- Reviews
- Improvement of corrosion resistance of magnesium alloys for biomedical applications
- Environment-induced fatigue cracking behavior of aluminum alloys and modification methods
- On high-temperature oxidation and protection of 2:17-type SmCo-based magnets
- Corrosion behaviors of steels under supercritical CO2 conditions
- The natural gas industry: equipment, materials, and corrosion
- Original articles
- Modeling data acquisition during electrochemical noise measurements for corrosion studies
- Corrosion inhibition behavior of two quinoline chalcones: insights from density functional theory
Articles in the same Issue
- Frontmatter
- In this issue
- Reviews
- Improvement of corrosion resistance of magnesium alloys for biomedical applications
- Environment-induced fatigue cracking behavior of aluminum alloys and modification methods
- On high-temperature oxidation and protection of 2:17-type SmCo-based magnets
- Corrosion behaviors of steels under supercritical CO2 conditions
- The natural gas industry: equipment, materials, and corrosion
- Original articles
- Modeling data acquisition during electrochemical noise measurements for corrosion studies
- Corrosion inhibition behavior of two quinoline chalcones: insights from density functional theory

