Patent Clearinghouse and Technology Diffusion: What is the Contribution of Arbitration Agreements?

Appendix A: Non Profitability for U Not to License or Not to Produce in the Scenario Without PaC

Appendix B: Non Profitability for U Not to Produce in the Scenario with the PaC

Appendix C: Proposition 4

Direct comparison of the profits of firm U Firm in the possible scenarios reveals that U joins the PaC and offers

1. An exclusive contract (EC) for

   1. μ ∈ [0, 0.2920] ∩ η ∈ [(0.4048μ + 0.5952), 1],

   2. μ ∈ [0.2920, 0.4889] ∩ η ∈ [(1.4550μ + 0.2886), 1].

2. A non-exclusive contract (NC) for

   1. μ ∈ [0.2920, 0.3447] ∩ η ∈ [(0.0567μ + 0.6968), (1.4550μ + 0.2886)],

   2. μ ∈ [0.3447, 0.4889] ∩ η ∈ [(0.4327μ + 0.5672), (1.4550μ + 0.2886)],

   3. μ ∈ [0.4889, 1] ∩ η ∈ [(0.4327μ + 0.5672), 1].

Appendix D: Proof of Proposition 5

From the proof of Proposition 4 the minimum value of η for which Firm U joins the PaC is

Clearly, η ̲ is always larger than μ.

Appendix E: Effect of the IP Owner’s Membership in the PaC on the License Offer

Comparison Propositions 1 and 2 we conclude that:

1. In region μ ∈ [0.2920, 0.3447] ∩ η ∈ [(0.0567μ + 0.6968), (1.4550μ + 0.2886)], firm U’s membership in the PaC increases the number of license offered.

2. In region μ ∈ [0.3447, 0.4889] ∩ η ∈ [(1.4550μ + 0.2886), 1], firm U’s membership in the PaC restricts the license offered.

3. In all other regions firm U’s membership in the PaC does not affect the licenses offered.

Appendix F: Alternative Arbitration Pricing Schemes

We have carried out our analysis by assuming that the arbitrator implements non-linear contracts based on two-part tariffs. Our results remain qualitatively unchanged under two alternative, commonly used, payment schemes: a lump-sum transfer and a linear fee. Here we will limit ourselves to discuss how these pricing schemes affect the arbitration outcomes withing the clearinghouse.^[32]

Figure 3 depicts the two alternative tariff structures, and diagrammatically confirms our claim that the main message goes through with different arbitration pricing schemes. Two remarks are worth making, which will be helpful in the ensuing discussion. The first one is that – as in the main model – the IP owner always finds it profitable to produce its own good. The second one is that alternative pricing schemes affect only the outside options of the firms in the platform. This, in turn, entails that the equilibrium two-part tariffs governing the trade between firm U and firm 1 are modified only in the fixed fee, as the royalty rate remains the same as in the main text. The ultimate consequence is that the equilibrium prices, quantities and total surplus generated in the industry do not depend on the tariff structure implemented by the arbitrator, which affects only the equilibrium apportioning between U and 1 of the surplus generated by the sales of good 1.

Figure 3:

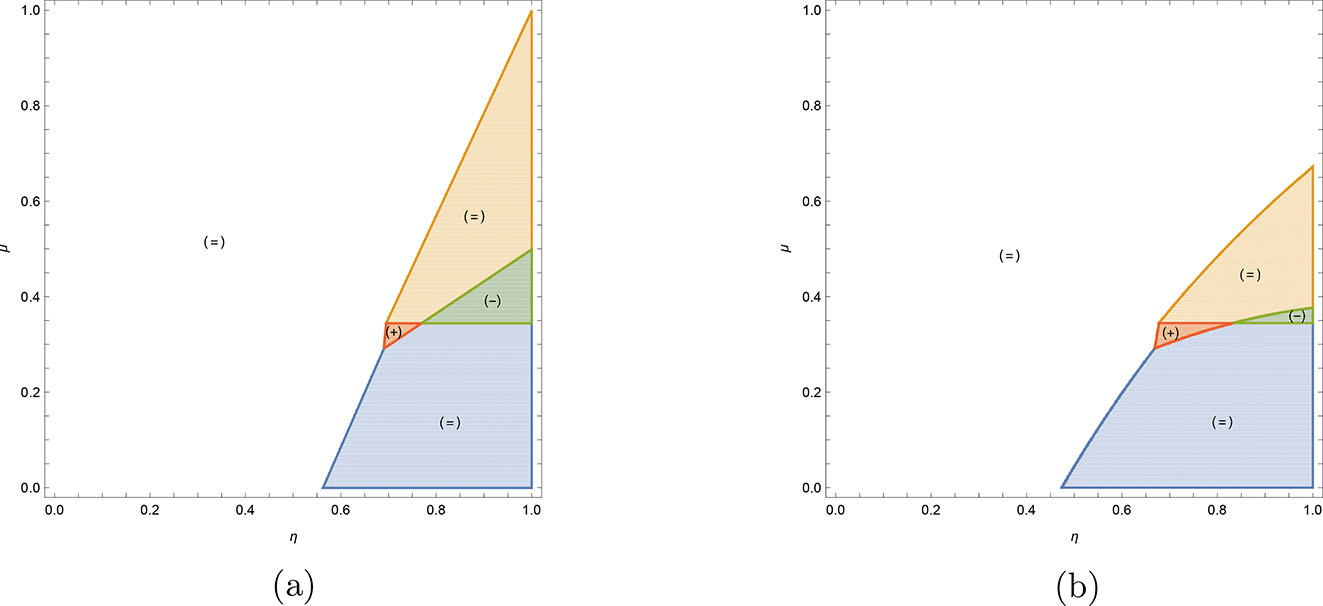
Alternative pricing schemes. (a) Lump-sum tariff. (b) Linear tariff.

The situation in which the arbitrator opts for a lump sum transfer mirrors the scenario discussed in the main text, with the royalty rate set to zero in case of disagreement. Because the arbitrator aims at maximizing the value of the license only, with a two-part tariff it sets a negative royalty rate, in order to boost the sales of good 1. As mentioned above, that negative royalty rate is too low from the standpoint of firm U. Consequently, the use by the arbitrator of a lump sum transfer, which implicitly amounts to increasing the royalty rate as compared to the two-part tariff, makes product 1 relatively less competitive than product U and increases the outside option of firm U at the expenses of that of firm 1. Eventually, this results in higher equilibrium profits for firm U than in the two-part tariff case. Yet, the ExE is still at work with a lump-sum tariff, because, the – implicit – royalty rate under a lump sum transfer, although larger than that under the arbitrated two-part tariff, still falls short of the one maximizing the joint profit of firms U and 1. Therefore, for given η and μ, U finds it more attractive to join the PaC with the arbitration tariff being a fixed fee.

With linear tariffs, the royalty rate both determines the total surplus to be shared and the apportioning thereof, thus the efficiency of linear tariffs within the vertical hierarchy is lower than that of non-linear contracts. It is clear that firm 1 would select the lowest rate acceptable to firm U, namely zero, while firm U would choose the one maximizing its own profit: label this royalty rate w ^U  > 0.^[33] Clearly the arbitrator must choose a value between these two extremes, and accordingly, we assume that the chosen royalty rate is a weighted average of these extremes, with weights equal to the preference of the arbitrator for the firms, namely η × w ^U  + (1 − η) × 0. An immediate consequence is that, for any η < 1 the arbitrated royalty rate is lower than the one which fully internalizes the effect on the profits of firm U, which results in the existence of the ExE. Interestingly, in this case the actual size of this effect is negatively correlated with η. Consequently, the attractiveness of joining the PaC for firm U is larger under linear contracts than under two-part tariffs only if η is large enough.