Abstract
The public provision of long-term care (LTC) can replace family-provided LTC when adults are not sufficiently altruistic towards their parents. But State intervention can modify the transmission of values and reduce the long-run prevalence of family altruism. To characterize the optimal LTC policy, we develop a three-period OLG model where the adult population is divided into altruistic and non-altruistic agents, and where the transmission of altruism follows a socialization process `a la Bisin and Verdier (2001, The economics of cultural transmission and the dynamics of preferences. Journal of Economic Theory 97:298–319). It is shown that public LTC benefits, by reducing parental investment in children, make the long-run survival of family altruism less likely. However, whether crowding out arises or not depends on individual preferences and on the socialization mechanism at work. We also study the incompatibility of the optimal short-run LTC benefits with long-run social welfare maximization. Finally, we discuss the robustness of our results to introducing savings and universal LTC benefits.
Appendix
Proof of Proposition 2
The dynamics of the economy is described by the equation:
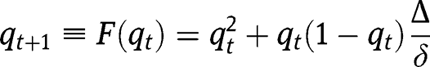
The existence, uniqueness and stability of a stationary equilibrium can be studied by analyzing the properties of the transition function 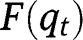 .
.
Note that 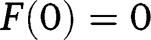 and
and 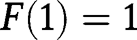 , so that both
, so that both 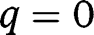 and
and 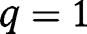 , being fixed points of
, being fixed points of  , are stationary equilibria. Regarding the existence of an intermediate equilibrium, note that:
, are stationary equilibria. Regarding the existence of an intermediate equilibrium, note that: 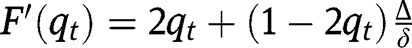 . Given the interiority of effort level (i.e.
. Given the interiority of effort level (i.e. 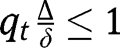 and
and 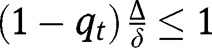 ), the derivative is always positive, so that
), the derivative is always positive, so that  is increasing. We also have:
is increasing. We also have: 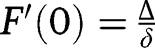 and
and 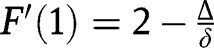 . Hence, if
. Hence, if 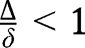 , we have:
, we have: 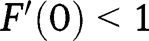 and
and 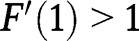 , so that
, so that 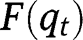 lies below the 45° line in the neighbourhood of 0, and below the 45° line in the neighbourhood of 1. We have also:
lies below the 45° line in the neighbourhood of 0, and below the 45° line in the neighbourhood of 1. We have also: 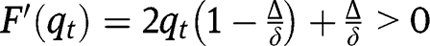 and
and 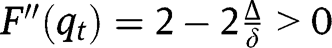 . Given
. Given 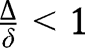 , we have
, we have 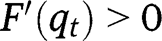 and
and 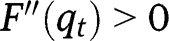 for all levels of
for all levels of 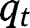 , so that
, so that 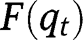 is increasing and convex, and admits no inflection point, and remains below the 45° line for
is increasing and convex, and admits no inflection point, and remains below the 45° line for 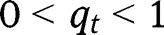 . Hence, in that case, there is no intermediate stationary equilibrium. Moreover, only
. Hence, in that case, there is no intermediate stationary equilibrium. Moreover, only 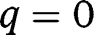 is locally stable, as:
is locally stable, as: 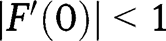 and
and 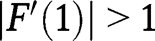 . Alternatively, if
. Alternatively, if 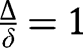 , we have
, we have 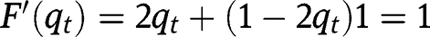 .
. 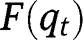 is linear and of slope 1. Hence, given
is linear and of slope 1. Hence, given 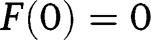 , this coincides with the 45° line, so that any partition of the population is a stationary partition. There is a continuum of stationary equilibria, all of these being unstable.
, this coincides with the 45° line, so that any partition of the population is a stationary partition. There is a continuum of stationary equilibria, all of these being unstable.
Finally, if 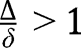 , we have
, we have 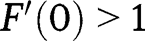 and
and 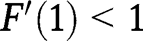 , so that the transition function lies above the 45° line in the neighbourhood of 0, and above the 45° line in the neighbourhood of 1. Taking the second-order derivative, we have:
, so that the transition function lies above the 45° line in the neighbourhood of 0, and above the 45° line in the neighbourhood of 1. Taking the second-order derivative, we have: 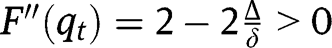 . Given
. Given 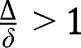 , we have
, we have 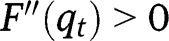 for all levels of
for all levels of 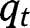 , so that
, so that 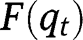 is concave. There cannot be an intermediate equilibrium, since it would imply:
is concave. There cannot be an intermediate equilibrium, since it would imply: 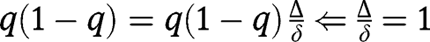 , which is incompatible with
, which is incompatible with 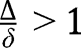 . Hence, there is no intermediate stationary equilibrium, and only
. Hence, there is no intermediate stationary equilibrium, and only 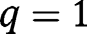 is locally stable, as
is locally stable, as 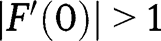 and
and 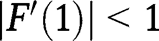 .
.
Proof of Proposition 3
Consider now the “It takes a village” technology. We have:
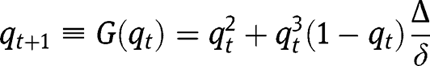
We have: 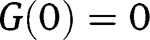 ,
, 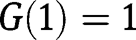 . Hence both
. Hence both 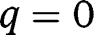 and
and 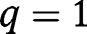 , being fixed points of
, being fixed points of 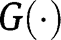 , are stationary equilibria. Regarding the existence of an intermediate equilibrium, note that:
, are stationary equilibria. Regarding the existence of an intermediate equilibrium, note that: 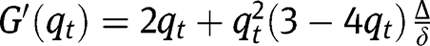 . Here again, interiority conditions for effort imply that
. Here again, interiority conditions for effort imply that 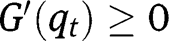 . For extreme
. For extreme 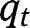 , we have
, we have 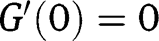 and
and 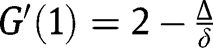 . Hence
. Hence 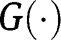 lies below the 45° line in the neighbourhood of 0 and lies above or below the 45° line in the neighbourhood of 1, depending on
lies below the 45° line in the neighbourhood of 0 and lies above or below the 45° line in the neighbourhood of 1, depending on  . Thus, if
. Thus, if 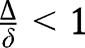 ,
, 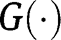 lies below the 45° line in the neighbourhood of 1. On the contrary, if
lies below the 45° line in the neighbourhood of 1. On the contrary, if 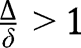 , then
, then 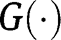 lies above the 45° line in the neighbourhood of 1. As a consequence, there must exist at least one intersection of
lies above the 45° line in the neighbourhood of 1. As a consequence, there must exist at least one intersection of 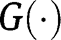 with the 45° line for a level of
with the 45° line for a level of 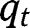 that is larger than 0 and smaller than 1: an intermediate steady-state must then exist. Note also that the second-order derivative is
that is larger than 0 and smaller than 1: an intermediate steady-state must then exist. Note also that the second-order derivative is 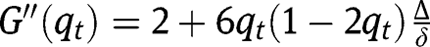 . Its sign is ambiguous and may depend on
. Its sign is ambiguous and may depend on 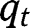 . Note that:
. Note that: 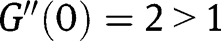 and
and 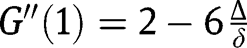 . Thus, the transition function is convex around
. Thus, the transition function is convex around 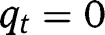 and may turn out to be concave at
and may turn out to be concave at 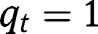 , provided
, provided 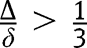 .
.
To study the stability of the stationary equilibria, note that 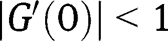 . Hence
. Hence 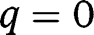 is a locally stable equilibrium. Moreover, we have, when
is a locally stable equilibrium. Moreover, we have, when 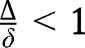 :
: 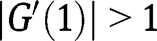 , so that
, so that 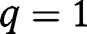 is not stable in that case. However, when
is not stable in that case. However, when 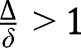 , we have
, we have 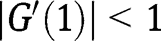 , so that
, so that 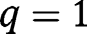 is then locally stable.
is then locally stable.
Regarding the intermediate stationary equilibrium, note that equalizing 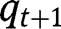 and
and 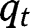 in the transition function yields:
in the transition function yields: 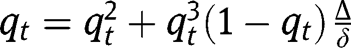 . From which we get a unique value:
. From which we get a unique value: 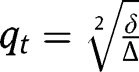 . Thus the interior equilibrium is unique when
. Thus the interior equilibrium is unique when 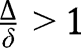 and does not exist when
and does not exist when 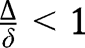 . To study its stability, let us notice that:
. To study its stability, let us notice that: 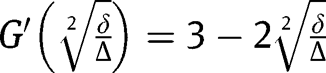 . Given that
. Given that 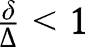 , we necessarily have
, we necessarily have 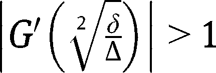 , implying instability. Finally, note that, if
, implying instability. Finally, note that, if 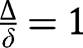 , there exist only two stationary equilibria,
, there exist only two stationary equilibria, 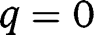 and
and 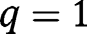 . Moreover, we have
. Moreover, we have 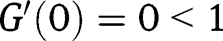 and
and 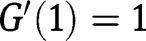 . Hence only
. Hence only 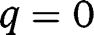 is locally stable.
is locally stable.
Proof of Proposition 5
The dynamics of the economy is described by the equation:
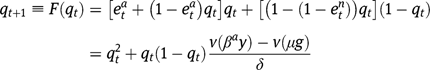
The existence, uniqueness and stability of a stationary equilibrium can still be studied by analyzing the properties of 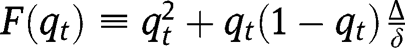 , where
, where 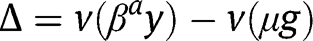 instead of
instead of 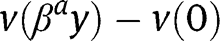 at the laissez-faire. The existence and stability analyses, which are close to the ones under the laissez-faire, are not reproduced here.
at the laissez-faire. The existence and stability analyses, which are close to the ones under the laissez-faire, are not reproduced here.
Proof of Proposition 6
The dynamics of the economy is described by the equation:
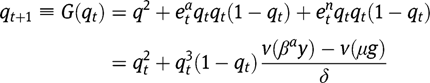
The existence, uniqueness and stability of a stationary equilibrium can thus be studied by analyzing the properties of 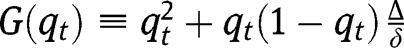 , where
, where 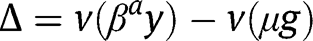 instead of
instead of 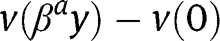 at the laissez-faire. Those analyses being close to the ones under the laissez-faire ones are not reproduced here.
at the laissez-faire. Those analyses being close to the ones under the laissez-faire ones are not reproduced here.
Proof of Proposition 9
If 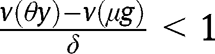 for any
for any 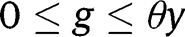 , we have, in the long-run,
, we have, in the long-run, 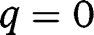 . That result holds whatever g is. Hence, in that case where public intervention has no effect on the population dynamics, the optimal policy in the long-run consists of the optimal policy in the short-run, that is, a LTC benefit
. That result holds whatever g is. Hence, in that case where public intervention has no effect on the population dynamics, the optimal policy in the long-run consists of the optimal policy in the short-run, that is, a LTC benefit 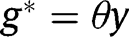 from non-altruistic children towards their parents.
from non-altruistic children towards their parents.
If 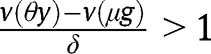 for any
for any 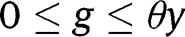 , the long-run composition of the population is
, the long-run composition of the population is 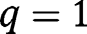 . That result holds whatever g is. Hence, in that case, the optimal long-run policy is the laissez-faire. However, in the short-run, it is optimal to implement a LTC benefit
. That result holds whatever g is. Hence, in that case, the optimal long-run policy is the laissez-faire. However, in the short-run, it is optimal to implement a LTC benefit 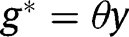 from non-altruistic children towards their parents.
from non-altruistic children towards their parents.
Otherwise, if we exclude those two cases, the level of g will determine the long-run composition of the population. In other words, there exists a threshold 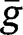 such that
such that 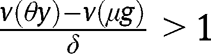 for any
for any 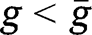 and
and 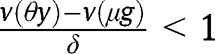 for any
for any 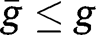 . The convergence towards the stationary equilibrium with
. The convergence towards the stationary equilibrium with 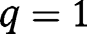 requires:
requires: 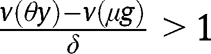 . Hence, it is necessary that
. Hence, it is necessary that 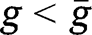 . This implies that the LTC benefit should be lower than the optimal short-run benefit
. This implies that the LTC benefit should be lower than the optimal short-run benefit 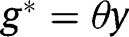 .
.
Proof of Proposition 10
Consider first the case where 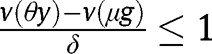 for any
for any 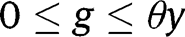 . In that case, the long-run composition of the population is
. In that case, the long-run composition of the population is 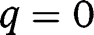 . That result holds whatever the level of g is. Hence, in that case where the public intervention has no effect on the population dynamics, the optimal policy in the long-run consists of the optimal policy in the short-run, that is, a LTC benefit
. That result holds whatever the level of g is. Hence, in that case where the public intervention has no effect on the population dynamics, the optimal policy in the long-run consists of the optimal policy in the short-run, that is, a LTC benefit 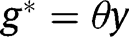 from non-altruistic children towards their parents.
from non-altruistic children towards their parents.
If 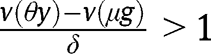 for any
for any 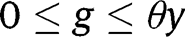 , the long-run composition of the population is
, the long-run composition of the population is 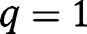 . Here again, that result holds whatever the LTC benefit g is. In that case, the public intervention has no effect on the population dynamics and thus the policy is not constrained by evolutionary forces.
. Here again, that result holds whatever the LTC benefit g is. In that case, the public intervention has no effect on the population dynamics and thus the policy is not constrained by evolutionary forces.
Otherwise, if we exclude those two cases, the level of g will determine the long-run composition of the population. In other words, there exists a threshold 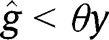 such that
such that 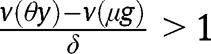 and if
and if 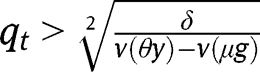 for any
for any 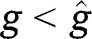 and
and 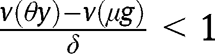 and/or
and/or 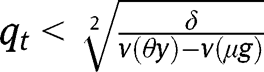 for any
for any 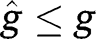 . The convergence towards the stationary equilibrium with
. The convergence towards the stationary equilibrium with 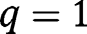 requires:
requires: 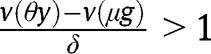 . implying
. implying 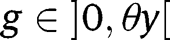 . Moreover, unlike in the “It’s the family” case, we need also
. Moreover, unlike in the “It’s the family” case, we need also 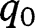 to be strictly larger than the intermediate equilibrium, implying
to be strictly larger than the intermediate equilibrium, implying 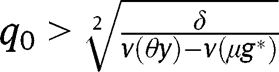 .
.
Proof of Proposition 12
The proof of Proposition 12 is very close to the proof of Proposition 2, except that  is here linear. When
is here linear. When 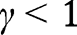 , we have
, we have 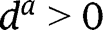 , and the analysis is carried out as in the proof of Proposition 2. Here again, three cases can arise, depending on
, and the analysis is carried out as in the proof of Proposition 2. Here again, three cases can arise, depending on 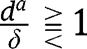 . If
. If 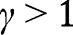 , all efforts are zero. There are two equilibria,
, all efforts are zero. There are two equilibria, 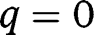 (locally stable) and
(locally stable) and 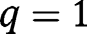 (unstable).
(unstable).
Proof of Proposition 13
The proof of Proposition 13 is very close to the proof of Proposition 5, except that  is here linear. When
is here linear. When 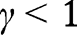 , we have
, we have 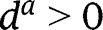 , and the analysis is carried out as in the proof of Proposition 5. Here again, three cases can arise, depending on
, and the analysis is carried out as in the proof of Proposition 5. Here again, three cases can arise, depending on 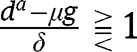 . If
. If 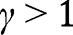 , all efforts are zero. There are two equilibria,
, all efforts are zero. There are two equilibria, 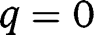 (locally stable) and
(locally stable) and 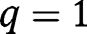 (unstable).
(unstable).
Proof of Proposition 14
Under 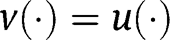 , we obtain, in the case of targeted LTC benefits:
, we obtain, in the case of targeted LTC benefits:
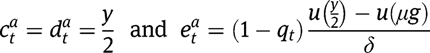
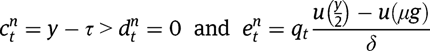
while, in the case of universal benefits:
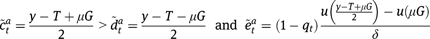
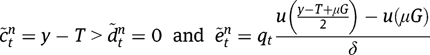
Since 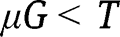 ,
, 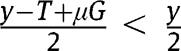 , so that, under equal-sized policies (i.e.
, so that, under equal-sized policies (i.e. 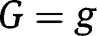 ), we obtain:
), we obtain: 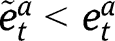 and
and 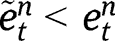 .
.
Proof of Proposition 15
The proof is similar to the proof of Proposition 5, except for the definition of the conditions, which is based now on the socialization effort levels studied in Section 6.2. Therefore those analyses are not reproduced here.
Proof of Proposition 16
The proof is similar to the proof of Proposition 8, except for the definition of the conditions, which is based now on the socialization effort levels studied in Section 6.2. Therefore those analyses are not reproduced here.
Acknowledgements
I am grateful to Chiara Canta, Arnold Chassagnon, Helmuth Cremer, Edward Norton, Sergio Perelman, Pierre Pestieau, Manuel Plisson, Luigi Siciliani, Steven Stern, Emmanuel Thibault and two anonymous referees for their helpful comments on this article.
References
Bisin, A., and T.Verdier. 2001. “The Economics of Cultural Transmission and the Dynamics of Preferences.” Journal of Economic Theory97:298–319.10.1006/jeth.2000.2678Search in Google Scholar
Bisin, A., and T.Verdier. 2010. “The Economics of Cultural Transmission and Socialization.” NBER WP 16512.10.3386/w16512Search in Google Scholar
Brown, J., and A.Finkelstein. 2004a. “Supply or Demand: Why Is the Market for LTC Insurance So Small?” NBER WP 10782.10.3386/w10782Search in Google Scholar
Brown, J., and A.Finkelstein. 2004b. “The Interaction of Public and Private Insurance: Medicaid and the LTC Insurance Market.” NBER WP 10989.10.3386/w10989Search in Google Scholar
Canta, C., and P.Pestieau. 2012. “LTC Insurance and Family Norms.” mimeo.Search in Google Scholar
Cremer, H., F.Gahvari, and P.Pestieau. 2012. “Uncertain Altruism and Long Term Care.” mimeo.Search in Google Scholar
Cutler, D.1993. “Why Doesn’t the Market Fully Insure Long Term Care?” NBER WP 4301.10.3386/w4301Search in Google Scholar
De Donder, P., and P.Pestieau. 2011. “Private, Social and Self-Insurance for Long-Term Care: A Political Economy Analysis.” CORE Discussion Paper 2011-53.Search in Google Scholar
European Union.2009. “The 2009 Ageing Report.” Joint Report prepared by the European Commission (DGECFIN) and the Economic Policy Committee (AWG).Search in Google Scholar
Finkelstein, A., and K.McGarry. 2003. “Private Information and Its Effect on Market Equilibrium: New Evidence from LTC Market.” NBER WP 9957.10.3386/w9957Search in Google Scholar
Hammond, P.1987. “Altruism.” In The New Palgrave: A Dictionary of Economics, edited by J.Eatwell, M.Milgate, and P.Newman, 85–86. London: Macmillan.10.1057/978-1-349-95121-5_470-1Search in Google Scholar
Hoerger, T. J., G.Picone, and F.Sloan. 1996. “Public Subsidies, Private Provision of Care and Living Arrangements.” Review of Economics and Statistics78(3):428–40.10.2307/2109790Search in Google Scholar
Jousten, A., B.Lipszyc, M.Marchand, and P.Pestieau. 2005. “Long Term Care Insurance and Optimal Taxation for Altruistic Children.” FinanzArchiv61:1–18.10.1628/0015221053722514Search in Google Scholar
Kemper, P., and C. M.Murtaugh. 1991. “Lifetime Use of Nursing Home Care.” New England Journal of Medicine324:595–600.10.1056/NEJM199102283240905Search in Google Scholar
Norton, E.2000. “Long Term Care.” In Handbook of Health Economics, edited by A.Cuyler and J.Newhouse, vol. 1, chap. 17. Amsterdam: North-Holland.Search in Google Scholar
OECD.2006. “Projecting OECD Health Care and Long-Term Care Expenditures.” OECD Economics Department Working Paper 477.Search in Google Scholar
Olivera, J.2011. “Old Age Support and Demographic Change in Developing Countries.” A cultural transmission model, Working Paper, Department of Economics, Catholic University of Leuven.Search in Google Scholar
Pestieau, P., and G.Ponthiere. 2011. “Long Term Care Insurance Puzzle.” In Financing Long Term Care in Europe: Institutions, Markets and Models, edited by J.Costa-Font and C.Courbage, 41–52. London: Palgrave Macmillan.10.1057/9780230349193_3Search in Google Scholar
Pestieau, P., and M.Sato. 2008. “Long Term Care: The State, the Market and the Family.” Economica75:435–54.10.1111/j.1468-0335.2007.00615.xSearch in Google Scholar
Ponthiere, G.2010. “Unequal Longevities and Lifestyles Transmission.” Journal of Public Economic Theory12(1):93–126.10.1111/j.1467-9779.2009.01449.xSearch in Google Scholar
Ponthiere, G.2011. “Mortality, Family and Lifestyles.” Journal of Family and Economic Issues32(2):175–90.10.1007/s10834-010-9229-9Search in Google Scholar
Sloan, F., and E.Norton. 1997. “Adverse Selection, Bequests, Crowding Out, and Private Demand for Insurance: Evidence From the LTC Insurance Market.” Journal of Risk and Uncertainty15:201–19.10.1023/A:1007749008635Search in Google Scholar
Sloan, F., G.Picone, and T.Hoeger. 1997. “The Supply of Children’s Time to Disabled Elderly Parents.” Economic Inquiry35:295–308.10.1111/j.1465-7295.1997.tb01911.xSearch in Google Scholar
Taleyson, L.2003. “L’Assurance Dépendance Privée: Comparaisons Internationales.” Newsletters Techniques SCOR.Search in Google Scholar
- 1
For instance, the average cost of institutional LTC for old persons in France is about 35,000 euros per year (OECD 2006), while the yearly price of a nursing home in the United States ranges between $40,000 and $75,000 (see Taleyson 2003).
- 2
See Pestieau and Ponthiere (2011) for a survey.
- 3
On old-age dependency risks, see Kemper and Murtaugh (1991).
- 4
Large loading factors for LTC insurance may be caused by adverse selection.
- 5
Our article differs from Canta and Pestieau (2012), who focus on a dynamic economy composed of traditional and opportunistic agents under exogenous transition probabilities.
- 6
In that framework, individuals can neither save resources for their old days nor purchase private LTC insurance. The reason why we make those assumptions lies in individual misperception of LTC risks in the real world (Finkelstein and McGarry 2003) and in the underdevelopment of private LTC insurance markets. Those facts motivate us to develop a baseline model that focuses on a provision of LTC either by the family or by the State. The possibility of self-insurance through private savings is discussed in Section 6.1 below.
- 7
We assume here no risk about the length of life, which is a significant simplification. See Ponthiere (2010) on the interactions of life expectancy with the socialization process.
- 8
The implications of introducing savings are discussed in Section 6.1.
- 9
For simplicity, we abstract here from family altruism oriented towards children.
- 10
Assuming a single input in the production of old-age welfare leads us to abstract here from the choice between formal and informal aid. However, given that our focus is on crowding out by the State that simplification is benign.
- 11
Fixing
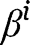 to either 0 or 1 is an obvious simplification, but which has only minor effects on our results. We will discuss later on the influence of that assumption on our findings.
to either 0 or 1 is an obvious simplification, but which has only minor effects on our results. We will discuss later on the influence of that assumption on our findings. - 12
Assuming a physical effort – rather than an effort in terms of time or goods – is a simplification, which is common to the literature on cultural transmission (see Bisin and Verdier 2010). That assumption ensures that there are no income effects on socialization (see infra).
- 13
For simplicity, we assume here that socialization costs are symmetric across types. As discussed in Ponthiere (2011), introducing asymmetric socialization costs can affect long-run population dynamics. However, in our context where all parents want to transmit the same trait, it is not obvious to see why some type of parents would face smaller socialization costs.
- 14
As such, we depart from Olivera (2011).
- 15
Such efforts are widespread in real life and often take the form of family stories or justifications, which are used by parents to convince their children not to behave like them. Adults who abandon their parents can try to justify that attitude by giving to their own children some reasons why they are right to do so in their particular case, even though abandoning elderly parents is not good in general.
- 16
The probability of direct vertical socialization depends here on the true proportion of young adults who help their elderly parents and not on some beliefs about that proportion. That assumption has important consequences. Clearly, if beliefs affected socialization efforts, then the overall dynamics might be modified, with a larger occurrence of multiple equilibria. Moreover, relaxing the perfect observability assumption could affect the design of the optimal policy. Section 6.2, which considers universal LTC benefits, partly relaxes the perfect observability assumption, by assuming that the government cannot identify elderly persons with non-altruistic children (see infra).
- 17
On demonstration effects, see Canta and Pestieau (2012).
- 18
See Section 7 for a discussion on various possible extensions.
- 19
As
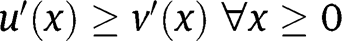 , the share
, the share 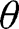 lies between 0 and
lies between 0 and 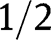 .
. - 20
Throughout this article, we assume the interiority of optimal socialization efforts, with
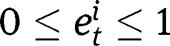 . This imposes some (weak) restrictions on
. This imposes some (weak) restrictions on  and on the parameter
and on the parameter 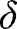 . For instance, in the case of “It’s the family”, interiority conditions are
. For instance, in the case of “It’s the family”, interiority conditions are 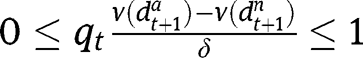 and
and 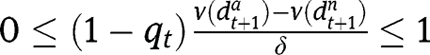 .
. - 21
Otherwise, it is better not to socialize children and to let them take their egoistic trait in a costless way.
- 22
Hence, interiority conditions for
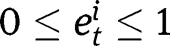 are
are 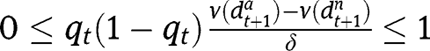 and
and 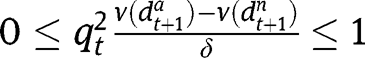 .
. - 23
We do not consider here whether such a LTC policy would emerge from voting. But there are strong reasons to believe that it would: parents of non-altruistic children are in favour, as well as young altruistic children (since it would reduce their socialization efforts). Parents of altruistic children are indifferent, and only non-altruistic children are likely to be against. Hence, assuming that
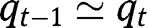 , the proposal of a LTC policy would obtain the majority of votes. On voting on LTC in a more general environment with unequal wages and dependence risk, see De Donder and Pestieau (2011).
, the proposal of a LTC policy would obtain the majority of votes. On voting on LTC in a more general environment with unequal wages and dependence risk, see De Donder and Pestieau (2011). - 24
In the rest of this article, we focus on the case where
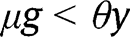 , to rule out corner solutions. That restriction is not problematic since the optimal policy always satisfies that condition.
, to rule out corner solutions. That restriction is not problematic since the optimal policy always satisfies that condition. - 25
Note that the interior conditions for
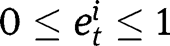 are necessarily weaker here than at the laissez-faire. Hence we will not pay too much attention to these in this section.
are necessarily weaker here than at the laissez-faire. Hence we will not pay too much attention to these in this section. - 26
Note, however, that the reliance on non-monetary efforts limits the influence of LTC benefits on socialization, since our framework abstracts from possible income effects.
- 27
This “crowding-out” effect differs from the usual one, where public intervention only affects the behaviour of some agent of a particular type. Here, LTC benefits affect the economy by modifying socialization efforts, and hence, the partition of the population into different types. Thus the “crowding-out” effect consists here of more than changing individual behaviours: it changes (some) individuals’ type, and, as a corollary, their behaviours as well.
- 28
Note also that, if we had
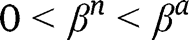 instead of
instead of 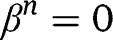 , what would matter for the existence of crowding out would no longer be the slope of
, what would matter for the existence of crowding out would no longer be the slope of  at 0, but, rather, the slope of
at 0, but, rather, the slope of  at the (strictly positive) level of help given by type-n children.
at the (strictly positive) level of help given by type-n children. - 29
That social objective is formally similar to the one studied in Jousten et al. (2005).
- 30
Given that the partition of the population is assumed to be fixed, we will leave aside the choice of socialization efforts
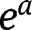 and
and 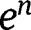 , which are set to 0.
, which are set to 0. - 31
Note that, by focusing on the best stationary equilibrium, we deliberately abstract from the transition towards the steady-state.
- 32
Given that the partition of the population is assumed to be fixed, we will leave aside the choice of socialization efforts
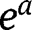 and
and 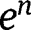 , which are set to 0.
, which are set to 0. - 33
As a consequence, the variables
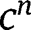 and g become irrelevant.
and g become irrelevant. - 34
The influence of intergenerational composition effects on optimal policy in the context of socialization models was also highlighted in Ponthiere (2010), but in the context of choices affecting one’s welfare rather than the welfare of others.
- 35
We assume here, for simplicity, that the interest factor R equals 1.
- 36
Those strategic interactions are studied in Cremer, Gahvari, and Pestieau (2012).
- 37
Note that this assumption departs from the assumption
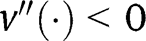 made in Section 2, since
made in Section 2, since 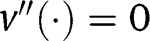 under quasi-linear preferences.
under quasi-linear preferences. - 38
For each agent, the optimal consumptions, aid and savings are independent from time. This is why we get rid of time indexes. We also ignore the case where
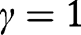 , since there is then, for type a, perfect indifference between aid and savings, making
, since there is then, for type a, perfect indifference between aid and savings, making 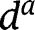 indeterminate.
indeterminate. - 39
Indeed, under quasi-linear utility, public LTC benefits towards the elderly in need cannot be justified from the point of view of maximizing social welfare for a given q.
- 40
Indeed, as long as savings is not as good as children’s aid, even if a government could force the elderly to save, such a solution may still be dominated by a fully altruistic society.
- 41
Note that the argument made here also holds in the “It takes a village” case.
- 42
Indeed, whereas targeted LTC benefits reduced the welfare gap between having altruistic children or not, universal LTC benefits still reduces the gap (given the concavity of
 ), but less than the targeted ones, which pushes towards more socialization.
), but less than the targeted ones, which pushes towards more socialization. - 43
Here again, we abstract from time indexes.
©2014 by Walter de Gruyter Berlin / Boston
Articles in the same Issue
- Frontmatter
- Editorial
- The Economics of Long-Term Care: An Introduction
- Advances
- The Economics of Long-Term Care
- Informal Care and Inter-vivos Transfers: Results from the National Longitudinal Survey of Mature Women
- Long-Term Care Insurance and Family Norms
- Long-Term Care, Altruism and Socialization
- Working Mums and Informal Care Givers: The Anticipation Effect
- Endogenous Altruism, Redistribution, and Long-Term Care
- Do Local Governments Respond to (Perverse) Financial Incentives in Long-Term Care Funding Schemes?
- Behavioral Biases and Long-Term Care Insurance: A Political Economy Approach
- Physical Activity and Policy Recommendations: A Social Multiplier Approach
Articles in the same Issue
- Frontmatter
- Editorial
- The Economics of Long-Term Care: An Introduction
- Advances
- The Economics of Long-Term Care
- Informal Care and Inter-vivos Transfers: Results from the National Longitudinal Survey of Mature Women
- Long-Term Care Insurance and Family Norms
- Long-Term Care, Altruism and Socialization
- Working Mums and Informal Care Givers: The Anticipation Effect
- Endogenous Altruism, Redistribution, and Long-Term Care
- Do Local Governments Respond to (Perverse) Financial Incentives in Long-Term Care Funding Schemes?
- Behavioral Biases and Long-Term Care Insurance: A Political Economy Approach
- Physical Activity and Policy Recommendations: A Social Multiplier Approach

