The quantum revolution in enzymatic chemistry: combining quantum and classical mechanics to understand biochemical processes

The foundation of modern computational enzymology

The 2013 Nobel Prize in Chemistry marked a milestone for computational biochemistry, signalling the maturity achieved by methods developed during previous decades and their application to the study of enzymatic catalysis. The Royal Swedish Academy of Sciences awarded the prize to three theoretical chemists – Martin Karplus, Michael Levitt and Arieh Warshel – “for the development of multiscale models for complex chemical systems”. This recognition highlighted the transformative impact of their work, particularly in combining quantum mechanics (QM) and molecular mechanics (MM) to simulate biomolecular processes, addressing the fundamental challenge of balancing computational accuracy with efficiency when modelling large systems. ¹

At its core, the QM/MM approach divides the enzymatic system into at least two regions: a quantum mechanical (QM) region encompassing the active site where chemical transformations occur, and a molecular mechanical (MM) region comprising the remainder of the protein and solvent environment (see Fig. 1). The QM region is treated using methods that can describe electronic structure, allowing for the modelling of bond breaking and formation, charge transfer, and polarization effects. Meanwhile, the MM region is represented using classical force fields that efficiently capture structural and environmental effects through simplified potential energy functions. The idea of applying different computational methods to different parts of the same molecular system was first put into practice with the calculation of the spectra of organic molecules with π-electrons. ² The first application of QM/MM methods to the study of enzymatic reactivity was the study of carbonium ion formation in the active site of lysozyme. ³ This seminal contribution already introduced a key idea for understanding enzymatic catalysis that has remained basically unchanged to this day: “It is found that electrostatic stabilization is an important factor in increasing the rate of the reaction step that leads to the formation of the carbonium ion intermediate.”

Fig. 1:

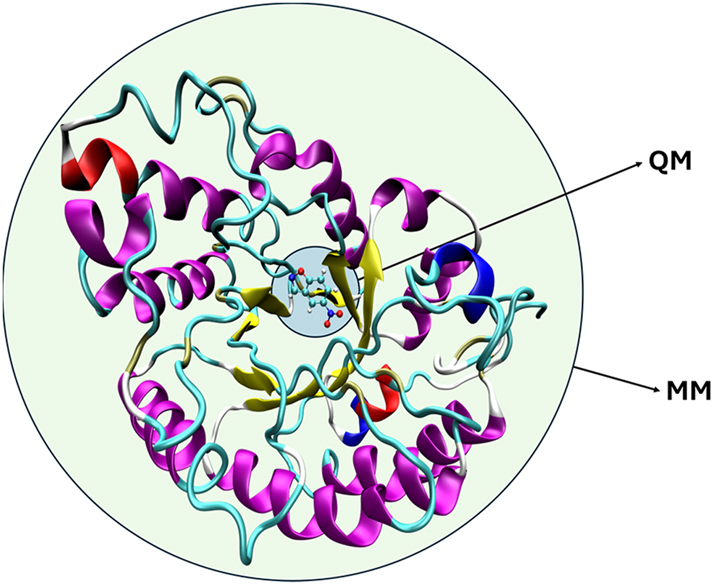
Schematic representation of the division of enzyme-substrate complex into a QM and a MM subsystems.

The fundamental insight that made QM/MM revolutionary was its ability to overcome the restrictions inherent to quantum mechanical calculations when applied to very large systems. QM/MM methods enabled researchers to use quantum mechanical calculations to study reactions taking place in enzymatic active sites, representing the surrounding protein environment with computationally efficient yet realistic molecular mechanics descriptions. In the decades following the pioneering work of Karplus, Levitt, and Warshel, QM/MM methods have evolved considerably, both regarding methodology and applications. ^{4 , 5 , 6 , 7} The original concepts have been refined with improved boundary treatments, more sophisticated quantum mechanical methods, and enhanced sampling techniques. Computational power advancements have enabled increasingly accurate calculations on larger systems, expanding the scope and impact of QM/MM studies in enzymology and drug design. ^{8 , 9} QM/MM approaches have become essential tools for understanding how enzymes achieve their remarkable catalytic efficiencies, providing insights that would be inaccessible through experimental methods alone. This theoretical framework has transformed our conceptual understanding of enzyme function from the simplified lock-and-key model to a detailed electronic description of enzymatic catalysis. The foundational principles established by Karplus, Levitt, and Warshel created a methodological bridge between the quantum world and biological macromolecules, enabling researchers to explore the fundamental physical processes underlying enzymatic catalysis.

The 2013 Nobel Prize in Chemistry celebrated the groundwork for computational enzymology by enabling atomic-level simulations of enzymatic reactions, while the 2024 Nobel Prize in Chemistry represents its logical culmination, a conceptual leap from understanding to design. The 2024 laureates – David Baker, Demis Hassabis, and John Jumper – developed computational tools to design sequences and structures of enzymes. ^{10 , 11} This progression closes the loop between computational analysis and synthetic biology, with QM/MM acting as a critical connection. By elucidating reaction mechanisms, QM/MM simulations generated fundamental principles, such as transition-state stabilization and electrostatic preorganization, nowadays employed to engineer functional active sites. Together, these tools have transformed enzymatic catalysis from a natural phenomenon to be dissected into a technology to be engineered. The 2013 and 2024 Nobels thus bookend a revolution: QM/MM illuminated how enzymes work, while modern design tools now answer how to build them.

This contribution reflects our personal experience in the use of quantum chemistry methods to analyze, replicate and predict enzyme catalysis. We briefly discuss the main methodological options, the theoretical framework needed to apply these methods to enzymatic catalysis and the main lessons learned about enzymatic catalysis during the last decades. We also discuss some of the possible directions for the field in the near future. The celebration of the International Year of Quantum Science and Technology is an excellent opportunity to recall what quantum chemistry has contributed and will contribute not only to understand nature, but also to improve the life of human beings, assisting in the development of new weapons to fight diseases or of new catalysts for the chemical industry.

Quantum methods in enzymatic reactivity and their connection to rate theory

The computational analysis of chemical reactivity is necessarily based on the use of quantum chemistry tools. A correct description of the changes in the electronic structure of the reacting molecules is required to quantify the energy changes taking place during the evolution of the nuclei from a rearrangement corresponding to reactants to one corresponding to products. This can be routinely performed for small systems if the surroundings can be ignored, as in gas phase reactions, or if it can be simplified to a passive unreactive environment, as in continuum model treatments. However, the situation is completely different in the case of enzymes. In this case the electronic changes associated with the chemical reaction take place in a complex and flexible environment that influences the energetics of the process and, that in turn, responds to changes in the chemical system, becoming an active agent of the process. Treating the full system, reacting region plus environment, on an equal footing quantum mechanical basis for a full exploration of the configurational space is out of reach even today, except for limited applications in relatively small systems. ¹² As discussed below, this limitation could be alleviated in the near future with the aid of Artificial Intelligence. ^{13 , 14}

The participation of the protein environment in the chemical reaction can be modelled using different strategies. Even if we have already introduced QM/MM methods, because of historical reasons, we will follow here an order based in the complexity of the models. A first approach involves simplifying the full protein–ligand system into a minimal model that includes only the atoms directly involved in bond breaking and formation, along with the nearest neighbours that significantly influence the energetics of the process. The so-called quantum chemical cluster approach has been successfully used to unravel complex enzymatic reaction mechanisms, allowing the use of high-level quantum chemistry methods that would not be affordable in other models. ¹⁵ Cluster models must be necessarily complemented with configurational restrictions to avoid that the active site configuration falls apart in the absence of the rest of the system (protein, solvent, counterions,…). For this purpose, the coordinates of some atoms, typically Cα atoms, are frozen at their x-ray values. Obviously, the drastic simplifications inherent in these models, including the neglect of long-range electrostatic effects and a limited protein flexibility, inevitably come at a cost. In some cases, cluster models are embedded into a continuum model, with low dielectric constants mimicking protein hydrophobic cores, in an attempt to capture long-range electrostatic effects. ¹⁶ However, cluster models do not generally allow capturing fine effects such as the structural consequences of mutations on the protein backbone or changes in the conformational diversity of the protein.

The cluster model is usually employed in combination with the harmonic version of Transition State Theory (TST) to calculate rate constants or the impact of changes and modifications on the rate constant. ¹⁷ Stationary structures corresponding to reactants, products, transition states (TSs) and possible intermediates are localized on the potential energy surface (PES) and characterized through the calculation of the hessian matrix. Then their partition functions are evaluated using the standard harmonic-rigid rotor approximation. Potential energy differences and partition functions, or alternatively thermal and entropic corrections to the potential energy, can be then used to estimate rate constants. This well-established procedure can introduce some artifacts in the calculation of vibrational frequencies due to the fact that some atoms remain fixed at their initial positions. ¹⁸ This approach also overlooks the rugged nature of the PES in complex systems, which can make predictions based on a single stationary structure insufficient to accurately represent the ensemble averages corresponding to each state. ¹⁹

A better representation of the interplay between the chemical system and the flexible protein environment, while remaining computationally feasible, can be achieved through hybrid QM/MM approaches. There is a wide variety of QM/MM methods available in the literature and the reader is referred to some reviews to learn about their technical details. ^{6 , 9 , 20} Typically, the interaction between the two subsystems is described using a van der Waals energy term, an electrostatic term and, if needed, terms to account for bonding contributions between both subsystems. A defining feature of these methods is the way in which the QM subsystem is embedded into the MM environment. In the mechanical embedding approach, the MM environment does not polarize the QM electron density. The electrostatic interaction between both subsystems is described by means of partial point charges placed on the positions of the QM atoms. These charges can be fixed (sometimes termed as molecular mechanics embedding) or fitted to the electrostatic potential created by the QM subsystem structure in vacuo. In the electrostatic embedding approach, the charges of the MM subsystem enter in the self-consistent-field procedure, allowing for the polarization of the QM subsystem under the influence of the environment. ²¹ This last scheme is highly recommended to describe enzymatic reactions because active sites often contain charged groups that can significantly polarize the electronic density of the reacting subsystem. ^{6 , 22} The next step in the methodological ladder is the polarization embedding, where the polarizability of MM atoms is also included. In this case not only the QM subsystem, but also the MM atoms can respond to the influence of the QM subsystem and other MM atoms. ^{23 , 24} Applications of this last scheme are mostly limited to the analysis of spectroscopic electronic transitions, where the consideration of the electronic response of the solvent to changes in the electronic density of a solute can be important to quantify the transition energies.

QM/MM schemes provide a more realistic and complete representation of the environment, where specific and long-range interactions of the reactive system with the environment can be included. One of the advantages associated with the use of QM/MM schemes is that these hybrid schemes facilitate the use of simulation methods, in particular Molecular Dynamics (MD). QM/MM MD simulations can be used to generate equilibrium and non-equilibrium trajectories of the system under study, providing valuable information about enzymatic reactions. ²⁵ MD simulations can be used to explore many different configurations of the system that could remain inaccessible during the exploration of the PES. Protein configurational changes can take place in the Michaelis complex after substrate binding or during the reaction progress to facilitate the stabilization of the TS. ^{26 , 27} The configurational search can be promoted using enhanced sampling techniques, such as metadynamics, ²⁸ umbrella sampling (US) ²⁹ or accelerated Molecular Dynamics (aMD), ³⁰ to name just a few of the available techniques. ³¹ This conformational sampling makes possible the calculation of ensemble properties, such as the free energy, that can be connected to experimental thermodynamic and kinetic observables. ³² Analysis of QM/MM MD trajectories can also be used to decipher the role of protein structure in catalysis, including subtle effects such as allostery, where a change occurring far from the active site is transmitted through a cascade of conformational changes, ultimately reaching the active site and significantly altering its catalytic efficiency. ³³

Regarding the study of enzymatic reactions, the most obvious application of QM/MM MD simulations is the calculation of the associated free energy profiles. After the selection of an adequate reaction coordinate (ξ), an issue we discuss below, enhanced sampling techniques can be used to force the system to visit the full range of values of this coordinate, from reactant to products. The probability distribution of the reaction coordinate obtained from these biased simulations can be then used to recover the underlying free energy profile (G _ξ ), using for example the weighted histogram analysis method (WHAM) or other reweighting schemes. ^{34 , 35} The calculation of the reaction free energy profile provides a different perspective in the use of TST. First, the transition state (TS) can be variationally optimized. TST overestimates the rate constant because it neglects the possibility of recrossing trajectories once the TS has been surpassed. ³⁶ This error can be minimized placing the TS in the position that minimizes the reaction flux, that is at the top of the reaction free energy profile. Second, the estimated free energy profile is now obtained considering the conformational diversity of the system and without assuming a harmonic behaviour for the vibrational modes. Thus, the rate constant can be directly obtained from the difference between the free energy value at the TS and at the reactants ( ∆ G ξ ‡ ) as: ³⁶

where ω _R is the reaction coordinate frequency at the reactants well and κ _ξ is the transmission coefficient that corrects for the fraction of trajectories that recross the dividing surface defined by ξ = ξ ^‡. The transmission coefficient is usually taken as unity in most of the applications. Deviations from unity can be due to the choice of an incomplete reaction coordinate, which would impose a practical limitation that can be overcome by optimizing the reaction coordinate, and to the complexity of the potential energy of the system, which would impose a fundamental limit to the validity of this theory. As commented below, exhaustive analysis of the limits of TST in enzymatic processes has shown that this theory can be safely used to understand these reactions. ^{37 , 38}

Lessons learned about enzymatic catalysis

Enzymes catalyse chemical reactions by means of electrostatic interactions. The electrostatic environment created by the enzymatic active site has been optimized by evolution to accelerate chemical reactions, selecting the correct residues and placing them at the correct distances and orientations with respect to the reactive fragments. These electrostatic interactions lower the activation free energy with respect to the uncatalyzed process, stabilizing TSs relative to the reactants more than the solvent does. Key elements to explain the electrostatic origin of catalysis are the concepts of preorganization and reorganization, introduced by Warshel. ³⁹ The active site charges and dipoles that interact with the TS are kept together by the protein three-dimensional structure, resulting in an electrostatic environment that is largely independent of the changes taking place in the chemical system. The active site is preorganized for catalysis thanks to the protein structure. Instead, in aqueous solution, water molecules’ dipoles must be reoriented to follow the electronic changes taking place during the chemical reaction, which has an associated free energy cost termed as reorganization. In enzymes, this reorganization is reduced because the electrostatic environment provided by the active site is already configured to optimally accommodate the transition state of the reaction. To achieve this, protein folding must place together some charges and dipoles in a reduced space. Enzymatic active sites are thus not optimized for stability but for catalytic efficiency, resulting in a well-known trade-off between these two properties. ⁴⁰

Due to the long-range nature of electrostatic interactions QM/MM hybrid models are preferred over cluster models to explain the catalytic efficiency of enzymes. While reaction mechanism can often be explored using cluster models, the impact of distal mutations or other subtle structural changes can only be captured with a more realistic modelling of the protein. Continuum models, often used in combination with cluster models, can even result in electrostatic effects contrary to those produced by the protein in a more faithful representation. This is clearly illustrated with the example of S_N2 reactions, as that represented in Fig. 2a. The nucleophilic attack by an aspartate residue on 1,2-dichloroethane is catalysed by the enzyme Haloalkane Dehalogenase (DhlA). For this type of S_N2 reactions it is well-known that an increase in solvent polarity results in a diminution of the reaction rate. This is due to the fact that the solvent reaction field stabilizes more the reactants and products states than the TS, where the charge is more distributed. Figure 2b shows the average electric field created by the solvent on the carbon atom that suffers a nucleophilic attack obtained for reactive trajectories crossing the TS at t = 0 (with t > 0 corresponding to the evolution towards products and t < 0 to reactants). This electric field was computed from QM/MM simulations in aqueous solution and in the active site of an enzyme. ²⁵ The reaction field created in aqueous solution along the nucleophile-leaving group vector acts as a force against the evolution towards the TS, destabilizing this state with respect to reactants and products. Instead, the electric field created by the protein is not a reaction field. QM/MM simulations on DhlA enzyme show how the enzymatic active site is able to provide an electrostatic stabilization of the TS even if this state is less polar than the reactants. ^{25 , 41} The electric field component along the nucleophile-leaving group vector is now much smaller than in water and does not act as a force against the evolution towards the TS. In fact, when the trajectories are close to the TS (−200 fs > t > 200 fs) the electric field created by the enzyme on the carbon atom favours the TS configuration, providing effective stabilization with respect to the reactants. Enzymes must provide this stabilization of the TS without destabilizing the reactants in the active site, otherwise the binding of the substrate could be compromised. In the present example the nucleophile (an aspartic residue) is part of the enzyme structure. In other cases, a cofactor can be recruited to favour substrate binding. ⁴²

Fig. 2:

Electrostatic effects in enzyme catalysis. a) Schematic representation of the S_N2 reaction between aspartate and 1,2-dichloroethane. b) Time evolution of the electric field along the nucleophile-leaving group vector averaged for reactive trajectories in aqueous solution (blue) and in the active site of DhlA (orange) going from reactants (t < 0) to products (t > 0) after crossing the TS at t = 0. Adapted with permission from ref. 25].

Lessons learned about enzyme design

QM/MM calculations have played a fundamental role in understanding enzymatic reactions and guiding the rational design of novel biocatalysts, particularly in the context of de novo enzyme engineering. A prominent example is the case of Kemp Eliminases (KEs), a family of artificial enzymes designed to catalyze the conversion of benzisoxazoles into salicylonitriles, a reaction not catalyzed by natural enzymes (see Fig. 3). The success of KE engineering relied on the use of theoretical enzymes (theozymes) to model an optimal arrangement of active site residues capable of stabilizing the transition state, primarily by electrostatic interactions with the developing negative charge on the oxygen atom of the substrate. This theozyme-based configuration was subsequently used as a blueprint to design surrounding protein scaffolds. The resulting designs were ranked on the basis of the catalytic geometry and the computed binding free energy for the modelled reaction TS. Designed proteins were further optimized through directed evolution, increasing catalytic efficiency by > 200-fold. ⁴³

Fig. 3:

Schematic representation of a kemp elimination reaction in a kemp eliminase enzyme.

Later developments based on X-ray crystallography and MD simulations, such as the engineered HG-3 enzyme, introduced structural modifications to enhance the positioning of the catalytic base to favor substrate binding and to exclude water molecules from the active site. ⁴⁴ Directed evolution then further refined the catalytic efficiency, culminating in the highly active HG-3.17 variant designed by Hilvert and co-workers, which achieved rate constants approaching those of natural enzymes. ⁴⁵ QM/MM approaches demonstrated that the enhanced activity of evolved KE variants was not merely due to improved substrate positioning but also to a more favorable electrostatic environment that lowered activation barriers. This conclusion was supported by linear correlations between activation free energies and the electrostatic potential exerted by the enzyme on the oxygen atom that is negatively charged during the reaction (see Fig. 3), ⁴⁶ reinforcing the notion that electrostatic effects are critical determinants of catalytic efficiency. Beyond understanding natural and designed enzymes, QM/MM calculations have also informed strategies for computational enzyme design. For example, Head-Gordon and co-workers leveraged electric field optimization to predict mutations that enhanced the catalytic performance of a KE variant, demonstrating that computationally guided modifications could substantially improve reaction rates. ^{47 , 48} In these studies, the authors enhanced the catalytic efficiency of a de novo Kemp Eliminase (KE15) by computationally identifying several mutations that were later validated experimentally. These mutations improved transition state stabilization by optimizing both the electric fields and substrate positioning within the active site. Interestingly, the Asp130Lys mutation was suggested after analysis of long-range electrostatic destabilizing effects. These findings underscore the potential of simulations not only to rationalize how enzymes work but also to guide the design of novel catalysts with tailored functionalities. By elucidating how directed evolution enhances catalysis through electrostatic effects on the transition state, QM/MM simulations can contribute to enzyme engineering, offering a powerful tool for developing efficient biocatalysts for industrial and biomedical applications.

Lessons learned about QM/MM methods

As previously discussed, the predominant role of electrostatic interactions makes QM/MM the method of choice for computational studies of enzyme catalysis. QM/MM simulations of enzymatic reactions must strike a balance between two key aspects: the accuracy of the energy function used to describe the chemical transformation, and the extent of sampling required to obtain well-converged thermodynamic properties. In practice, computational cost is the limiting factor, necessitating a careful trade-off between the quality of the hamiltonian and the length of the simulations. Only recently has the advancement of computational hardware and software made it feasible to achieve hundreds of picoseconds of sampling in QM/MM simulations with medium-sized QM subsystems (∼100 atoms) treated at a reasonable DFT or ab initio level. ⁴⁹

Standard applications of QM/MM methods employ DFT or ab initio hamiltonians for the exploration of potential energy surfaces, while QM/MM MD simulations, that require a considerably larger computational effort, are carried out with lower-level energy descriptions for the QM subsystem: semiempirical or tight-binding methods. These methods can introduce severe systematic errors in the evaluation of the relative free energies along the reaction coordinate but they can be sufficient to capture the enzymatic catalytic effect, the difference between the activation free energies obtained for the reaction in aqueous solution and in the enzyme. ⁵⁰ Several strategies have been developed to attenuate systematic errors associated with the use of these lower-level hamiltonians. One possibility is to add a correction to the energy of the QM subsystem obtained as the difference between single-point calculations carried out at low and high QM levels. ⁵¹ Another possibility is the use of specific parameters in low-level hamiltonians developed to describe correctly a particular chemical reaction or type of reactions. This technique has been employed for example to correct the AM1 hamiltonian for the description of the hydride transfer reaction in Dihydrofolate Reductase ⁵² or to improve the DFTB3 description of phosphate hydrolysis reactions. ⁵³

On the sampling side, the use of higher-level QM methods implies a significant computational effort. This can potentially lead to missing some configurations relevant for the process under study. One of the major challenges, even with cheaper semiempirical hamiltonians, is the treatment of chemical reactions that need more than a single geometrical coordinate for their description. Some mechanisms can be followed by sampling along a single distance or a combination of distances. For example, an antisymmetric combination of distances is a good reaction coordinate for many transfer reactions, as the S_N2 example presented in Fig. 2. However, some chemical reactions involve more than a single chemical event. The deprotonation of a nucleophile can be coupled to the nucleophilic attack and to the protonation of the leaving group, as found in the proteolysis mechanism of the Main Protease of SARS-CoV-2 (see Fig. 4). ^{54 , 55} In such a case, proper sampling of the reaction process may involve the use of more than one distinguished coordinate (up to five bond distances are shown in Fig. 4), which increases exponentially the computational cost. The most popular strategy to explore the free energy dependence along a coordinate is Umbrella Sampling. ²⁹ In this method, the full range of possible values of the coordinate is divided into N intervals, each of them being explored in a different simulation or window. These windows are then combined to obtain the full probability distribution of the coordinate and then the associated free energy change. ³⁴ The number of simulations required to explore the d coordinates (dimensions) of a system under study will be approximately N^d. This is known as the curse of dimensionality. Several strategies have been developed to mitigate this problem. Metadynamics is a successful technique to explore multidimensional free energy landscapes at lower costs, but also exponentially depends on the number of coordinates to be explored. ^{56 , 57} One strategy to avoid the curse of dimensionality is the development of methods to trace the minimum free energy path (MFEP). Instead of exploring the whole multidimensional free energy surface, these methods focus on the MFEP region. ^{58 , 59 , 60 , 61} Once the MFEP associated with a particular mechanism is traced, the advance of the system along this path (or path-CV) can be used as an efficient reaction coordinate to collect the sampling needed to trace the free energy profile, reducing the dimensionality of the problem to just one. ^{62 , 63} This is illustrated in Fig. 4 for the acylation reaction of the Main Protease of SARS-CoV-2. While several bond distances are involved in the acylation process, they can be integrated into a single path-CV (denoted as s in panel b).

Fig. 4:

Exploration of complex enzymatic reactions. a) Bond distances involved in the acylation reaction catalysed by the main protease of SARS-CoV-2. B) Evolution of the bond distances along the mininum free energy path. C) Schematic representation of the transition state. Adapted with permission from ref. 54].

Lessons learned about the validity of transition state theory for enzymatic reactions

TST has served as the conceptual framework for interpreting enzymatic reaction rates. The combination of QM/MM simulations for the calculation of the activation free energy along an appropriate reaction coordinate and equation (1) allows the calculation of rate constants and of the effects of several factors on them. TST has been extensively validated in the case of enzyme catalysis, particularly when corrections for quantum effects and dynamical recrossing are properly incorporated. TST has been successfully used to reproduce or predict various kinetic properties, including rate constants, kinetic isotope effects, ^{64 , 65} the impact of point mutations on enzymatic efficiency ^{66 , 67} and the temperature dependence of reaction rates. ^{33 , 68}

In spite of its apparent success, the validity of TST for explaining enzymatic reactivity has been questioned, with some authors proposing that specific enzyme vibrations, named as promoting vibrations, might actively promote or drive the chemical reaction. ⁶⁹ According to this hypothesis, the enzyme’s dynamics – encoded in its structure – could facilitate the reaction in ways not fully captured by TST. Regarding this point it is important to emphasize that TST is a dynamical theory, in which velocities are thermally averaged under the assumption of an equilibrium distribution. In enzymatic active sites, frequent molecular collisions typically ensure that the system relaxes much faster than the average waiting time between reaction events, thereby supporting one of the central assumptions underlying TST. Obviously, this is not to say that enzymes do not promote chemical reactions but rather that protein motions can be adequately incorporated in the framework of TST, either as an ingredient of the reaction coordinate (when the protein explicitly participates in the reaction through formation of a covalent intermediate) or assuming that they are at equilibrium. Such a confusion regarding the validity of the TST for enzymatic processes comes from the fact that TST results are sensitive to the choice of the reaction coordinate, and a poor choice may lead to a conclusion that TST is invalid for a system in hand. ⁷⁰ However, when the reaction coordinate is carefully chosen, the TST was shown to provide excellent descriptions of enzymatic processes even in the cases where the importance of promoting vibrations was hypothesised. ⁷¹

Another feature of enzymatic systems is that any changes in the environment that are required for the reaction to take place are typically slower than the reactive event itself, thus effectively decoupling the slow protein motions from fast (albeit rare) chemical transitions. This can be illustrated with the analysis of the impact of protein electrostatics, a key contribution to catalysis, along the reaction progress. Figure 5 shows the free energy surface for a Claisen reaction, the transformation of chorismate into prephenate catalysed by BsCM enzyme. ⁵⁰ The free energy was explored using as coordinates an antisymmetric combination of the lengths of the bonds broken and formed during the process and the electrostatic potential that the MM environment creates on the ether oxygen, which develops a negative charge during the process. The MFEP shows that protein fluctuations favouring the stabilization of this charge precede TS crossing, which is essentially governed by internal degrees of freedom of the substrate, while the environment can be considered at equilibrium. ⁷¹ The role of protein motions, globally slower than substrate motions leading to the TS, could be relevant in early and late stages of the reaction but not during barrier crossing. ⁷² In other words, the antisymmetric coordinate is sufficient to define a dividing surface that closely approximates the transition state of the reaction, again supporting the validity of TST for such processes.

Fig. 5:

Environmental participation in enzymatic reaction coordinates. a) Transition state for the Claisen rearrangement of chorismate to prephenate. b) AM1/OPLS free energy surface obtained for the reaction in the active site of BsCM as a function of an internal coordinate and the electrostatic potential created by the enzyme on the ether oxygen atom. Isoenergic lines are drawn every 2 kcal mol⁻¹. The dividing surface along the antisymmetric RC is shown in blue. The minimum free energy path is shown as a black dashed line.

In connection with our previous discussion, one of the major challenges in applying TST to enzymatic reactions involves the selection of an appropriate reaction coordinate. Using the variational principle the TS is identified as the maximum along the free energy profile calculated along the selected coordinate, which is critical to ensure the validity of TST assumptions. Enzymatic reactions are highly multidimensional problems, where several chemical events can take place simultaneously (as illustrated in Fig. 4) and where strong intermolecular interactions couple the protein and substrate degrees of freedom of the system. This can make the selection of an adequate reaction coordinate even more difficult. A poorly chosen reaction coordinate can lead to hysteresis and discontinuity problems in the evaluation of the free energy profile using enhanced QM/MM simulations. ⁷³ From a more fundamental perspective, a poorly chosen reaction coordinate can lead to a definition of the TS dividing surface that exhibits a large number of dynamical recrossings, resulting in a transmission coefficient (see Eq. (1)) significantly lower than unity. In that case the transmission coefficient must be evaluated using rare event trajectories ⁷⁴ or Grote-Hynes theory. ⁷⁵ In contrast, when the dividing surface is defined using a ‘perfect’ reaction coordinate, the equicommittor – that is, the set of configurations in phase space where the probability of reaching the product state before returning to the reactant is exactly 0.5 – TST has been shown to accurately predict enzymatic reaction rates, with transmission coefficients exceeding 0.9. ³⁸ The residual recrossings observed even when using the equicommittor as the reaction coordinate reflects the intrinsic complexity of the potential energy surface and indicate that the error associated with the core assumptions of TST in enzymatic systems is minimal. Of course, the practical implementation of TST can still introduce significant inaccuracies. Therefore, major efforts should be directed toward improving free energy calculation methodologies, including enhanced sampling strategies, refinement of the underlying Hamiltonians and the selection of appropriate reaction coordinates.

For enzymatic reactions involving the transfer of light particles such as a proton, a hydrogen atom or a hydride, quantum mechanical effects become particularly important. These quantum effects manifest in two primary forms: zero-point energy contributions and tunnelling. In this case, the classical treatment of the motion along the reaction coordinate assumed in TST must be corrected to account for these effects. Several methodologies have been proposed to introduce these effects into QM/MM simulations. Truhlar and coworkers proposed the inclusion of a multiplying prefactor in the TST expression for the rate constant that accounts for tunnelling, while activation free energies are corrected for zero-point energies. ⁷⁶ Other strategies to include the quantum nature of nuclei motion in QM/MM simulations are obtaining the adiabatic vibrational wave functions solving the time-independent Schrödinger equation ⁷⁷ or quantizing them via centroid path-integral simulations. ^{78 , 79} In connection with the previous discussion, an interesting question is the selection of an adequate reaction coordinate to drive the simulations and that simultaneously allows for a proper quantization of nuclear motions. Recent studies have shown that some coordinates may fail to isolate environmental effects and can bias the description of TSs for H-transfer reactions, affecting the evaluation of some sensitive properties such as kinetic isotope effects. ⁸⁰

The future of quantum methods applied to enzymology. The machine learning era

As discussed in this work, QM/MM simulations have provided a deep understanding of the theoretical principles underlying the extraordinary catalytic efficiency of the enzymes and also of the practical guidelines for rational enzyme design. However, their application has always been hindered by the huge computational cost of the QM potentials needed to describe the chemical transformations during the enzyme lifecycle. To adequately sample the conformational space relevant to an enzymatic process, one would have to perform calculations on the order of 10⁵–10⁶ energy estimates, bringing the total cost easily up to a million CPU hours. More precise approaches, such as coupled cluster, ⁸¹ generally considered to provide “chemical precision” of the resulting energy estimates (errors below 1 kcal/mol) are orders of magnitude more expensive and therefore out of reach for QM/MM MD simulations. The high computational cost of QM methods forces researchers to either sacrifice the accuracy, resorting to cheap but approximate semiempirical potentials or to significantly reduce the exploration of the conformational landscape, sometimes bringing the simplification to the extreme: reducing the description of the conformational ensemble to energy estimates of selected structures or employing the so-called cluster models, described above.

A way to overcome the seemingly inevitable compromise between accuracy and computational cost of the QM potentials has recently emerged from the rapidly growing field of Machine Learning (ML). A ML model can be trained on a large dataset of QM calculations to learn the relationship between the molecular structure and the total energy. Once trained, such ML interatomic potential (MLIP) can provide molecular energies and forces significantly faster than the reference QM method without much loss in accuracy, following a scheme such as that represented in Fig. 6. Depending on the reference level of theory, the speed-up could be from 10² for cheap DFT methods to 10⁵ and beyond for the most precise wavefunction-based approaches. ⁸² Although fundamentally being an interpolation, various MLIPs have been introduced that can be applied to chemical compounds that were not present in the training dataset. ^{83 , 84 , 85 , 86} There is also on-going work on developing generic reactive MLIPs, that can provide a reasonable description of transition states for a wide range of chemical reaction types. ⁸⁷ The need for a large training set is also being addressed: a recently introduced equivariant graph neural network (EqGNN) architecture ^{88 , 89 , 90} showed remarkable data efficiency, providing stable potentials with as few as hundreds of reference QM calculations. ⁹¹ These advancements suggest that ML potentials are on track to become a reliable alternative to QM methods. In their current state, ML potentials are still inferior to MM in terms of computational cost, ^{82 , 92} making it attractive to combine MLIPs with MM forcefields in a hybrid scheme similar to QM/MM. ^{93 , 94 , 95 , 96 , 97} Such “ML/MM” potentials would be particularly useful for biomolecular simulations, where the size of the system, a large variety of the atomic environments and the need for nanosecond-scale simulations makes the description of the entire system with an MLIP problematic. Currently, there are only a very few examples of application of ML/MM potentials to enzymatic reactions, ^{94 , 98 , 99} but given the rapid advances in this field we expect ML/MM to become a common approach to computational studies of enzymatic catalysis in the next few years.

Fig. 6:

Schematic representation of a typical MLIP architecture. The local environment of each atom (R _x ) is converted to a constant-size atomic feature vector (F _x ). The features can be either predefined or learned from the data (e.g. using graph neural networks). The energy of the molecular system (E_mol) is then calculated as a sum of atomic energies (E _x ) calculated from the feature vectors by some ML model (usually a deep neural network or a Gaussian process regression model).

The dramatic decrease of the computational cost offered by ML and ML/MM approaches opens intriguing possibilities. The complexity of biological systems offers an excellent opportunity for the development of accurate and efficient ML potentials to describe systems of high interest. One example of biochemical systems that are currently beyond the reach of computational chemistry are the ones that couple chemical reactivity with molecular motion, such as ATP synthase, myosin and topoisomerases to mention a few. Understanding the mechanism of action of these complex molecular machines requires both an accurate description of electronic rearrangements in the active site and a description of large-scale conformational changes, requiring extended sampling. The computational description of photophysical effects in biosystems, fundamentally quantum-mechanical in nature, will also be accelerated: MLIPs can provide both accurate description of the conformational ensemble and the electronic structure of biochromophores. This accuracy is essential to properly describe the interaction between living matter and light, including such phenomena as photosynthesis and vision. First glimpses of such symbiosis of ML and photobiology are already appearing. ^{97 , 100}

Finally, the availability of much cheaper reactive molecular potentials will allow routine inclusion of nuclear quantum effects (NQE) in the simulations of enzymatic systems. As discussed above, classical treatment of nuclear motion and reaction rates fails in cases where hydrogen atoms are involved in the reaction, which is the case of many enzymatic reactions. For instance, the classical picture completely ignores kinetic isotope effects (KIEs) – the change in the reaction rate upon isotopic substitution of an atom in the substrate. KIEs arise due to zero-point energy and tunnelling effect experienced by the nuclei. These effects can be described by employing path-integral molecular dynamics (PIMD)-based approaches. PIMD and related methods provide quantum statistical properties from a series of coupled simulations with nuclei described classically. ¹⁰¹ Currently, the high computational cost of QM/MM must be multiplied by the number of coupled simulations, making PIMD prohibitively expensive for routine applications to the study of enzymatic reactivity. The superior efficiency of MLIPs and ML/MM compared to QM-based approaches will pave the way for a full quantum treatment of the biochemical systems, leading to a deeper understanding of the importance of quantum phenomena in living organisms.

Conclusions

The use of quantum mechanical methods in enzymatic catalysis has changed our understanding of biological reactivity. Since the excellent work developed by Karplus, Levitt, and Warshel, awarded with the 2013 Nobel Prize in Chemistry, QM/MM methods have become essential for studying reaction mechanisms in complex biological systems. These approaches allow us to model bond-making and bond-breaking events from first principles, while also considering the complex dynamic and electrostatic effects of the surrounding protein environment. This has led to new insights in how enzymes achieve their remarkable catalytic efficiency, often far exceeding the rate of counterpart reactions in solution. Furthermore, QM/MM simulations provide a convenient platform to investigate quantum phenomena such as hydrogen tunnelling, which may play a key role in enhancing enzyme rates, particularly in proton- and hydride-transfer processes. These findings continue to guide the rational design of biomimetic and synthetic catalysts.

QM/MM methods are fundamental for the validation and refinement of enzyme designs, offering detailed insights into how active sites can be optimized and how reaction mechanisms develop within a biological context. These methods allow for a deeper understanding of the catalytic process, enabling the identification of potential inefficiencies and the suggestion of improvements to enhance the catalytic performance of designs. By focusing on these details, QM/MM simulations help prioritize those designs that have higher chances for experimental success, saving both time and resources in the development of new biocatalysts. However, the predictive capabilities of QM/MM remain limited by the complex interplay between enzyme structure, dynamics, and function. To design highly effective biocatalysts, it is essential to integrate quantum mechanical accuracy with a broader understanding of practical factors beyond the chemical step. This includes the stability and expression levels of the protein and its solubility, which are crucial for ensuring that the computationally optimized designs perform effectively at room conditions.

Accurate QM/MM calculations are still computationally demanding, especially when large systems or extensive conformational sampling are involved. One promising solution is the use of machine learning potentials (and their combination with MM models) trained on quantum mechanical data, which can greatly reduce computational cost while keeping chemical accuracy. If these models can be made transferable across related enzymes, they could help explore many more enzyme variants with a significant reduction in the computational effort. Looking ahead, continued progress in QM/MM and their combination with machine learning methods will be essential to better understand and engineer enzymes with desired functions. Enzyme catalysis is not only about the local chemistry at the active site, but also about how the entire protein environment shapes and supports the reaction. Capturing this complexity more accurately will bring us closer to designing enzymes as efficient and versatile as those evolved by nature.