Impact of Magnetic Field on Mixed Convective Peristaltic Flow of Water Based Nanofluids with Joule Heating

1 Introduction

Low thermal conductivity to common fluids such as water, oil, ethylene glycol mixture has persuaded scientists to look for techniques to enhance heat transfer in such fluids. Experiments have shown that particles of metals possessing size of about 100 nm when suspended in these fluids are more than helpful for this purpose. The mixture obtained by suspending nanoparticles in base fluid is known as nanofluid. At present the nanofluids are readily used in engineering, electrical, and medical sciences. Recent heating and cooling systems, batteries of electronic devices, hyperthermia, cryosurgery, modern drug delivery systems, etc., depend greatly on nanofluids. This is just the beginning as the science of nanofluid dynamics came to light only during the past decade. Motivated researchers have lately shown key interest in finding new ways to utilise nanofluids for energy conservation in many engineering and electric appliances. Brinkman [1] computed the effective viscosity of a two-phase flow model. Results of Brinkman were found in good agreement with the experimental results of nanofluids in a study by Xuan and Li [2] (see Tiwari and Das [3]). Despite of studies previously available on two phase flow models, the term nanofluid was introduced by Choi [4] for the first time while looking for a way to enhance the thermal conductivity of fluids. Afterwards several investigations were carried out to examine the flow behaviour and heat transfer characteristics of nanofluids. Among these the works of Xuan and Li [5], Khanafer et al. [6], Buongiorno [7], and Tiwari and Das [3] are worth mentioning. Several other studies investigating the nanofluid flow can be seen through additional studies [8–16]. Movement of electrically conducting fluid under the influence of an applied electric/magnetic field is strongly influenced by electromagnetic forces. Under such considerations Lorentz force resulting from the interaction of fluid and an applied electric/magnetic field largely perturbs the fluid flow. An externally imposed magnetic field is also a widely used tool for control of melt flows in the bulk crystal growth of semiconductors. One of the main purposes of electromagnetic control is to stabilise the flow and suppress oscillatory instabilities which degrades the resulting crystal. The primary geophysical problem is planetary magnetism produced by currents deep in the planet. Recently, significant attention has also been focused on new applications of magneto-hydrodynamics in metallurgical processing. Taking into account such motivations Sheikholeslami et al. [17, 18] investigated the influence of an applied magnetic field on the transport of nanofluids.

Flows in a channel/tube induced by sinusoidal waves propagating along the channels walls are known as peristaltic flows. These flows find applications in transport of urine, bile, food, chyme, and male and female reproductive cells through their respective tracks in physiology. Engineering applications of such flows can also be seen in roller and finger pumps, heart lung and dialysis machines, hose pumps, and in transport of corrosive and sensitive fluids. One major advantage of peristaltic flows is that fluid thus being transported is prevented from the contamination caused by the external environment. Subject to such wide occurrence and utility of peristaltic flows, various investigations have been carried out to examine the peristalsis under different flow configurations [19–25]. Peristalsis in the presence of magnetic field is quite prominent, for instance, for bleeding reduction during surgeries, hyperthermia treatment, development of magnetic devices using magnetic particles, drug carriers, and many others. With this motivation the peristaltic transport of fluid subject to the influence of applied magnetic field has been studied [26–30].

It is observed that almost nothing has been said about peristaltic transport of nanofluids. Even the studies available on the peristaltic transport of nanofluids [31–33] are based upon the model proposed in the study [7]. None of the mentioned studies takes into account the effective density, viscosity, and thermal conductivity of nanofluids proposed by Brinkman [1] and Xuan and Li [5]. Abbasi et al. [34, 35] investigated the peristaltic flow of copper-water nanofluid through porous medium and with slip effects respectively using the model proposed by Tiwari and Das [3]. Present investigation provides fundamental analysis of peristaltic transport employing the models of Tiwari and Das [3]. Further, the influence of applied magnetic field on peristaltic transport of water-based nanofluids has been investigated here. In fact, the magnetic nanofluid has both liquid and magnetic properties. Such fluids are useful in applications relevant to modulators, optical switches, optical gratings, and tunable optical fiber filters. Magnetic nanoparticles are important in medicine, cancer therapy, and to guide with magnets the particles up the blood stream to a tumour. The nanofluids have been used in drug delivery, hyperthermia treatment, magnetic cell separation, and contrast enhancement in magnetic resonance imaging. The magnetic nanoparticles, in fact, have been found more adhesive to tumour cells than non-malignant cells. Here, two cases of silver (Ag) and copper (Cu) nanoparticles are used for this analysis. Viscous dissipation, Joule heating, heat generation/absorption, and mixed convection effects are considered. Effective density, viscosity, thermal conductivity, and electric conductivity of the nanofluids are taken into account. Mathematical modelling is presented for long wavelength and low Reynolds number approximations. The resulting coupled system is solved numerically using the shooting method. Physical interpretation of numerical results is given with the help of graphs and tables. Comparison of the results for ordinary water, silver-water, and copper-water nanofluids are provided.

2 Mathematical Analysis

Consider an incompressible water-based nanofluid flowing through a channel of width 2d. Channel walls are maintained at a constant temperature T₀ Heat source/sink Φ is present in the channel which is capable of generating/absorbing heat. Coordinate axes are selected in such a way that the X¯> axis lies along the length of the channel, whereas the Y¯> axis is normal to the X¯> axis. Sinusoidal waves travel along the channel walls with constant speed c. These waves have oscillatory characteristics only in the transverse direction and are responsible for flow generation. Wavelength and amplitude of these waves are given by λ and b, respectively. Geometry of peristaltic walls is of the form

(1)± H¯(X¯,t¯) = ± d ± bcos(2πλ(X¯ − ct¯)) , (1)

where + and – signs represent the upper and lower walls respectively. Constant magnetic field of strength B₀ is applied in the transverse direction. Effects of induced magnetic field are ignored under the low magnetic Reynolds number approximation. Effective density ρ_eff, specific heat C_eff, thermal conductivity K_eff and electric conductivity σ_eff of the nanofluid are given [3, 5, 15–18, 35] by

(2)ρeff = (1 − ϕ)ρf + ϕρp,ߙ(ρC)nf = (1 − ϕ)(ρC)f + ϕ(ρC)p,(ρβ)eff = (1 − ϕ)ρfβf + ϕρpβp, KeffKf = Kp + 2Kf − 2ϕ(Kf − Kp)Kp + 2Kf + ϕ(Kf − Kp)σeffσf = 1 + 3(σpσf − 1)ϕ(σpσf + 2) − (σpσf − 1)ϕ. (2)>

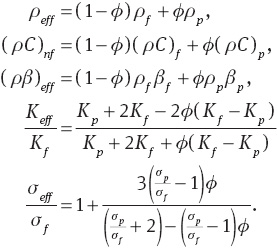
Viscosity of the nanofluid can be obtained by the equations of two-phase flow (see Brinkman [1]):

(3)μeff = μf(1 − ϕ)2.5. (3)

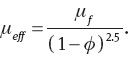
In these equations ρ_f, ρ_p, C_f, C_p, β_f, β_p,σ_f, σ_p,K_f,K_p, μ_f, and ϕ are the density of fluid, density of nanoparticles, specific heat of fluid, specific heat of the nanoparticles, thermal expansion coefficient of fluid, thermal expansion coefficient of the nanoparticles, electric conductivity of fluid, electric conductivity of the nanoparticles, thermal conductivity of fluid, thermal conductivity of the nanoparticles, dynamic viscosity of fluid, and nanoparticles volume fraction, respectively. Numerical values of the thermo-physical properties of water, silver, and copper are given in Table 1 [15–18, 35].

Transformations between the laboratory and wave frames are given by

(4)x¯ = X¯ − ct¯,ߙy¯ = Y¯,ߙߙu¯ = U¯ − c,ߙv¯ = V¯,ߙp¯(x¯,y¯) = P¯(X¯,Y¯,t¯), (4)

in which U¯(X¯,Y¯,t¯),> V¯(X¯,Y¯,t¯)> and P¯(X¯,Y¯,t¯)> are the velocity components and pressure in the laboratory frame. u¯(x¯,y¯),> v¯(x¯,y¯)> and p¯(x¯,y¯)> are the velocity components and pressure in the wave frame, respectively. In light of these mentioned quantities, the conservation laws of mass, momentum, and energy in wave frame become

(5)∂u¯∂x¯ + ∂v¯∂y¯ = 0, (5)

(6)((1 − ϕ)ρf + ϕρp)((u¯ + c)∂∂x¯ + v¯∂∂y¯)(u¯ + c) = − ∂p¯∂x¯ − σeffB02(u¯ + c)+ μf(1 − ϕ)2.5(∂2u¯∂x¯2 + ∂2u¯∂y¯2) + g((1 − ϕ)ρfβf + ϕβpρp) (T − T0), (6)

(7)((1 − ϕ)ρf + ϕρp)((u¯ + c)∂∂x¯ + v¯∂∂y¯)v¯ = − ∂p¯∂y¯+ μf(1 − ϕ)2.5(∂2v¯∂x¯2 + ∂2v¯∂y¯2), (7)

(8)((1 − ϕ)(ρC)f + ϕ(ρC)p)((u¯ + c)∂∂x¯ + v¯∂∂y¯) T = Keff(∂2T∂x¯2 + ∂2T∂y¯2) + Φ + μf(1 − ϕ)2.5[2((∂u¯∂x¯)2 + (∂v¯∂y¯)2)    + (∂u¯∂y¯ + ∂v¯∂x¯)2]+ σeffB02(u¯ + c)2. (8)

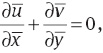
Making use of the following dimensionless quantities

(9)x = x¯λ,ߙߙy = y¯d,ߙu = u¯c,ߙv = v¯cδ,ߙδ = dλ,ߙh = H¯d,ߙa = bd,ߙp = d2p¯cλμf,ߙθ = T − T0T0,ߙυ = μfρf,ߙRe = ρfcdμf,ߙM2 = σfμfB02d2,t = ct¯λ,ߙE = c2CfT0,ߙPr = μfCfKf,ߙGr = ρfgβfT0d2μfc,ߙBr = PrE,ߙε = d2ΦT0Kf,ߙu = ∂ψ∂y,ߙv = −∂ψ∂x, (9)

the dimensionless forms of (6–8) are given as follows:

(10)δReA1((u + 1)∂u∂x + v∂u∂y) = −∂p∂x + 1(1 − ϕ)2.5(δ2∂2u∂x2 + ∂2u∂y2) + GrA2θ − M2A3(u + 1), (10)

(11)δ3ReA1((u + 1)∂v∂x + v∂v∂y) = −∂p∂y + δ2(1 − ϕ)2.5(δ2∂2v∂x2 + ∂2v∂y2), (11)

(12)δPrReA4((u + 1)∂θ∂x + v∂θ∂y) = A5(δ2∂2θ∂x2 + ∂2θ∂y2) + ε + Br[2δ2((∂v∂y)2 + (∂u∂x)2) + (δ2∂v∂x + ∂u∂y)2]  + BrM2A3(u + 1)2, (12)

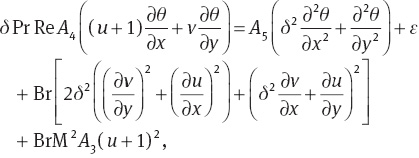
and the continuity equation is identically satisfied. In these equations g, ψ, Re, M, Br, E, Pr, δ, θ and ε are the acceleration due to gravity, stream function, Reynolds number, Hartman number, Brinkman number, Eckret number, Prandtl number, wave number, dimensionless temperature, and the dimensionless heat source/sink parameter, respectively. Applying the long wavelength and low Reynolds number approximations [27–30, 33–35], (10–12) are reduced to the following expressions:

(13)∂p∂x = 1(1 − ϕ)2.5∂3ψ∂y3 + GrA2θ − M2A3(∂ψ∂y + 1), (13)

(14)py = 0, (14)

(15)A5∂2θ∂y2 + Br(1 − ϕ)2.5(∂2ψ∂y2)2 + BrM2A3(∂ψ∂y + 1)2 + ε = 0. (15)

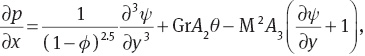
where (14) shows that p ≠ p(y). From (13) and (14) one has

(16)0 = 1(1 − ϕ)2.5∂4ψ∂y4 + GrA2∂θ∂y − M2A3∂2ψ∂y2. (16)

A_1–5 appearing in these equations are given as follows:

(17)A1 = {1 − ϕ + ϕ(ρpρf)}, A2 = {1 − ϕ + ϕ((ρβ)p(ρβ)f)},A3 = 1 + 3(σpσf − 1)ϕ(σpσf + 2) − (σpσf − 1)ϕ, A4 = {1 − ϕ + ϕ((ρC)p(ρC)f)},A5 = Kp + 2Kf − 2ϕ(Kf − Kp)Kp + 2Kf + ϕ(Kf − Kp). (17)

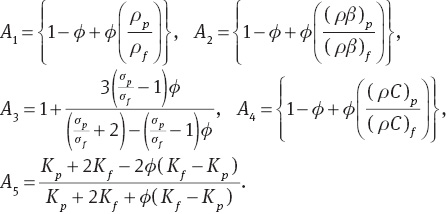
Dimensionless flow rates in the laboratory η(=Q¯cd)> and wave frames F(=q¯cd)> are related by

(18)η = F + 1, (18)

where Q¯,> q¯> are the dimensional flow rates in the laboratory and wave frames and

(19)F = ʃ0h∂ψ∂ydy. (19)

The dimensionless boundary conditions are presented [27, 28] in the forms

ψ = 0,ߙ∂2ψ∂y2 = 0,ߙߙ∂θ∂y = 0, ߙߙatߙy = 0,ψ = F,ߙ∂ψ∂y = −1, ߙߙθ = 0, ߙߙatߙߙy = h.>

Here, h=1 + acos(2πx) is the dimensionless shape of the peristaltic wall. Pressure rise per wavelength (Δp_λ) is defined as follows:

(20)Δpλ = ʃ01(dpdx)dx. (20)

The system of (13–15) subject to boundary conditions (20) is solved numerically using the shooting method in Mathematica. Graphical analysis of the numerical data is presented in the next section.

3 Results and Discussion

The primary goal of this section is to analyze the important physical quantities through graphs and tables. For better presentation, this section is further divided into subsections 3.1, flow behaviour analysis and 3.2, heat transfer analysis. In flow behaviour analysis we present the study of axial velocity, streamlines, pressure gradient, and pressure rise per wavelength. However, the study of temperature profile, maximum fluid temperature, and heat transfer rate at the wall is presented in heat transfer analysis.

3.1 Flow Behaviour Analysis

Axial velocity for variation in nanoparticle volume fraction is examined in Figure 1. This figure shows that velocity traces a parabolic path. Velocity attains maximum value at the centre of the channel. Increase in nanoparticle volume fraction largely decreases the velocity of the nanofluid at the centre of channel, whereas near the channel walls the velocity increases with increase in ϕ. Moreover, copper-water nanofluid possesses a relatively higher velocity near the channel walls when compared to that of silver water nanofluid. Numerical values of the maximum velocity at the centre of the channel for variation in different parameters are provided in Table 2. Comparison of the maximum velocity for ordinary water, silver-water, and copper-water nanofluid is also provided through this table. It is clear from Table 2 that water without nanoparticles possesses greater velocity at the centre of the channel. Silver-water nanofluid owns a higher velocity at the centre of the channel than that of copper-water nanofluid. Velocity at the centre line increases with an increase in Grashoff number, strength of heat source, and Brinkman number. Such increase is larger in the case of water without nanoparticles. However, velocity at the centre decreases with increase in Hartman number. This is due to the resistive nature of the Lorentz force.

Figure 1

Velocity profile for variation in nanoparticle volume fraction when Gr=4.0, a=0.8, x=1, M=1.0, Br=0.3, η=0.8, and ε=2.0.

Table 2

Velocity at the centre line for variation in different parameters when a=0.8, x=1, and η=0.8.

Gr	M	ϵ	Br	u(0) for 10 % Ag	u(0) for 10 % Cu	u(0) for ordinary H2O
0.0	1.5	2.0	0.3	0.214374	0.214374	0.216427
1.0				0.337588	0.334460	0.417383
2.0				0.481061	0.473609	0.674122
3.0				0.659275	0.644862	1.080400
3.0	0.5			0.679136	0.668933	1.001350
	1.0			0.670974	0.659024	1.030050
	1.5			0.659275	0.644862	1.080400
	2.0			0.645986	0.628833	1.159540
	1.5	0.0		0.375415	0.370647	0.449318
		1.0		0.514026	0.504763	0.737259
		2.0		0.659275	0.644862	1.080400
		3.0		0.812218	0.791827	1.533040
		2.0	0.0	0.430303	0.425167	0.595204
			0.1	0.492610	0.485451	0.701287
			0.2	0.566830	0.556817	0.846052
			0.3	0.659275	0.644862	1.080400

The effect of an applied magnetic field on streamlines for silver-water and copper-water nanofluids is studied through Figures 2 and 3, respectively. These figures show that for same value of nanoparticle volume fraction, the streamlines for silver-water and copper-water nanofluid are similar. Increase in Hartman number results in a decrease in the size of trapped bolus for both types of nanofluids.

Figure 2

Streamlines (silver-water nanofluid) for variation in Hartman number when Gr=3.0, a=0.4, ϕ=0.1, Br=0.3, η=1.3, and ε=4.0.

Figure 3

Streamlines (copper-water nanofluid) for variation in Hartman number when Gr=3.0, a=0.4, ϕ=0.1, Br=0.3, η=1.3, and ε=4.0.

The impact of Hartman and Grashoff numbers on the pressure gradient is seen in Figure 4a and b, respectively. Figure 4a shows that the pressure gradient decreases with an increase in M in all parts of the channel except for the wider part. An increase in M enhances the pressure gradient in the wider part of channel. Such increase is large for silver-water nanofluid. An increase in Grashoff number results in an increase of pressure gradient throughout the channel (see Fig. 4b). Again, such an increase is large for the case of silver-water nanofluid.

Figure 4

(a, b) Behaviour of pressure gradient for change in M and Gr when a=0.7, ϕ=0.2, Br=0.3, η=0.8, and ε=4.0.

Pressure rise per wavelength versus flow rate for variations in M and Gr is studied through Figure 5a and b. These figuers show that the pressure rise decreases with an increase in the flow rate. Figure 5a depicts that free pumping flux (value of η when Δp_λ=0) decreases with increase in M. In the retrograde pumping region (η<0 and Δp_λ>0) the pressure rise increases for larger M, whereas the situation is reversed in the augmented pumping region (η>0 and Δp_λ<0). An increase in Grashoff number results in an increase in the pressure rise per wavelength (see Fig. 5b).

Figure 5

(a, b) Behaviour of pressure rise per wavelength for change in M and Gr when a=0.7, ϕ=0.2, Br=0.3, and ε=4.0.

3.2 Heat Transfer Analysis

The effect of nanoparticle volume fraction on the temperature profile is seen through Figure 6. It is clear from this figure that an increase in nanoparticle volume fraction yields a decrease in the temperature of fluid. Such a decrease is large for silver-water nanofluid. It is also concluded from this figure that temperature of the nanofluid is maximum at the centre of the channel. Numerical values of maximum temperature of the fluid for variation in several embedded parameters are given in Table 3. Comparison of the maximum temperature of ordinary water, silver-water and copper-water nanofluid is also provided through this table. This table shows that water without nanoparticles possesses higher temperature. Hence, addition of nanoparticles reduces the temperature of fluid justifying the use of nanoparticles as coolants. In most cases the copper-water nanofluid possesses the least temperature. Maximum temperature is seen to increase with an increase in Gr, M, ϵ and Br. The increasing effect of M and Gr on temperature is due to presence of Joule heating and mixed convection. In all of these cases, the temperature of ordinary water rises more than the nanofluids. Copper-water nanofluid with least temperature may serve as a better coolant than silver-water nanofluid. Effects of M, Br and Gr on the heat transfer rate at the wall are analyzed through Figures 7–9, respectively. Again, in these figures, the comparison of heat transfer rate at the wall for ordinary water with nanofluids is presented. Water with no nanoparticles owns least heat transfer rate at the wall. Clearly the addition of nano-sized particles of metals with higher thermal conductivity (e.g., Ag and Cu) facilitates the heat transfer between the fluid and the solid boundary. Silver nanoparticles with thermal conductivity of 429(W/mK) possess a relatively higher heat transfer rate at the wall when compared with copper nanoparticles with thermal conductivity 400(W/mK). Heat transfer rate at the wall increases with an increase in M, Br, and Gr. Such increase is larger for the increase in Br and Gr.

Figure 6

Temperature profile for variation in nanoparticle volume fraction when Gr=4.0, a=0.8, x=1, M=1.0, Br=0.3, η=0.8, and ε=2.0.

Table 3

Temperature at the centre line for variation in different parameters when a=0.8, x=1, and, η = 0.8.

Gr	M	ϵ	Br	θ(0) for 10 % Ag	θ(0) for 10 % Cu	θ(0) for ordinary H2O
0.0	1.5	2.0	0.3	3.85072	3.85105	4.66212
1.0				4.03980	4.03481	4.99645
2.0				4.31487	4.29949	5.5956
3.0				4.73925	4.70191	6.94182
3.0	0.5			3.10948	3.09617	4.47376
	1.0			3.72488	3.70353	5.36212
	1.5			4.73925	4.70191	6.94182
	2.0			6.14105	6.07727	9.40912
	1.5	0.0		1.67088	1.66248	1.81548
		1.0		3.16808	3.14800	4.14878
		2.0		4.73925	4.70191	6.94182
		3.0		6.39622	6.33434	10.6483
		2.0	0.0	2.43289	2.43310	3.24000
			0.1	3.06927	3.06438	4.05176
			0.2	3.81698	3.80154	5.15219
			0.3	4.73925	4.70191	6.94182

Figure 7

Heat transfer at the boundary for variation in Hartman number when a=0.8, x=1, Gr=3.0, ε=2.0, Br=0.3, and η=0.8.

Figure 8

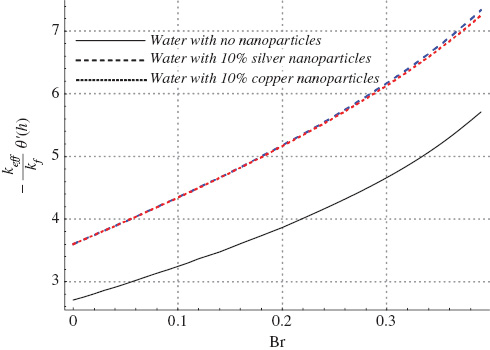
Heat transfer at the boundary for variation in Brinkman number when a=0.8, x=1, Gr=3.0, ε=2.0, M=1.5, and η=0.8.

Figure 9

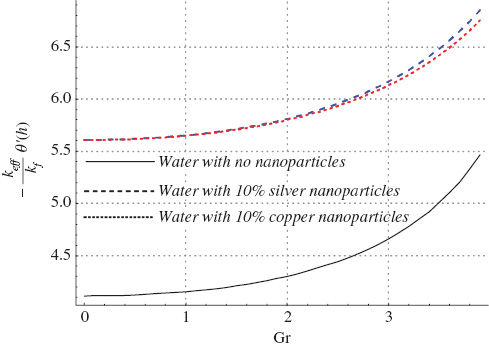
Heat transfer at the boundary for variation in Grashoff number when a=0.8, x=1, Br=0.3, ε=2.0, M=1.5, and η=0.8.

4 Conclusions

The effects of an applied magnetic field on mixed convective peristaltic transport of water-based nanofluids have been studied here. Key findings of this study are as follows.

1. Maximum velocity and temperature of nanofluids is less than that of ordinary water.

2. Maximum velocity and temperature of silver-water nanofluid is relatively higher than copper-water nanofluid.

3. Increase in the strength of applied magnetic field reduces the velocity but it increases the temperature at the centre of the channel.

4. Increase in Grashoff number increases the velocity and temperature.

5. Streamlines of silver-water and copper-water nanofluids are identical.

6. Size of trapped bolus decreases with an increase in magnetic field strength.

7. Heat transfer rate at the wall in the presence of nanofluids is large.

8. Heat transfer rate at the wall increases with the increase in Hartman and Grashoff numbers.