Home Fluorosumanenes as building blocks for organic crystalline dielectrics
Article Publicly Available

Fluorosumanenes as building blocks for organic crystalline dielectrics

  • Yumi Yakiyama EMAIL logo , Minghong Li and Hidehiro Sakurai
Published/Copyright: April 19, 2023
Download Article (PDF)
Pure and Applied Chemistry
From the journal Pure and Applied Chemistry Volume 95 Issue 4

Abstract

Organic crystalline dielectric materials are attractive target in the field of materials chemistry. In their designing strategy, the molecular motion induced by the external dielectric field is required to maximize the polarization effect in the materials to realize a large dielectric constant. Especially, the molecular motion of curved-π aromatics such as C60 and their supramolecular complexes are the known to show characteristic smoothness in the solid state. In this context, we focused on the in-plane motion of the one of the representative buckybowl, sumanene (Sum) in its curve-to-curve-contacted columnar structure as the new platform of the motion for the emergence of dielectric response. The newly designed and synthesized fluorinated sumanene, 1,1-difluorosumanene (F2-Sum), which possesses two fluorine atoms on the same benzylic carbon of pristine sumanene showed a large dipole moment along the in-plane direction. Thermal analyses, variable temperature X-ray diffraction and IR measurements indicated the presence of in-plane motion of F2-Sum although no clear phase transition was involved. This thermal property of F2-Sum realized an anisotropic dielectric response with a Debye-type dielectric relaxation in the single crystalline state. Further trials to form the solid solution of Sum and F2-Sum in various mixing ratio realized the tuning of the dielectric property.

Keywords: Buckybowls; crystal engineering; dielectric response; fluorine; ICPOC-25; sumanene

Introduction

Organic-molecule-based crystalline dielectric materials have recently attracted widespread attention from chemists wishing to develop new organic-electronic devices [1]. In general, such organic-crystalline dielectric materials contain a specific motional unit which responds to the outer electric field change. Various kinds of motional units such as rotor-like structures [2], [3], [4], in-plane motions of planar units in π-stacking columns [5], [6], [7], [8] or supramolecular units [9], and dynamic motions of polar globular molecules [10] are already reported and is known that the molecular motions in the solid state are significantly affected by the molecular structure, in particular, the intermolecular interactions involved in the system.

The molecular motions of curved-π aromatics and their supramolecular complexes often show characteristic smoothness as is confirmed in the isotropic rotation of C60 in the solid state [11] and in a finite single-wall carbon nanotube [12]. This unique feature of curve-to-curve contacts inspired us to use the buckybowls as the new motional units in the crystalline dielectric materials.

Sumanene (Sum) is one of the representative examples of a buckybowl [13] that has unique properties derived from its unusual bowl shape (Fig. 1a) [14]. In particular, Sum forms unidirectionally arranged π-stacking columns in the solid state, in which convex–concave-type curve-to-curve contacts exist [15, 16]. It had already been revealed that the dominant intermolecular interaction present in the crystal packing of Sum are inter- and intracolumnar weak CH–π interactions between benzylic sp2 carbons and the π-bowl, rather than intracolumnar π–π interactions due to the large distance between the two stacking bowls (Fig. 1b). These structural features of Sum are expected to provide a higher flexibility for in-plane motion in the column and to emerge the dielectric response by the introduction of effective responsive moiety to the outer electric field change. In this context, we attempted to introduce F atom directly onto the sumanene skeleton to induce large dipole moment along the in-plane direction (Fig. 1b). Indeed, several elegant works of F-introduced buckybowls have been nicely investigated [17], [18], [19], and especially previously reported 1,1,4,4,7,7-hexafluorosumanene (F6-Sum) gave us a great inspiration that the introduction of F atom onto the sumanene skeleton does not significantly affect its packing pattern [18]. On the basis of this assumption, we have designed and synthesized 1,1-difluorosumanene (F2-Sum), which contains two fluorine atoms on one benzylic carbon of Sum [20]. F2-Sum showed a remarkable anisotropy of the temperature-dependent dielectric response attributable to its in-plane motion in the stacking column. In addition, we realized the tuning of the dielectric property by the formation of solid solution of F2-Sum with Sum in various mixing ratio [21].

Fig. 1: Features of fkuorosumanenes. a) Molecular structures of F2-Sum, Sum and F6-Sum. b) Schematic model of the strategy of this work.
Fig. 1:

Features of fkuorosumanenes. a) Molecular structures of F2-Sum, Sum and F6-Sum. b) Schematic model of the strategy of this work.

Results and discussion

Basic properties of difluorosumanene

The synthesis of 1,1-difluorosumanene F2-Sum was performed by the modified method which was already reported (Scheme 1) [18]. Protection of the carbonyl group of previously reported sumanenen-1-one as a dithioacetal by treatment with butane-1,4-dithiol under the presence of BF3 ·OEt2 gave the product with dithiane ring in 92 % yield. Further fluorination with 2.5 equiv. of NIS and 12.3 equiv. HF·pyridine at −30 °C gave F2-Sum in 77 % yield. Evaluation of F2-Sum using DFT calculation performed at B3LYP/6-31G(d,p) level of theory [22] revealed that the optimized structure of F2-Sum possesses slightly deeper (1.15 Å) than Sum (1.12 Å), but shallower than 3 (1.23 Å). This structural relationship was same in the experimentally obtained single crystal data, and affected the ease of the formation of solid solutions (vide infra). The effect of F introduction of F2-Sum was well reflected in the direction and the magnitude of the dipole moment (Fig. 2).

Scheme 1: Synthesis of F2-Sum.
Scheme 1:

Synthesis of F2-Sum.

Fig. 2: Calculated dipole-moment directions of F2-Sum, Sum, and F6-Sum at the B3LYP/6-31G(d,p) level of theory.
Fig. 2:

Calculated dipole-moment directions of F2-Sum, Sum, and F6-Sum at the B3LYP/6-31G(d,p) level of theory.

The single crystal X-ray analysis of F2-Sum revealed that it affords isostructure of Sum in the crystalline state (Fig. 3). The space group of the crystal 1 was R3c and one third of the structure was the crystallographically independent. The occupancy factor of the two F atoms were 0.33, indicating that the fluorinated benzylic carbon position was randomly disordered in the stacking column to cancel the in-plane dipole (Fig. 3a). The bowl depth of F2-Sum was 1.16 Å, well matching with the calculated value (Fig. 3b). The introduction of F atom induced the expansion of packing parameter (Fig. 3, inset). The bowl-to-bowl distance of F2-Sum is 3.945 Å; this is defined as the distance between the two centroids of the six-membered rings at the bottom of adjacent sumanene skeletons in a stacking column. This value was longer than that for Sum (3.790 Å) [16], however shorter than the case of F6-Sum (4.167 Å) [18]. As seen in the crystals of Sum, the main contributor for the stabilization of the stacking column was CH⋯π-type interactions (3.935 Å) between benzylic carbon atoms and neighbouring aromatic carbon atoms with a partial contribution from F⋯F interactions (2.589 Å), which induced the two closest adjacent column axes to be 9.662 Å (Fig. 3c).

Fig. 3: Crystal structures of F2-Sum. a) Thermal displacement ellipsoid plot of F2-Sum in the crystal structure measured at 100 K and 413 K at 50 % probability. Occupancy factors of F1 and F2 are 0.33 each. b) View from the b axis. c) View from the c axis. Dotted lines: CH···π interactions; solid lines: F–F interactions. Hydrogen atoms are omitted for clarity. The inset table shows the structural parameters of Sum, F2-Sum and F6-Sum. All the parameters were based on single-crystal X-ray analysis data at 100 K.
Fig. 3:

Crystal structures of F2-Sum. a) Thermal displacement ellipsoid plot of F2-Sum in the crystal structure measured at 100 K and 413 K at 50 % probability. Occupancy factors of F1 and F2 are 0.33 each. b) View from the b axis. c) View from the c axis. Dotted lines: CH···π interactions; solid lines: F–F interactions. Hydrogen atoms are omitted for clarity. The inset table shows the structural parameters of Sum, F2-Sum and F6-Sum. All the parameters were based on single-crystal X-ray analysis data at 100 K.

Preparation of solid solutions of F2-Sum and Sum was also performed with different F2-Sum/Sum loading ratios (Table 1). The resulting ratio obtained from 1H NMR and single-crystal X-ray analyses relatively well matched. For further discussion, we used three types of solid solutions in which the loading ratios of F2-Sum/Sum were 83:17 ((F2-Sum)0.83(Sum)0.17), 50:50 ((F2-Sum)0.5(Sum)0.5), and 35:65 ((F2-Sum)0.35(Sum)0.65). It is noteworthy that Sum did not afford solid solutions with F6-Sum due to large structural discrepancies [18]. The resulting solid solutions possessed the same packing pattern as both Sum and F2-Sum, however their cell parameters were markedly changed depending on the F2-Sum/Sum ratio (Table 1). The increment of F atom in the system also gave the larger cell parameter due to the elongation of intermolecular distances caused by the presence of larger F atoms than H atoms. This effect was significant especially in c axis direction and was reasonable to that the substituents projected both the upside and downside of the molecular plane.

Table 1:

Structural parameters of the solid solutions composed of Sum and F2-Sum. The X-ray ratio, bowl depth and bowl-to-bowl distances are the averaged values obtained from the several trials using the different single crystals [21].

Loading ratio (F2-Sum:Sum) X-ray ratio Bowl depth (Å) Bowl-to-bowl distance (Å) Cell parameters (Å)
a and b axes c axis
100:0 [22] 100:0 1.160 3.945 16.735(2) 7.889(2)
87:13 78:22 1.147 3.966 16.755(1) 7.9305(7)
63:37 1.148 3.934 16.723(1) 7.8675(7)
75:25 1.156 3.952 16.740(2) 7.9040(8)
50:50 38:62 1.136 3.867 16.6665(3) 7.7333(2)
46:53 1.143 3.894 16.6836(6) 7.7867(3)
40:60 1.137 3.876 16.6650(5) 7.7508(3)
35:65 11:89 1.117 3.827 16.6264(4) 7.6483(2)
11:89 1.122 3.828 16.6293(5) 7.6551(2)
11:89 1.121 3.825 16.6267(4) 7.6522(2)
0:100 [16] 0:100 1.114 3.790 16.5754(5) 7.5796(5)

Thermal and temperature dependent analysis

As the expected stacking structures were successfully obtained, thermal analyses of F2-Sum were performed to confirm the stability of the materials and to identify the presence of any thermal phase transitions. However, any signs indicating the presence of 1st order phase transition induced by the in-plane molecular rotation were not observed except a peak at around 350 K in the specific-heat measurement of F2-Sum, which indicated the presence of some structural motion that did not affect to overall molecular packing [20].

To clarify the temperature effects to the structure, we performed variable-temperature powder X-ray diffraction analysis (VT-PXRD) (Fig. 4a). In case of F2-Sum, it was confirmed that the total packing pattern was retained in the whole temperature ranges, which was corresponding to the thermal analyses results. However, a sudden change in peak intensity at around 2θ = 25°, corresponding to 202 reflection, was observed at 380 K. The structural analysis revealed that (2 0 2) was placed to slice the stacking column (Fig. 4b). This structural relationship indicated that the intra- and inter-columnar interactions were weakened on heating, followed by faster molecular motion which eventually caused a peak equalization. The single crystal X-ray analysis of F2-Sum at 413 K also showed the elongation of thermal ellipsoid along the in-plane direction while no rotational disorder, indicating the vibration of F2-Sum in the column (Fig. 3a). The possible aspect of F2-Sum at high temperature (>350 K) drawn from those experimental results was with an in-plane pendulum fluctuation in which all the benzylic C–H and C–F bonds continue to have the same types of interactions as those in the low-temperature structure (Fig. 4c). This was further investigated by the variable-temperature IR method (Fig. 5). The absorption data showed slight shifts of a distinct peak spread of around 1030–1200 cm−1 and the ones at around 780–810 cm−1 to a lower-wavenumber region at higher temperatures above 100 °C, which were assignable to a C-F stretching mode and a C–H out-of-plane bending mode, respectively. These observations supported the above discussion derived from the thermal analyses and VT-XRD results.

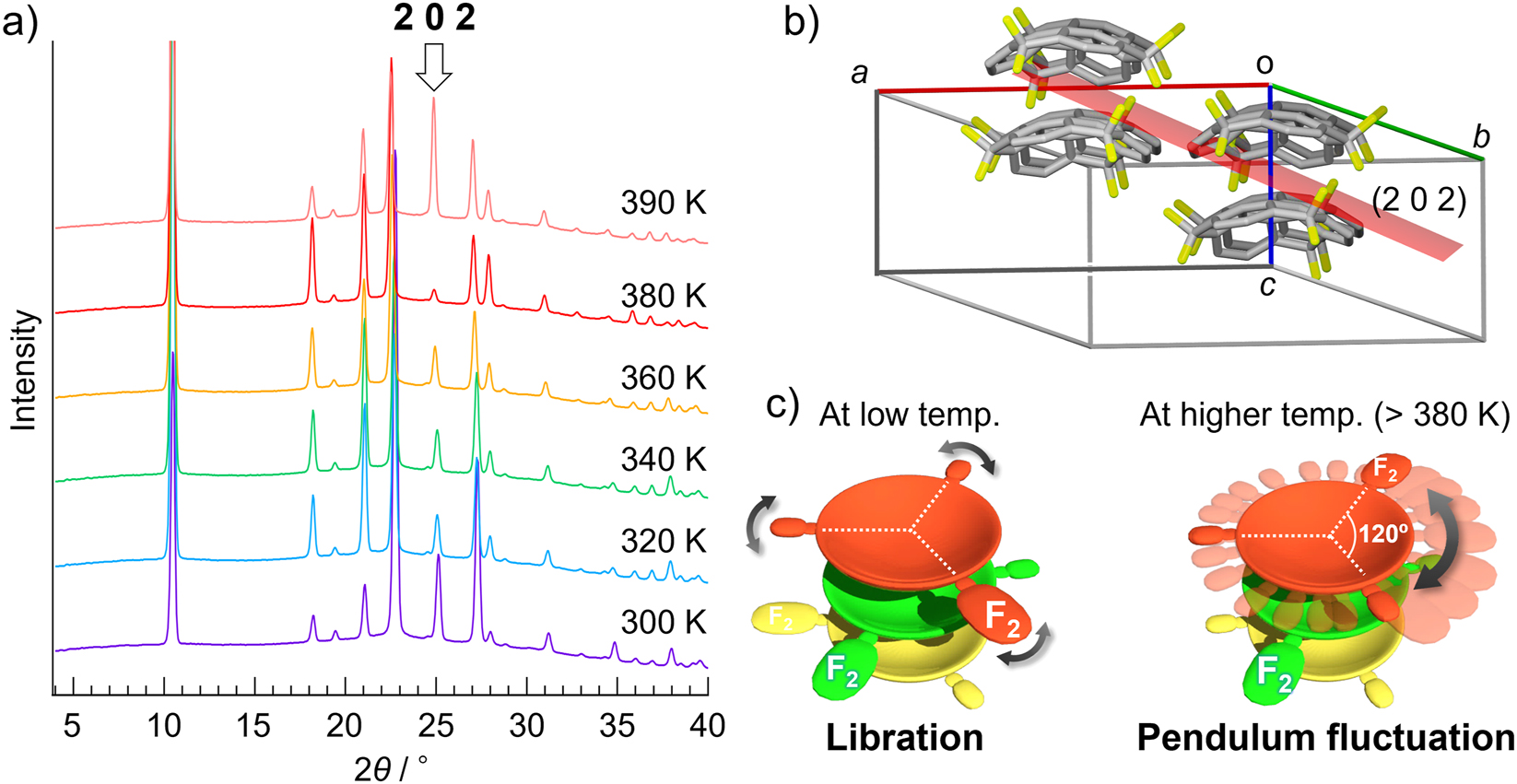
Fig. 4: Dynamic property of F2-Sum in the solid state. a) TD-PXRD patterns of powdered crystalline F2-Sum. Temperature range was from 300 K to 390 K. b) Structural relationship between (2 0 2) plane and the stacking column. c) Schematic representation of the molecular motion in the stacking column of F2-Sum at low and high (>380 K) temperature. The white dotted line shows that the molecular orientation (the position of the three benzylic carbons) is retained in the crystal.
Fig. 4:

Dynamic property of F2-Sum in the solid state. a) TD-PXRD patterns of powdered crystalline F2-Sum. Temperature range was from 300 K to 390 K. b) Structural relationship between (2 0 2) plane and the stacking column. c) Schematic representation of the molecular motion in the stacking column of F2-Sum at low and high (>380 K) temperature. The white dotted line shows that the molecular orientation (the position of the three benzylic carbons) is retained in the crystal.

Fig. 5: VT-IR spectra at C–F stretching (blue) and C–H out-of-plane bending (red) regions of F2-Sum measured at 74 °C ∼ 110 °C. All the data was obtained by using ϕ 7 mm KBr pellet of F2-Sum on a heater-attached Cu plate. Real sample temperature was obtained by using a thermocouple directly attached onto the pellet. All peaks indicated with arrows showed lower wavenumber shift by heating.
Fig. 5:

VT-IR spectra at C–F stretching (blue) and C–H out-of-plane bending (red) regions of F2-Sum measured at 74 °C ∼ 110 °C. All the data was obtained by using ϕ 7 mm KBr pellet of F2-Sum on a heater-attached Cu plate. Real sample temperature was obtained by using a thermocouple directly attached onto the pellet. All peaks indicated with arrows showed lower wavenumber shift by heating.

In the same way, we confirmed that all the thermal experiments result of solid solution samples did not show any sign of the rotational disorder in the measured temperature range, as seen in F2-Sum [21]. However, VT-PXRD analysis of the solid solution samples gave clear insights of the dynamics of the crystal structures. Figure 6 shows the VT-PXRD measurement result for (F2-Sum)0.83(Sum)0.17 sample. A clear low angle shift of the peaks at around 2θ = 23°, 25° and 27.5° (at 310 K) were observed by heating, which were attributable to 10−2, 202 and 3−1−2 reflections, respectively. Meanwhile, the low angle peaks (2−10, 300 and 4−20 reflections) as well as 5−10 reflection were almost intact in whole temperature range. The other two showed the same phenomena [21]. This observation indicated the partial structure change occurred with keeping the total packing structure on heating. Detailed analysis based on the single crystalline data revealed that all the (1 0 −2), (2 0 2) and (3 −1 −2) planes sliced the stacking columns. Meanwhile, all the planes which did not show any shift ((2 −1 0), (3 0 0) and (4 −2 0) planes) were placed parallelly to the column direction (Fig. 6). With considering these experimental results, the expected dynamics of the solid solutions is that the intracolumnar distance extended by heating with keeping the intercolumnar orientations (Fig. 7). As F2-Sum showed the pendulum-like fluctuation, the main possible contributor for the structural dynamics was also F2-Sum and it contributed to the elongation of the intercolumnar molecular distance in the present systems due to its large F atoms.

Fig. 6: Variable temperature PXRD data of the solid solution powder of (F2-Sum)0.87(Sum)0.13 as well as the Lattice plane and the structure relationships.
Fig. 6:

Variable temperature PXRD data of the solid solution powder of (F2-Sum)0.87(Sum)0.13 as well as the Lattice plane and the structure relationships.

Fig. 7: The plausible model of the molecular motion in the solid solution.
Fig. 7:

The plausible model of the molecular motion in the solid solution.

Dielectric measurement of F2-Sum and F2-Sum/Sum solid solutions

As we got clear proof that F2-Sum shows temperature-dependent dynamic property in the crystalline state, we performed the dielectric measurement with using powder crystals (Fig. 8a and e). The experiment revealed that both real (ε 1) and imaginary (ε 2) parts of the dielectric constant were enhanced at above ∼360 K at 1 MHz, with a Debye-type dielectric relaxation. This temperature range was in reasonable agreement with the other experimental observations. The activation energy for the thermally activated motion estimated from the Arrhenius plot of the relaxation time τ versus T p1 −1 was E a = 65 kJ/mol, which was comparable to those of π-planar systems (48–56 kJ/mol) that can be described by an order–disorder model [7, 8].

Fig. 8: Temperature dependence of the a), b), c) and d) real (ε 1) and e), f), g) and h) imaginary (ε 2) parts of the dielectric constants of F2-Sum, (F2-Sum)0.35(Sum)0.65, (F2-Sum)0.50(Sum)0.50, and (F2-Sum)0.87(Sum)0.13, respectively. The applied frequency values were 3.16, 10, 31.6, 100, 316, and 1000 kHz.
Fig. 8:

Temperature dependence of the a), b), c) and d) real (ε 1) and e), f), g) and h) imaginary (ε 2) parts of the dielectric constants of F2-Sum, (F2-Sum)0.35(Sum)0.65, (F2-Sum)0.50(Sum)0.50, and (F2-Sum)0.87(Sum)0.13, respectively. The applied frequency values were 3.16, 10, 31.6, 100, 316, and 1000 kHz.

With the successful observation of the dielectric response of F2-Sum, we also applied the crystalline powders of the three solid solutions to dielectric spectroscopy measurement with the expectation that they show the specific dielectric response depending on the F2-Sum/Sum ratio (Fig. 8b–d, f–h). As we expected, compressed pellet of (F2-Sum)0.87(Sum)0.13 solid solution powder exhibited the most explicit dielectric response; both the real (ε 1) and imaginary (ε 2) parts of the dielectric constant were enhanced at above ∼380 K at 1000 kHz, with a Debye-type dielectric relaxation (Fig. 8b and f). In case of the entries with lower amount of F2-Sum showed a less clear dielectric response (Fig. 8c and g). These differences were clearly reflected in the value of the activation energy for the thermally activated motion; E a = 93 kJ/mol ((F2-Sum)0.35(Sum)0.65), 74 kJ/mol ((F2-Sum)0.5(Sum)0.5), 69 kJ/mol ((F2-Sum)0.87(Sum)0.13), respectively. As pure F2-Sum system gave smallest activation energy among all the samples, it was indicated that the activation energy had the correlation with the change of intermolecular interaction energy depending on the F2-Sum ratio.

Further investigation using a large single crystal of F2-Sum by the two-electrode method clarified the clear contribution of the in-plane motion of F2-Sum for the emergence of dielectric property (Fig. 9). Dielectric measurement under the electric field along the c axis (the solid arrow direction, same as the stacking direction) afforded no clear dielectric response (Fig. 9b). In contrast, the measurement by applying the electric field vertical to the π-stacking axis (dotted arrow direction) showed clear ε 1 and ε 2 responses with a Debye-type dielectric relaxation, as observed in the powder crystal of F2-Sum. The activation energy was 62 kJ/mol for the dielectric relaxation, which was almost the same value as that obtained for the powdered crystalline sample.

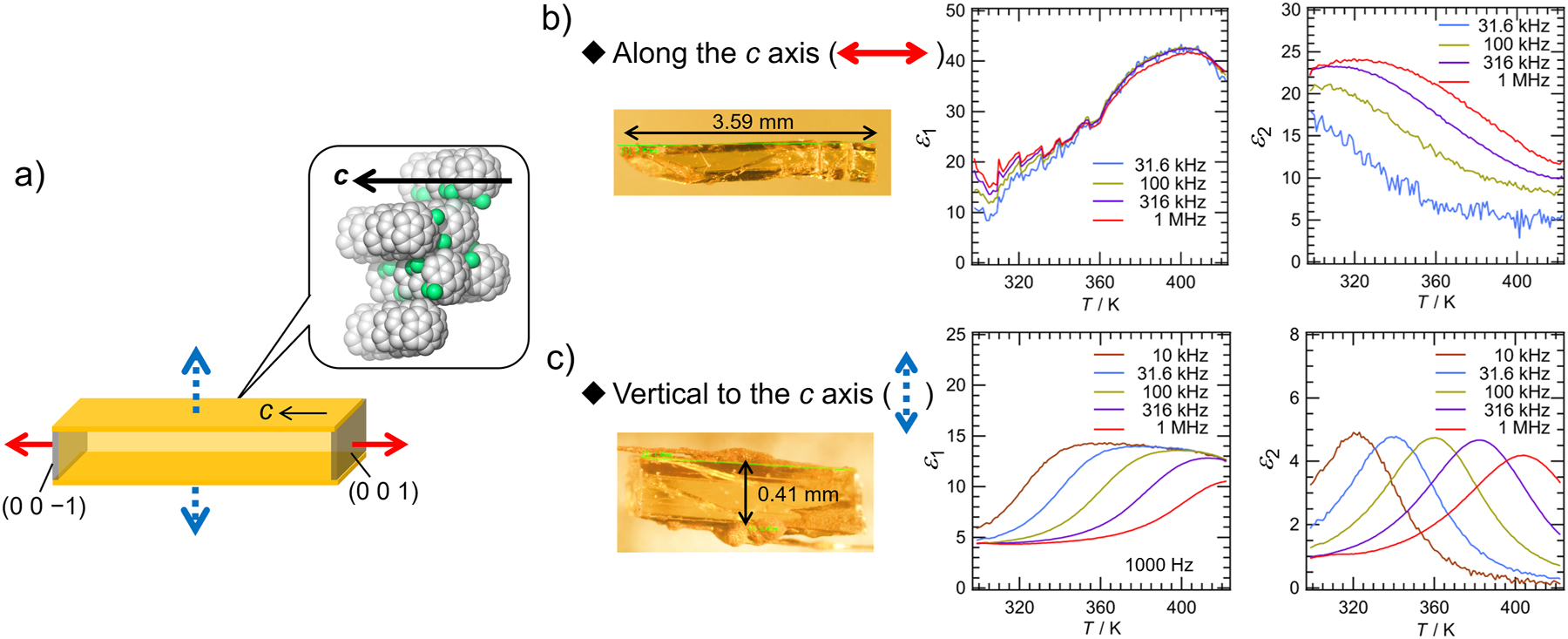
Fig. 9: Investigation of dielectric response of F2-Sum. a) Schematic model of the relationship between the single-crystal shape of F2-Sum and the applied electric field. b) and c) temperature dependence of the real part (ε 1) and the imaginary part (ε 2) of the dielectric constant of F2-Sum in a single-crystalline form measured at various frequencies (31.6, 100, 316, and 1000 kHz for b); 10, 31.6, 100, 316, and 1000 kHz for c)). The direction of the electric field applied for b): parallel to the stacking column; for c): orthogonal to the stacking column. Sample crystal photos are also shown.
Fig. 9:

Investigation of dielectric response of F2-Sum. a) Schematic model of the relationship between the single-crystal shape of F2-Sum and the applied electric field. b) and c) temperature dependence of the real part (ε 1) and the imaginary part (ε 2) of the dielectric constant of F2-Sum in a single-crystalline form measured at various frequencies (31.6, 100, 316, and 1000 kHz for b); 10, 31.6, 100, 316, and 1000 kHz for c)). The direction of the electric field applied for b): parallel to the stacking column; for c): orthogonal to the stacking column. Sample crystal photos are also shown.

Effect of F atom in the interaction energy relationship

Above experiments results, especially the differences of activation energy in each sample, indicated that the dielectric response was strongly affected by both intra- and inter-columnar interactions in each system. In this context, the EDA-FF method interaction energy decomposition analysis performed, which shows the interaction energies based on molecular force field [23, 24]. To make the system simplify, the coordinate of the stacking pair models was extracted from the CIF file of (F2-Sum)0.87(Sum)0.13 sample and all the possible structures of the stacking pairs in the crystals (Sum/Sum, Sum/F2-Sum and F2-Sum/F2-Sum) were considered (Fig. 10) [14]. The calculation indicated that the interaction energy was mainly dominated by the dispersion force in all the case, such as CH···π and π···π interactions. The calculated total energy in intracolumnar Sum/Sum pair was −72.40 kJ/mol, which was larger than that of F2-Sum/F2-Sum pair (−67.97 (180° rotation), −68.05 (60° rotation) kJ/mol) (Fig. 10, inset table). Meanwhile, the value changed depending on the stacking order in case of Sum/F2-Sum pair (−66.67 and −73.03 kJ/mol). Although the one orientation showed higher stability than Sum/Sum pair, these results indicated that the presence of F2-Sum reduced intracolumnar interaction energy. In the same way, inter-columnar direction was also investigated with considering a molecule with its closest neighbour in the different column (Fig. 10). It was also indicated that the dispersion force was the main contributor in all the case, and the energy of Sum/Sum pair was −9.22 kJ/mol, which was larger than those of F2-Sum/F2-Sum pairs (−5.38 to −8.95 kJ/mol). The energy values of the inter-columnar Sum/F2-Sum pairs covered from much smaller to slightly larger values than the case of Sum/Sum pair (−4.81 to −9.31 kJ/mol). Although the stabilization effect from the specific molecular orientation with this largest stabilization energy in Sum/F2-Sum pairs (−9.31 kJ/mol), its contribution probably cancelled by the destabilization effect at other orientations with much higher energy. Considering all the calculation results, it was concluded that the increment of the F2-Sum ratio in the co-crystal will result in the smaller intra- and inter-columnar interactions. It is noteworthy that the absolute values of the intra-columnar interaction were at least around 8 times larger than the case of inter-columnar ones. This indicated that the intra-columnar interaction largely affected the dielectric constants of the systems and therefore the increment of the intra-columnar distance by addition of F2-Sum effectively contributed to emerge better dielectric responses.

Fig. 10: Schematic model of the intra-columnar and inter-columnar interacted pairs in the packing structure. The calculation was performed by using the coordinates extracted from the single crystal data of (F2-Sum)0.87(Sum)0.13 solid solution. The intra-columnar and inter-columnar distances were fixed to be 3.95 Å and 9.66 Å, respectively (based on the X-ray result). Rotation angle was also considered in the calculation of F2-Sum/F2-Sum pair, which was defined by the angle between the two difluorinated benzylic carbons.
Fig. 10:

Schematic model of the intra-columnar and inter-columnar interacted pairs in the packing structure. The calculation was performed by using the coordinates extracted from the single crystal data of (F2-Sum)0.87(Sum)0.13 solid solution. The intra-columnar and inter-columnar distances were fixed to be 3.95 Å and 9.66 Å, respectively (based on the X-ray result). Rotation angle was also considered in the calculation of F2-Sum/F2-Sum pair, which was defined by the angle between the two difluorinated benzylic carbons.

Conclusion

We have designed and synthesized a new curved π-conjugated molecule, 1,1-difluorosumanene (F2-Sum), in which two fluorine atoms are present on the same benzylic carbon of sumanene (Sum). On heating, F2-Sum exhibited an in-plane pendulum fluctuation that did not cause a phase transition in the crystalline state. The combination of this unique thermal property and the large dipole moment along the in-plane direction of F2-Sum realized an anisotropic dielectric response with a Debye-type dielectric relaxation in the single-crystalline state. Further investigations using various solid solutions composed of different ratio of Sum and F2-Sum resulted in the successful tuning of their dielectric properties. The detailed structural analyses and theoretical calculations especially focused on the intra- and inter-columnar interactions in all the possible molecular orientations rationalized that the different physical properties depending on the Sum/F2-Sum ratio were relied on their different structural parameters. These results, focusing on the in-plane molecular motion in the π-stacking column of a buckybowl, will help to provide a better understanding of the dynamics of solid-state curved-π systems and will accelerate their application in functional materials.

Corresponding author: Yumi Yakiyama, Division of Applied Chemistry, Graduate School of Engineering, Osaka University, 2-1 Yamadaoka, Suita, Osaka 565-0871, Japan; and Innovative Catalysis Science Division, Institute for Open and Transdisciplinary Research Initiatives (ICS-OTRI), Osaka University, 2-1 Yamadaoka, Suita, Osaka 565-0871, Japan, e-mail:
Article note: A collection of invited papers based on presentations at the 25th International Conference on Physical Organic Chemistry which was held in Hiroshima, Japan on 10–15th July 2022.

Funding source: Japan Society for the Promotion of Science

Award Identifier / Grant number: JP19H00912

Award Identifier / Grant number: JP20H00400

Award Identifier / Grant number: JP21H05232

Award Identifier / Grant number: JP21H05233

Award Identifier / Grant number: JP21H05235

Award Identifier / Grant number: JP21H05563

Award Identifier / Grant number: JP26102002

Funding source: Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials

Award Identifier / Grant number: 20214025

Acknowledgements

We would like to express our sincere gratitude to Dr. Jianyun Wu, Mr. Kohei Sambe, Prof. Tomoyuki Akutagawa (Tohoku University, Japan), Dr. Moon Dohyun (Pohang Accelerator Laboratory (PAL), POSTECH, Korea), Dr. Xi Chen (Northwest Petroleum University, China), Dr. Takashi Kajitani, Prof. Takanori Fukushima (Tokyo Institute of Technology, Japan) and Prof. Kazunari Matsuda (Kyoto University, Japan) for their great contributions to this work.

  1. Research funding: This work was supported by Grant-in-Aid for Scientific Research on Innovative Areas “π Space Figuration” (No. JP26102002), Grant-in-Aid for Transformative Research Areas “Science of 2.5 Dimensional Materials” (Nos. JP21H05232, JP21H05233, JP21H05235), “Hyper-Ordered Structures Sciences” (No. JP21H05563), ”JSPS KAKENHI (JP19H00912, JP20H00400), and Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials (No. 20214025). The X-ray diffraction studies by synchrotron radiation were performed at BL02B1 of SPring-8 (2020A0808) and at the Pohang Accelerator Laboratory (Beamline 2D-SMC), supported by POSTECH (2020-1st-2D-043). The theoretical calculations were performed at the Research Centre for Computational Science, Okazaki, Japan (Project: 22-IMS-C068). Y.Y. is grateful for the support from the program “Initiative for Realizing Diversity in the Research Environment”, Osaka University. M. L. thanks the China Scholarship Council for the support (ID: CSC 201708310115, CSC 201908050056).

References

[1] J. Brebels, J. V. Manca, L. Lutsen, D. Vanderzande, W. Maes. J. Mater. Chem. A 5, 24037 (2017), https://doi.org/10.1039/c7ta06808e.Search in Google Scholar

[2] R. D. Horansky, L. I. Clarke, J. C. Price, T. A. V. Khuong, P. D. Jarowski, M. A. Garcia-Garibay. Phys. Rev. B: Condens. Matter Mater. Phys. 72, 014302 (2005).10.1103/PhysRevB.72.014302Search in Google Scholar

[3] T. Akutagawa, H. Koshinaka, D. Sato, S. Takeda, S. I. Noro, H. Takahashi, R. Kumai, Y. Tokura, T. Nakamura. Nat. Mater. 8, 342 (2009), https://doi.org/10.1038/nmat2377.Search in Google Scholar PubMed

[4] W. Li, C. T. He, Y. Zeng, C. M. Ji, Z. Y. Du, W. Zhang, X. M. Chen. J. Am. Chem. Soc. 139, 8086 (2017), https://doi.org/10.1021/jacs.7b02981.Search in Google Scholar PubMed

(d) M. Tsurunaga, Y. Inagaki, H. Momma, E. Kwon, K. Yamaguchi, K. Yoza, W. Setaka. Org. Lett. 20, 6934 (2018), https://doi.org/10.1021/acs.orglett.8b03087.Search in Google Scholar PubMed

[5] J. I. Ichikawa, N. Hoshino, T. Takeda, T. Akutagawa. J. Am. Chem. Soc. 137, 13155 (2015), https://doi.org/10.1021/jacs.5b08215.Search in Google Scholar PubMed

[6] R. Bhowal, A. A. Balaraman, M. Ghosh, S. Dutta, K. K. Dey, D. Chopra. J. Am. Chem. Soc. 143, 1024 (2021), https://doi.org/10.1021/jacs.0c11459.Search in Google Scholar PubMed

[7] J. Harada, N. Yoneyama, S. Sato, Y. Takahashi, T. Inabe. Cryst. Growth Des. 19, 291 (2019), https://doi.org/10.1021/acs.cgd.8b01418.Search in Google Scholar

[8] J. Harada, M. Ohtani, Y. Takahashi, T. Inabe. J. Am. Chem. Soc. 137, 4477 (2015), https://doi.org/10.1021/jacs.5b00412.Search in Google Scholar PubMed

[9] C. Shi, X. Zhang, Y. Cai, Y.-F. Yao, W. Zhang. Angew. Chem. Int. Ed. 54, 6206 (2015), https://doi.org/10.1002/anie.201501344.Search in Google Scholar PubMed

[10] J. Harada, T. Shimojo, H. Oyamaguchi, H. Hasegawa, Y. Takahashi, K. Satomi, Y. Suzuki, J. Kawamata, T. Inabe. Nat. Chem. 8, 946 (2016), https://doi.org/10.1038/nchem.2567.Search in Google Scholar PubMed

[11] P. A. Heiney, J. E. Fischer, A. R. McGhie, W. J. Romanow, A. M. Denenstein, J. P. McCauleyJr., A. B. SmithIII, D. E. Cox. Phys. Rev. Lett. 66, 2911 (1991), https://doi.org/10.1103/physrevlett.66.2911.Search in Google Scholar

[12] S. Sato, T. Yamasaki, H. Isobe. Proc. Natl. Acad. Sci. U. S. A. 111, 8374 (2014), https://doi.org/10.1073/pnas.1406518111.Search in Google Scholar PubMed PubMed Central

[13] H. Sakurai, T. Daiko, T. Hirao. Science 301, 1878 (2003), https://doi.org/10.1126/science.1088290.Search in Google Scholar PubMed

[14] M. Saito, H. Shinokubo, H. Sakurai. Mater. Chem. Front. 2, 635 (2018), https://doi.org/10.1039/c7qm00593h.Search in Google Scholar

[15] H. Sakurai, T. Daiko, H. Sakane, T. Amaya, T. Hirao. J. Am. Chem. Soc. 127, 11580 (2005), https://doi.org/10.1021/ja0518169.Search in Google Scholar PubMed

[16] S. Mebs, M. Weber, P. Luger, B. M. Schmidt, H. Sakurai, S. Higashibayashi, S. Onogi, D. Lentz. Org. Biomol. Chem. 10, 2218 (2012), https://doi.org/10.1039/c2ob07040e.Search in Google Scholar PubMed

[17] B. M. Schmidt, S. Seki, B. Topolinski, K. Ohkubo, S. Fukuzumi, H. Sakurai, D. Lentz. Angew. Chem., Int. Ed. 51, 11385 (2012), https://doi.org/10.1002/anie.201205757.Search in Google Scholar PubMed

[18] B. M. Schmidt, B. Topolinski, S. Higashibayashi, T. Kojima, M. Kawano, D. Lentz, H. Sakurai. Chem. Eur. J. 9, 3282 (2013), https://doi.org/10.1002/chem.201204622.Search in Google Scholar PubMed

[19] C. Dubceac, Y. Sevryugina, I. V. Kuvychko, O. V. Boltalina, S. H. Strauss, M. A. Petrukhina. Cryst. Growth Des. 18, 307 (2018), https://doi.org/10.1021/acs.cgd.7b01258.Search in Google Scholar

[20] M. Li, X. Chen, Y. Yakiyama, J. Wu, T. Akutagawa, H. Sakurai. Chem. Commun. 58, 8950 (2022), https://doi.org/10.1039/d2cc02766f.Search in Google Scholar PubMed

[21] M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. MontgomeryJr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, D. J. Fox. Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT (2013).Search in Google Scholar

[22] M. Li, J. Wu, K. Sambe, Y. Yakiyama, T. Akutagawa, T. Kajitani, T. Fukushima, K. Matsuda, H. Sakurai. Mater. Chem. Front. 6, 1752 (2022), https://doi.org/10.1039/d2qm00134a.Search in Google Scholar

[23] T. Lu, Z. Liu, Q. Chen. Mater. Sci. Eng. B 273, 115425 (2021), https://doi.org/10.1016/j.mseb.2021.115425.Search in Google Scholar

[24] T. Lu, F. Chen. J. Comput. Chem. 33, 580 (2012), https://doi.org/10.1002/jcc.22885.Search in Google Scholar PubMed

Published Online: 2023-04-19
Published in Print: 2023-04-25

© 2023 IUPAC & De Gruyter. This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. For more information, please visit: http://creativecommons.org/licenses/by-nc-nd/4.0/

Articles in the same Issue

  1. Frontmatter
  2. In this issue
  3. Editorial
  4. Preface for special issue of ICPOC-25 in Hiroshima
  5. Conference papers
  6. Control of chirality inversion kinetics of triple-helical metallocryptands
  7. Cooperativity in molecular recognition of feet-to-feet-connected biscavitands
  8. Bis-periazulene: remaining non-alternant isomer of pyrene
  9. Closed-shell and open-shell dual nature of singlet diradical compounds
  10. Anticancer activity and DNA interaction of bis(pyridyl)allene-derived metal complexes
  11. Reactivity of electrophilic cyclopropanes
  12. m-Quinodimethane-based fused-ring triplet hydrocarbons
  13. White light emission from an upconverted emission based on triplet-triplet annihilation with rose bengal as the sensitizer
  14. Fluorosumanenes as building blocks for organic crystalline dielectrics
  15. Recent advances in developing tetrathiafulvalene analogs of electrode materials: discovery of an in-cell polymerization technique
  16. The current landscape of author guidelines in chemistry through the lens of research data sharing
  17. Role of fiber density of amine functionalized dendritic fibrous nanosilica on CO2 capture capacity and kinetics
https://doi.org/10.1515/pac-2023-0211
Keywords for this article
Buckybowls; crystal engineering; dielectric response; fluorine; ICPOC-25; sumanene

Articles in the same Issue

  1. Frontmatter
  2. In this issue
  3. Editorial
  4. Preface for special issue of ICPOC-25 in Hiroshima
  5. Conference papers
  6. Control of chirality inversion kinetics of triple-helical metallocryptands
  7. Cooperativity in molecular recognition of feet-to-feet-connected biscavitands
  8. Bis-periazulene: remaining non-alternant isomer of pyrene
  9. Closed-shell and open-shell dual nature of singlet diradical compounds
  10. Anticancer activity and DNA interaction of bis(pyridyl)allene-derived metal complexes
  11. Reactivity of electrophilic cyclopropanes
  12. m-Quinodimethane-based fused-ring triplet hydrocarbons
  13. White light emission from an upconverted emission based on triplet-triplet annihilation with rose bengal as the sensitizer
  14. Fluorosumanenes as building blocks for organic crystalline dielectrics
  15. Recent advances in developing tetrathiafulvalene analogs of electrode materials: discovery of an in-cell polymerization technique
  16. The current landscape of author guidelines in chemistry through the lens of research data sharing
  17. Role of fiber density of amine functionalized dendritic fibrous nanosilica on CO2 capture capacity and kinetics
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 17.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/pac-2023-0211/html
Scroll to top button