A comprehensive review of nanofluids with fractional derivatives: Modeling and application

Ming Shen; Hui Chen; Mengchen Zhang; Fawang Liu; Vo Anh

doi:10.1515/ntrev-2022-0496

Enjoy 40% off

academic books on De Gruyter Brill *

Article Open Access

A comprehensive review of nanofluids with fractional derivatives: Modeling and application

Ming Shen , Hui Chen , Mengchen Zhang , Fawang Liu and Vo Anh

Published/Copyright: December 13, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nanotechnology Reviews Volume 11 Issue 1

Abstract

Nanofluids have been widely used as a class of promising working fluids with excellent heat transfer properties. However, the theoretical research on the thermal enhancement mechanism of nanofluids is still in the preliminary stage. Fractional constitutive models provide a new powerful tool to investigate the superior mechanical and thermal properties of nanofluids owing to their advantages in depicting the memory and genetic properties of the system. Fractional nanofluid models have become one of the hot research topics in recent years as better control of flow behavior and heat transfer can be achieved by considering fractional derivatives. The existing studies have indicated that the results obtained by the fractional-order nanofluid model are more consistent with the experimental results than traditional integer-order models. The purpose of this review is to identify the advantages and applications of fractional nanofluid models. First, various definitions of fractional derivatives and correlations of flux utilized in nanofluid modeling are presented. Then, the recent researches on nanofluids with fractional derivatives are sorted and analyzed. The impacts of fractional parameters on flow behaviors and heat transfer enhancement are also highlighted according to the Buongiorno model as well as the Tiwari and Das nanofluid model with fractional operators. Finally, applications of fractional nanofluids in many emerging fields such as solar energy, seawater desalination, cancer therapy, and microfluidic devices are addressed in detail.

Keywords: nanofluid; fractional derivatives; Buongiorno model; Tiwari and Das model

1 Introduction

Nanofluids introduced by Choi [1] have better heat transfer capability than conventional fluids. The anomalous increment of thermal conductivity of nanofluids provides an opportunity to upgrade traditional thermal technology and presents a theoretical challenge to explain their heat transport mechanisms. The specific thermal conductivity of nanofluids makes them attractive as new working fluids in many fields, including solar thermal engineering, cancer treatment, cooling technology, nuclear reactors, and the petroleum industry [2,3,4].

In recent years, the research of nanofluids has become one of the research focuses, as shown in Figure 1. By considering a nanoparticle-fluid relative velocity, Buongiorno [5] proposed a nonhomogeneous nanofluid model incorporating the effects of Brownian diffusion and thermophoresis. Tiwari and Das [6] developed a model to analyze behaviors of nanofluids in terms of the nanoparticle volume fraction. It was assumed that the dispersion of nanoparticles in the base fluid is homogeneous. Nanofluid is treated as a dilute mixture of two phases in the Buongiorno model, while it is regarded as a single-phase flow in the Tiwari and Das model. By using these two classical models, nanofluids under various physical conditions have been investigated [7,8,9, 10,11,12, 13,14].

Figure 1

Number of papers on nanofluids published reports by Web of Science.

The current research mainly adopts integer-order partial differential equation methods, which would not be able to deal with the complex behavior and the memory effect of physical flows. The available literature shows that the nonlocal properties make fractional-order differential operators suitable for describing the global correlation of complex dynamic systems, phenomena, and structures [15,16,17, 18,19]. Fractional calculus has been employed to solve fluid flow problems in various applications [20,21,22]. In addition, the distribution of nano sized nanoparticles in nanofluids exhibits fractal characteristics [23,24,25, 26,27]. Some latest researches [28,29] indicate that the results of fractional-order nanofluid models are significantly more consistent with the experimental data compared with the ones obtained from the integer-order nanofluid models, which makes the research on fractional nanofluids become a new hotspot (Figure 2).

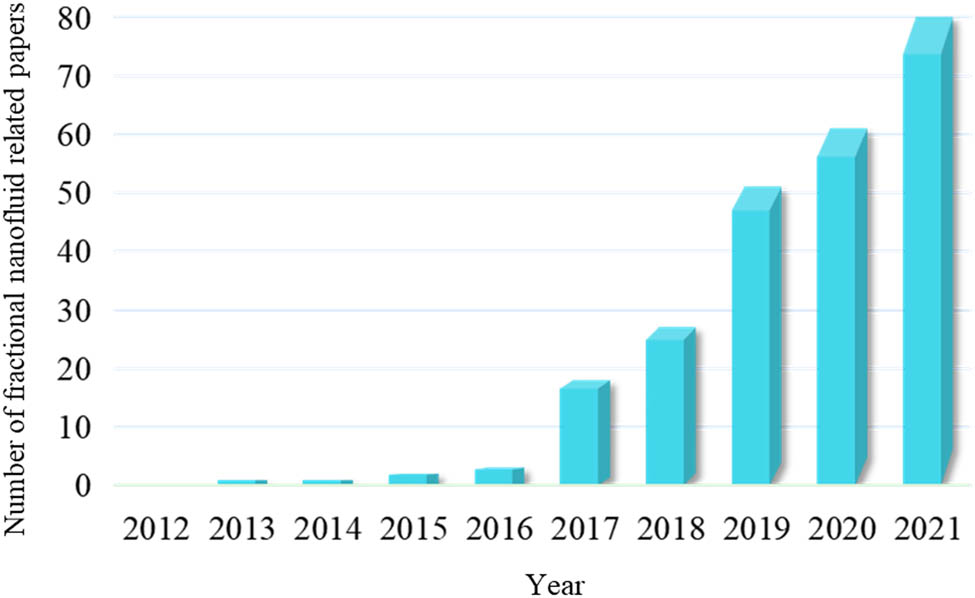
$Figure 2 Number of papers on fractional nanofluids published reports by Web of Science.$

Figure 2

Number of papers on fractional nanofluids published reports by Web of Science.

Recent works on fractional nanofluid models are critically reviewed to gain a better understanding of many key parameters affecting the anomalous heat and nanoparticle diffusion in heat and flow control problems. Section 2 outlines various concepts of fractional derivatives applied in nanofluid models. Section 3 is divided into three subsections. Sections 3.1 and 3.2 the studies on fractional models and physical interpretations of conventional nanofluids, Section 3.3 reviews the works on hybrid nanofluids. A wide range of applications concerning fractional nanofluid models is offered in Section 4. Section 5 draws some conclusions.

2 Various definitions of fractional derivatives

Recently, some new definitions have been proposed considering the nonlocal and nonsingular kernel properties with a good memory effect. This section presents some classical and popular definitions of fractional derivatives applied in describing the physical properties of nanofluids.

2.1 Riemann–Liouville (R–L) derivative

The left-hand and right-hand R–L fractional derivatives with order α ( 0 ≤ α < 1 ) on a finite domain [ a , b ] are given by [30]

(1) D a + α f ( x ) = 1 Γ ( 1 − α ) d d x ∫ a x ( x − ξ ) − α f ( ξ ) d ξ ,

(2) D b − α f ( x ) = − 1 Γ ( 1 − α ) d d x ∫ x b ( ξ − x ) − α f ( ξ ) d ξ ,

respectively. Here, Γ ( ⋅ ) is the Gamma function.

2.2 Caputo derivative

The Caputo derivative is ideal for solving fractional differential equations with initial conditions, which is defined as follows [30]:

(3) D t α C f ( t ) = 1 Γ ( 1 − α ) ∫ 0 t ( t − η ) − α f ′ ( η ) d η .

2.3 Grünwald–Letnikov (G–L) derivative

The G–L derivative is a discrete approximation based on the lattice model with extended-range particle interactions. It can be written as follows [31]:

(4) D t α G L f ( t ) = lim Δ t → 0 1 ( Δ t ) α ∑ m = 0 n ( − 1 ) m α m f ( t − m Δ t ) , t ≥ 0 ,

where α m = α ( α − 1 ) ( α − 2 ) … ( α − m + 1 ) m ! .

2.4 Caputo–Fabrizio (C–F) derivative

The C–F derivative has an extensive application for solving fluid flow problems without singularity [32]. It is defined as follows:

(5) D t α C F f ( t ) = N ( α ) ( 1 − α ) ∫ 0 t exp − α ( t − τ ) 1 − α f ′ ( τ ) d τ ,

where 0 < α < 1 , and N ( α ) is a standardization function that N ( 0 ) = N ( 1 ) = 1 .

2.5 Atangana–Baleanu (A–B) derivative

The A–B derivative has no singularity [33], which is defined by the generalized Mittag–Leffler function as follows:

(6) D t α A B f ( t ) = N ( α ) ( 1 − α ) ∫ 0 t E α − α ( t − τ ) α 1 − α f ′ ( τ ) d τ ,

where 0 < α < 1 and E α ( − t α ) = ∑ k = 0 ∞ ( − t ) α k Γ ( α k + 1 ) is the Mettag–Leffler function.

2.6 Prabhakar derivative

Prabhakar function plays an irreplaceable role in understanding the divergent dielectric properties of disordered materials and heterogeneous structures. Prabhakar derivative is defined as follows [34]:

(7) D α , β , a γ C f ( t ) = ∫ 0 t ( t − τ ) p − β − 1 E α , p − β − γ ( a ( t − τ ) α ) f ( p ) ( τ ) d τ ,

where E α , β γ ( z ) = ∑ n = 0 ∞ Γ ( γ + n ) z n n ! Γ ( γ ) Γ ( α n + β ) , α , β , γ , z ∈ C , and ℜ ( α ) > 0 is the three-parameter Mittag–Leffler function.

2.7 Conformable derivative

The conformable fractional derivative is given by the following form [35]:

(8) D α ( f ) ( t ) = lim ε → 0 , f ( t + ε t 1 − α ) − f ( t ) ε , t > 0 , α ∈ ( 0 , 1 ] ,

where α refers to the order of the fractional derivative. It is shown that this definition is in accordance with the classical definition of polynomial and first-order derivatives for the cases 0 ≤ α < 1 and α = 1 , respectively.

2.8 Constant-proportional Caputo derivative

In 2020, Baleanu et al. [36] reported that the constant-proportional Caputo fractional derivative, which is a combination of R–L and Caputo fractional derivatives, is defined as follows:

(9) D α ( f ) ( t ) = 1 Γ ( 1 − α ) ∫ 0 t [ K 1 ( α ) f ( x ) + K 0 ( α ) f ′ ( x ) ] ( t − x ) − α d x ,

where α is the order.

The fractional-order derivatives of various definitions provide more tools for describing the physical phenomena and heat transfer characteristics of nanofluids and also make it possible for the fractional-order models to go deep into new research fields.

3 Fractional models

It is worth noting that the study of fractional models for nanofluids is still in its infancy due to the complexity of fractional operators. To explain the dramatic augmentation of heat transfer efficiency for nanofluids, increasing attention has been focused on nanofluid modeling by using the fractional derivative. The Buongiorno nanofluid model as well as the Tiwari and Das nanofluid model are two highly cited models for studying the flow and thermal properties of mono and hybrid nanofluids [2]. This section is a comprehensive literature review on investigations by modifying these two models with fractional derivatives and assumptions for different kinds of nanofluids.

3.1 The fractional Buongiorno model for nanofluids

First, the fractional operators were employed to establish the constitutive relationships of viscoelastic fluids [37,38, 39,40]. The fractional flow configuration of a rate-type anomalous nanofluid was studied in ref. [41]. The Caputo fractional derivative was utilized to the velocity field, while the energy and concentration equations were still partial differential equations of integer order described by the Buongiorno model. The finite element method was applied to approximate the velocity, temperature, and concentration fields between two parallel plates. The study of fractional flows of nanofluids has attracted more and more attention due to the development of numerical computation methods for highly nonlinear terms and coupled nonlinear equations. The fractional-order thin film nanofluid flow was considered over an inclined rotating plane [42], where the Caputo derivative was applied to transform the first-order differential equations into a system of fractional differential equations by the Adams-type predictor–corrector method.

Recent researches show that the thermal conductivity of nanofluids cannot be predicted by conventional laws as the suspended particles dramatically augment the thermal conductivity of nanofluids [43]. Shen et al. [44] proposed a renovated Buongiorno model to study Sisko’s nanofluids. The fractional Cattaneo heat conduction in this article [44] was proposed as follows:

(10) q + τ 0 β β ! ∂ β q ∂ t β = − k ∇ T + h p j p ,

where τ 0 denotes relaxation time, and β is the order with β ! = Γ ( 1 + β ) . By using this heat flux, the corresponding energy equation was given as [44]

(11) ( ρ c ) f 1 + τ 0 β β ! ∂ β ∂ t β ∂ T ∂ t + V ⋅ ∇ T = k f Δ T − ∇ h p ⋅ j p + τ 0 β β ! ∂ β ∂ t β ( h p ∇ ⋅ j p ) .

By solving the energy equation numerically, it is shown that the fractional model with Caputo time derivative in Sisko’s nanofluids has a short memory of previous states. It is therefore easy to conclude that the renovated fractional Buongiorno model could be regarded as a candidate model to explore the anomalous heat transport of non-Newtonian nanofluids.

In addition to the time-fractional derivative, the space-fractional derivative has also been used to simulate the nonlocal property of the flow, which means the state depending on the whole region. Whereafter, Zhang et al. [45] provided a new heat conduction as follows:

(12) q + τ 0 β β ! ∂ β q ∂ t β = − k σ γ − 1 ∇ γ T + h p j p , 0 ≤ β < 1 , 0 ≤ γ < 1 ,

where k denotes the thermal conductivity, σ is introduced to maintain the dimensional balance of the constitutive equation, ∂ β / ∂ t β is the Caputo fractional derivative of order β , and for T = T ( t , x , y ) , the operator ∇ γ T is defined as follows [45]:

(13) ∇ γ T = δ ∂ γ T ∂ x γ − ( 1 − δ ) ∂ γ T ∂ ( − x ) γ , δ ∂ γ T ∂ y γ − ( 1 − δ ) ∂ γ T ∂ ( − y ) γ

with δ ( 0 ≤ δ ≤ 1 ) being the weight coefficient. The symbols ∂ γ T ∂ x γ and ∂ γ T ∂ ( − x ) γ are the left and right R–L fractional derivatives of order γ ( n − 1 ≤ γ < n ) . By incorporating this heat conduction, the energy equation could be written as follows [45]:

(14) ( ρ c ) f 1 + τ 0 β β ! ∂ β ∂ t β ∂ T ∂ t + V ⋅ ∇ T = k ∇ ⋅ ( σ γ − 1 ∇ γ T ) − ∇ h p ⋅ j p + τ 0 β β ! ∂ β ∂ t β ( h p ∇ ⋅ j p ) .

By solving this model, it was found that the memory of the heat conduction process could be indicated by the intersection points of concentration profiles, and the heat conduction loss is less. Therefore, this model lays a foundation for further research on the application of fractional calculus in the field of viscoelastic nanofluids.

Anwar [46] analyzed convective phenomena in a nanofluid flow and proposed a new relationship between the energy flux and the diffusion mass flu as follows:

(15) q + τ 1 α Γ ( 1 + α ) ∂ α q ∂ t α = − k ∇ T + h p j p + τ 1 α Γ ( 1 + α ) ∂ α j p ∂ t α ,

where τ 1 and α ( 0 ≤ α < 1 ) represent the relaxation time and the order, respectively. On the other hand, he also applied the operator 1 + τ 1 α Γ ( 1 + α ) ∂ α ∂ t α to the concentration equation given in the Buongiorno model, which is helpful to understand the hereditary and memory characteristics of viscoelastic nanofluids.

In addition, some new definitions of fractional derivatives have been proposed and applied to the study of nanofluids in recent years. Ahmed and Arafa [47] considered a non-Newtonian magnetohydrodynamic nanofluid flow and entropy generation with a Caputo derivative or a conformable derivative in the governing equations over a vertical plate. The results indicated that the Nusselt number is reduced as the order of the fractional derivative approaches one. In another work, Ahmed [48] investigated a natural convection nanofluid flow in wavy walls by using the time and space conformable fractional derivative in the governing equations of the Buongiorno mathematical model. The findings showed that the rate of the nanofluid flow increases as the order of the fractional derivatives decreases. Arafa et al. [49] studied an unsteady magnetohydrodynamic (MHD) nanofluid due to microorganisms using the A–B derivative, which gives a good approximation compared with the Caputo derivative.

It is necessary to note that investigation of the entropy generation optimization for nanofluid models is meaningful due to the wide applications in different systems such as natural convection, evaporative cooling, solar thermal, air separators, microchannel, and so on [50]. So far, little research has been done on entropy generation analysis of nanofluids with fractional derivatives so far. It is believed that this will be a new research hot topic in the near future.

3.2 The fractional Tiwari–Das model for nanofluids

Extending the Tiwari and Das model, the anomalous transport of particles in nanofluids has been described using fractional calculus [51,52]. The thermophysical properties of base fluids and nanoparticles are listed in Table 1.

Table 1

Thermophysical properties of the base fluid and nanoparticles at 20°C [80,86, 101,125, 134]

Base fluid/nanoparticles	ρ (kg/ m 3 )	C p ( J/kg K )	k ( W / m K )	β × 1 0 − 5 ( 1 /K )
Water	997.1	4,179	0.613	21
Ethylene glycol	1,115	2,386	0.2599	3.41 × 1 0 − 8
Blood	1,050	3,617	0.25	0.18
Engine oil	884	1,910	0.114	70
Kerosene oil	783	2,090	0.145	91
Copper (Cu)	8,933	385	401	1.67
Copper oxide (CuO)	6,320	531.8	76.5	1.8
Alumina ( Al 2 O 3 )	3,970	765	40	0.85
Silver (Ag)	10,500	235	429	1.89
Titanium oxide ( TiO 2 )	4,250	686.2	8.9538	0.9
Molybdenum disulfide ( MoS 2 )	5,060	397.21	904.4	2.8424
Gold (Au)	19,300	129	318	1.42
Single wall carbon nanotubes (SWCNTs)	2,600	425	6,600	27
Multi wall carbon nanotubes (MWCNTs)	1,600	796	3,000	44
Graphene	2,200	790	5,000	0.32
Clay	6,320	531.8	76.5	1.80

3.2.1 Nanofluid models with conventional fractional derivatives

To the best of our knowledge, Pan et al. [53] proposed an alternative explanation for the anomalous heat transport of nanofluids by using space fractional derivative first. They concluded that the thermal conductivity of the nanofluid is affected by the motion of non-Newtonian fluids and the nonuniform spatial distribution of nanoparticles. In response, the space-fractional derivative was introduced to model the energy equation given by [53]

(16) u ∂ T ∂ x + v ∂ T ∂ y = k n f ( ρ c p ) n f ∂ β T ∂ y β + Q ( T − T ∞ ) ( ρ c p ) n f ,

where the parameters are given in Table 2 with the subscripts n f , f , and s corresponding to nanofluid, base fluid, and nanoparticle, respectively. The results revealed that the space-fractional temperature equation could be a potential candidate to explain the enhancement of thermal conductivity. Subsequently, they extended the space-fractional thermal transport equation by using the Caputo derivative to describe convective heat transfer in the boundary-layer flow [54] and steady mixed convection of nanofluids [55].

Table 2

Physical properties of nanofluids [56]

Property	Nanofluids
Dynamic viscosity, μ n f	μ f ( 1 − ϕ ) 2.5 , volume fraction ϕ < 0.04
Density, ρ n f	( 1 − ϕ ) ρ f + ϕ ρ s
Heat capacity, ( ρ c p ) n f	( 1 − ϕ ) ( ρ c p ) f + ϕ ( ρ c p ) s
Thermal conductivity, k n f	k s + 2 k f − 2 ϕ ( k f − k s ) k s + 2 k f + ϕ ( k f − k s ) k f

Cao et al. [57] studied a fractional Maxwell nanofluid over a moving plate and formulated the governing equations with Caputo’s definition as follows:

(17) ( 1 + λ 1 α D t α ) ∂ u ∂ t + u ∂ u ∂ x + v ∂ u ∂ y = μ n f ρ n f ∂ 2 u ∂ y 2 − σ B 0 ρ ( 1 + λ 1 α D t α ) u ,

(18) ( 1 + λ 2 β D t β ) ∂ T ∂ t + u ∂ T ∂ x + v ∂ T ∂ y = k n f ( ρ c p ) n f ∂ 2 T ∂ y 2 ,

which were solved numerically by the finite difference method. Their results showed that the order of the time fractional derivative and relaxation time have a noticeable impact on the characteristics of nanofluid flow and heat transfer. Via replacing the time derivative of an integer order with that of fractional order, various nanofluids including Poiselliue/Couette, Maxwell, Oldroyd-B, Jeffrey, and Brinkman have been investigated under different physical conditions [58,59,60, 61,62,63, 64,65,66]. It has been found that the heat transfer rate of fractional nanofluids is better than that of ordinary nanofluids. Furthermore, the influence of nanoparticle shapes on the nanofluid has also been investigated under different physical conditions [67,68, 69,70]. The results indicated that the heat transfer is the strongest for containing spherical nanoparticles, which agrees the physical fact.

Ahmed et al. [71] studied the natural convection heat transfer of nanofluid through a rectangular vertical channel. A thermal process with power-law weakly memory was considered by Povstenko [72], namely,

(19) q = − k n f D t 1 − α ∂ T ∂ y , 0 < α ≤ 1 .

Based on this generalized Fourier law, the convection flow of nanofluids with various nanoparticles between two vertical parallel walls has been investigated [73,74, 75,76]. It indicated that the nanofluid models with fractional generalized Fourier’s law show the memory effect, which could not be demonstrated by the integer-order models.

Asjad et al. [77] considered an MHD viscous nanofluid flow with fractional generalized Newton’s law, fractional generalized Fourier’s law, and Fick’s law with Caputo derivative. The expression for the heat flux q was formulated as the following fractional form:

(20) ( 1 + λ α D t α ) q = − k n f ∂ T ∂ y , 0 < α ≤ 1 .

By using this fractional heat flux, mixed convection magnetohydrodynamics nanofluids [78], viscoelastic nanofluid flow with suspended carbon nanotubes [79], and MHD Maxwell’s nanofluids with SWCNT and MWCNT [80] have been discussed to achieve more control on heat transfer.

In addition, some steady nanofluid models were studied by applying the Caputo derivative to the ordinary differential equation system directly [81,82]. The G–L derivative was also adopted to discuss double rotations between an inner wavy shape and a hexagonal-shaped cavity [83]. The primary outcomes of this work indicated that the double rotation process mainly depends on the time-fractional derivative. To gain a better insight into the memory behavior of nanofluid, the variable-order fractional derivative was implemented in the governing equations to study unsteady natural-convection Jeffrey’s nanofluids over an oscillating plate [84]. Up to now, there have been few studies of variable-order fractional nanofluid models. However, the variable-order fractional calculus is ideal for describing the memory and hereditary properties because that the memory and nonlocality of the system may change with time, space, or other conditions [22]. Therefore, it is notable to mention that further investigations should be dedicated to variable-order fractional nanofluid models.

3.2.2 Nanofluid models with new fractional derivatives

Taking advantage of the C–F derivative, exact analytical solutions were established for the dimensionless temperature and velocity fields of nanofluids over a moving vertical plate [85]. The researchers considered different nanoparticles concluding copper, copper oxide, silver, aluminum, and titanium oxide. Results suggested that the heat transfer enhancement of nanofluids wit Cu was the strongest, while the enhancement effect of nanofluids containing TiO 2 nanoparticles was the weakest. Moreover, the heat transfer is better with spherical nanoparticles than those containing cylindrical nanoparticles, which is in good agreement with experimental results.

Ali et al. [86] considered generalized Couette’s flow of coupled stress nanofluid via the C–F derivative. They revealed that the rate of heat transfer can be increased to 12.38% by adding MoS 2 in regular engine oil. The C–F derivative was also used for thermal analysis in a coaxial cylinder of Oldroyd-B nanofluids [87]. Furthermore, a comparative study between the Caputo and C–F fractional models was presented in the study by Aleem et al. [88] for an MHD nanofluid flow, which showed that the C–F model declines faster than the Caputo model and hence is more suitable to exhibit the flowing memory.

The kernel of the A–B derivative is based on the generalized Mittag–Leffler function without singularity and locality, which gives a better description of memory in different scaled structures. The A–B derivative was applied to study molybdenum disulfide nanofluids with magnetic field and a porous medium [89]. This newly introduced fractional derivative was also applied to study the generalized Brinkman-type nanofluids [90] and convective flow of nanofluids [91]. Many works have followed to investigate nanofluids with this fractional-order derivative [92,90,93, 94,95,96, 97,98,99, 100,101,102]. To have better insight into the various rheological parameters, a comparison of A–B and C–F fractional operators was also performed for temperature and velocity fields of nanofluids with different nanoparticles [103,104,105, 106,107,108, 109,110].

The governing equations of nanofluids have also been modeled using the Prabhakar derivative and the conformable derivative to describe the generalized memory effect recently. For Prabhakar-like thermal transport, carbon nanotube nanofluids [111,112] and Casson nanofluids [113] have been considered. It was found that fractional parameters were meaningful in experimental data fitting in some heating and cooling phenomena. In addition, the conformable fractional derivative was used to study a power-law nanofluid flow [114]. The main outcomes of this study revealed that the increase in the fractional order augments the average Nusselt number regardless of time. From the aforementioned developments, it could be concluded that the fractional solution is more effective than the classical solution.

Because of the advantages these new definitions, it is clear that nanofluid modeling with modeling with new derivatives develops into the growth period. However, some in-depth problems gradually appear. Optimization on the parameters, comparison with experimental data, and analysis of physical phenomena have become their further development shackles, which are theoretical and practical problems that need addressing.

3.3 Fractional models for hybrid nanofluids

Hybrid nanofluids are formed by suspending two or more kinds of nanoparticles in a base fluid [115]. It was found that the thermal characteristics of hybrid nanofluids are better than the base fluid and mono nanofluids [116]. This field has attracted experimental studies [117,118] and theoretical researches [119,120,121, 122,123,124, 125,126,127, 128,129,130]. The general relations of thermophysical properties of hybrid nanofluids are given in Table 3 with the subscripts h n f , f , s 1 , and s 2 corresponding to hybrid nanofluid, base fluid, and two different nanoparticles, respectively.

Table 3

Physical properties of hybrid nanofluids [131]

Property	Hybrid nanofluids
Dynamic viscosity, μ h n f	μ f ( 1 − ϕ s 1 ) 2.5 ( 1 − ϕ s 2 ) 2.5
Density, ρ h n f	( 1 − ϕ s 2 ) [ ( 1 − ϕ s 1 ) ρ f + ϕ s 1 ρ s 1 ] + ϕ s 2 ρ s 2
Heat capacity, ( ρ c p ) h n f	( 1 − ϕ s 2 ) [ ( 1 − ϕ s 1 ) ( ρ c p ) f + ϕ s 1 ( ρ c p ) s 1 ] + ϕ s 2 ( ρ c p ) s 2
Thermal conductivity, k h n f	[ k s 2 + 2 k n f − 2 ϕ s 2 ( k n f − k s 2 ) ] [ k s 1 + 2 k f − 2 ϕ s 1 ( k f − k s 1 ) ] [ k s 2 + 2 k n f + ϕ s 2 ( k n f − k s 2 ) ] [ k s 1 + 2 k f + ϕ s 1 ( k f − k s 1 ) ] k f

To better capture the flow patterns and thermal behaviors of hybrid nanofluids, different fractional derivatives have been employed to model the governing equations. By using the Caputo derivative in constitutive relations, Casson hybrid nanofluids [132,133], hybrid nanofluids with aluminum and copper nanoparticles [134,135], and hybrid Maxwell’s nanofluids [136] have been investigated. Their observations demonstrated that water-based hybrid nanofluids have higher temperature and velocity than engine oil-based hybrid nanofluids, and an increase in the order of the fractional derivative leads to the decrease in both the local and average Nusselt numbers.

The constant-proportional Caputo derivative has been applied to study aluminum and copper hybrid nanofluids due to pressure gradient [137], Brinkman-type hybrid nanofluids holding titanium dioxide and silver nanoparticles [138], as well as MHD free convection flow of hybrid nanofluids with hybridized copper and aluminum oxide nanoparticles [139].

C–F and A–B fractional models were also built for hybrid nanofluids. Gohar et al. [140] considered hybrid nanofluids with Al 2 O 3 and MWCNT nanoparticles using the C–F derivative. Their results showed that the binding strength of cement slurry improves through a sizable increase of suspending hybrid nanoparticles. The C–F fractional derivative has also been applied to investigate a convection flow of water-based hybrid nanofluids with Cu and Al 2 O 3 [141,142] and the MHD hybrid nanofluids with hybridized silver and titanium dioxide in a microchannel [143]. To further analyze the thermal and flow behaviors of hybrid nanofluids, C–F and A–B fractional models were formulated to explain flow patterns and thermal behaviors of sodium alginate-based hybrid nanofluids [144]. The analysis of MHD hybrid nanofluids comprising of MoS 2 and Fe 3 O 4 nanoparticles employing A–B derivative was also presented by Anwar et al. [145]. The observed results implied that the fractional models are more effective for enhancing the heat transfer rate and limiting the shear stress.

In conclusion, various fractional operators have been applied to study the flow and heat mass transfer of mono and hybrid nanofluids. It is necessary to seek the most suitable fractional operators to model the heat and mass transfer properties of nanofluids. To better simulate complex fluid flow and heat and mass transfer of nanofluid, construction of efficient numerical methods and parameter estimation based on experimental data are suggested for future works. It is worth noting that there are few high precision numerical solutions for nonlinear governing equations of fractional nanofluids. So it is necessary to study high-precision numerical methods and their stability and convergence of a general form of nonlinear governing equations for nanofluid models.

Figure 3

Applications of nanofluids.

4 Applications of fractional nanofluids

The increase in thermal conductivity and heat transfer coefficient enables nanofluids attractive as new working fluids or coolants in many emerging applications such as radiators, heat exchangers, aircraft engine cooling, electronic cooling, space shuttle thermal protection, and aircraft environmental control systems [146,3]. Due to memory and the nonlocality property in many complex systems, fractional nanofluids have also shown great potential for applications in some important fields such as solar energy, seawater desalination, human health, and microfluidic devices (Figure 3).

4.1 Solar energy

Solar energy has proved to be free renewable energy with the least effect on the environment. The latest researches have indicated that nanofluids can enhance the collection and heat transfer rate of solar energy [147,148,149].

Nanofluid is regarded as an alternative source to produce solar energy in thermal engineering and solar installations. In an application to solar energy, Aman et al. [150] used the Caputo time fractional derivative to MHD Poiseuille flow of nanofluids with graphene nanoparticles, which showed that fractional nanofluids have a higher rate of heat transfer and Sherwood’s number than ordinary nanofluids. Abro et al. [151] presented a rotating Jeffrey nanofluid model via the C–F fractional operator and considered single, and multi-walled carbon nanotubes. Their results indicated that the incoming sunlight can be absorbed more effectively via introducing a fractional-order operator.

Sheikh et al. [152] carried out a comparative analysis of C–F and A–B fractional models on the application of nanofluids to enhance the performance of solar collectors. In another work, they provided the mathematical formulation for water-based nanofluids with CeO 2 and Al 2 O 3 to increase the heat transfer rate of solar equipment [153]. Considering the influence of the transverse magnetic field, Aamina et al. [154] developed a nanofluid model to predict the heat transport properties of solar collector in a rotating frame. Currently, more and more researchers have paid attention to the application of fractional nanofluid models on solar energy. It is believed that breakthroughs will be made in this area in the near future.

4.2 Water cleaning and desalination

The shortage of fresh water is recognized as one of the global problems to be solved urgently. Many desalination process systems have been developed recently. One of these systems that has attracted much attention is the solar still as it realizes seawater desalination through solar energy [155,156,157]. The implementation of nanofluids provides a promising way to improve the productivity of the solar still. It has been found that the solar still output is greatly affected by nanoparticles such as copper oxide, graphene, and titanium oxide [158,159,160].

Most works related to solar still systems were based on ordinary differential equations, which led to a high error between the numerical and actual values in simulation systems. Until very recently, the fractional derivative has been introduced into modeling solar desalination systems that integrate directly with a photovoltaic panel. El-Gazar Hamdy Hassan et al. [161] studied hybrid nanofluids and saline water preheating using C–F and R–L fractional derivatives. Their results revealed that the best agreement with experimental data was achieved by the R–L derivative with an error of 3.59%, while the error produced by employing the classical derivative reached 18.9%. Utilizing the R–L derivative, they also simulated the thermal performance of solar still on the desalination system [29]. The theoretical results showed an agreement between the proposed fractional model and the experimental data with an error of 1.486% in summer and 3.243% in winter compared to an error of 24.1 and 20.08% in the case of applying the integer-order derivative. Researchers have begun to notice that this method is very efficient in dealing with desalination problems.

4.3 Human health

For the majority of patients, cancer is fatal. Recent investigations indicate that gold nanoparticles can penetrate widely throughout the body. More importantly, gold nanoparticles are capable of producing heat for tumor-selective photothermal therapy and cancer treatment [162,163].

In 2018, Mekheimer et al. [164] studied the blood flow containing gold nanoparticles in a gap between two coaxial tubes. The results indicated that the gold nanoparticles are effective for drug delivery systems as they can increase the temperature distribution to destroy cancer cells. Recently, viscoelastic models with fractional-order different equations were chosen to describe blood movements [165]. Currently, there are still very few studies on the application of fractional nanofluid models to cancer treatment for human health. We hope fractional calculus and nanofluid can play a vital role in human health, which is designed to handle some challenging issues in this application.

4.4 Microfluidic devices

Nanofluids in microfluidic systems are considered to have enormous potential because of their superior heat transfer properties [166]. To improve the thermal and electric conductivity of microfluidic systems, electrified nanofluid flow with suspended carbon nanotubes over a stretching sheet was considered by Anwar et al. [79]. The mathematical formulation of the flow problem was modeled with Caputo fractional derivatives to achieve better control of flow behavior and heat transfer.

In various microfluidic devices, currently, the electroosmotic flow is one of the widely used microfluidic driving methods because of the ability to create continuous pulseless flows and eliminate moving parts [167,168,169]. To offer new insights for the nonlinear issues, the fractional Cattaneo model is applied to study the unsteady electroosmotic flow of second-grade hybrid nanofluid through a vertical annulus and microchannel [170,171]. The results showed that the fractional-order parameter provides a crucial memory effect on the velocity and temperature fields. The superiority of fractional model of electroosmotic flow of nanofluids for microfluidic systems has yet to be explored.

5 Conclusion

The current work provides an overview of recent researches and developments on nanofluid models with fractional derivatives. The enhanced thermal conductivity of mono and hybrid nanofluids leads to significant practical and potential applications. The anomalous thermal behavior of these fluids could not be explained by existing theories. On the one hand, this provides a great opportunity for researchers because the new properties encourage studies of new models of heat transfer and efforts to develop a comprehensive theory. On the other hand, the challenge is greater than ever due to the difficulty of matching the theory with experiments. In recent years, fractional calculus has been introduced to study the anomalous thermal behavior of nanofluids. Since fractional derivatives provide greater flexibility for the heat transfer control, recent investigations have witnessed increasing interest and developments of fractional nanofluids models.

During the last few years, many definitions of fractional derivatives have been introduced to describe the physical phenomena and constitutive equations of materials. It has been found that the fractional derivatives may have good memory effect. However, while providing more tools for research on nanofluids, there is also a challenge in choosing which one is more appropriate with experimental data. Currently, in addition to the research work of high-precision numerical algorithm, it is necessary to carry out experimental analysis on heat and mass transfer characteristics of non-Newtonian nanofluids, study the internal laws of the non-Newtonian nanoparticle flow, and explore the physical significance of qualitative analysis of fractional-order parameters through parameter inversion. Practical application of fractional nanofluid models in solar energy, desalination, human health, microfluidic devices, and other emerging fields is also worthy of further exploration and research.

Funding information: This research was supported by the Natural Science Foundation of Fujian Province (Grant no. 2019J01646).
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Choi SUS. Enhancing thermal conductivity of fluids with nanoparticles. Asme Fed. 1995;231:99. Search in Google Scholar

[2] Kasaeian A, Azarian RD, Mahian O, Kolsi L, Chamkha AJ, Wongwises S, et al. Nanofluid flow andheat transfer in porous media: A review of the latest developments. Int J Heat Mass Transfer. 2017;107:778–91. 10.1016/j.ijheatmasstransfer.2016.11.074Search in Google Scholar

[3] Sajid MU, Ali HM. Recent advances in application of nanofluids in heat transfer devices: a critical review. Renewable Sustainable Energy Rev. 2019;103:556–92. 10.1016/j.rser.2018.12.057Search in Google Scholar

[4] Gupta M, Singh V, Kumar R, Said Z. A review on thermophysical properties of nanofluids and heat transfer applications. Renewable Sustainable Energy Rev. 2017;74:638–70. 10.1016/j.rser.2017.02.073Search in Google Scholar

[5] Buongiorno J. Convective transport in nanofluids. J Heat Transfer. 2006;128:240–50. 10.1115/1.2150834Search in Google Scholar

[6] Tiwari RK, Das MK. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int J Heat Mass Transf. 2007;50:2002–18. 10.1016/j.ijheatmasstransfer.2006.09.034Search in Google Scholar

[7] Mahdy A, Ahmed SE. Laminar free convection over a vertical wavy surface embedded in a porous medium saturated with a nanofluid. Trans Porous Med. 2012;91:423–35. 10.1007/s11242-011-9852-4Search in Google Scholar

[8] Nield DA, Kuznetsov AV. Thermal instability in a porous medium layer saturated by a nanofluid: a revised model. Int J Heat Mass Transf. 2014;68:211–4. 10.1016/j.ijheatmasstransfer.2013.09.026Search in Google Scholar

[9] Sheremet MA, Dinarvand S, Pop I. Effect of thermal stratification on free convection in a square porous cavity filled with a nanofluid using Tiwari and Das nanofluid model. Phys E. 2015;69:332–41. 10.1016/j.physe.2015.02.005Search in Google Scholar

[10] Sheremet MA, Pop I, Bachok N. Effect of thermal dispersion on transient natural convection in a wavy-walled porous cavity filled with a nanofluid: Tiwari and Das nanofluid model. Int J Heat Mass Transf. 2016;92:1053–60. 10.1016/j.ijheatmasstransfer.2015.09.071Search in Google Scholar

[11] Ramzan M, Chung JD, Ullah N. Radiative magnetohydrodynamic nanofluid flow due to gyrotactic microorganisms with chemical reaction and non-linear thermal radiation. Int J Mech Sci. 2017;130:1–40. 10.1016/j.ijmecsci.2017.06.009Search in Google Scholar

[12] Lu DC, Farooq U, Hayat T, Rashidie MM, Ramzan M. Computational analysis of three layer fluid model including a nanomaterial layer. Int J Heat Mass Transf. 2018;122:222–8. 10.1016/j.ijheatmasstransfer.2018.01.080Search in Google Scholar

[13] Selimefendigil F, Chamkha AJ. Magneto hydrodynamics mixed convection in a power law nanofluid-filled triangular cavity with an opening using Tiwari and Das nanofluid model. J Therm Anal Calorim. 2019;135:419–36. 10.1007/s10973-018-7037-xSearch in Google Scholar

[14] Reddy MG, Kumar KG. Cattaneo-Christov heat flux feature on carbon nanotubes filled with micropolar liquid over a melting surface: a stream line study. Int Commun Heat Mass Transf. 2021;122:105142. 10.1016/j.icheatmasstransfer.2021.105142Search in Google Scholar

[15] Liu F, Zhuang P, Liu Q. Numerical methods of fractional partial differential equations and applications. China: Science Press; 2015. Search in Google Scholar

[16] Liu F, Zhuang P, Turner I, Anh V, Burrage K. A semi-alternating direction method for a 2-D fractional FitzHugh-Nagumo monodomain model on an approximate irregular domain. J Comput Phys. 2015;293:252–63. 10.1016/j.jcp.2014.06.001Search in Google Scholar

[17] Liu F, Feng L, Anh V, Li J. Unstructured-mesh Galerkin finite element method for the two-dimensional multi-term time-space fractional Bloch-Torrey equations on irregular convex domains. Comput Math Appl. 2019;78:1637–50. 10.1016/j.camwa.2019.01.007Search in Google Scholar

[18] Sun HG, Zhang Y, Baleanu D, Chen W, Chen YQ. A new collection of real world applications of fractional calculus in science and engineering. Commun Nonlinear Sci Numer Simul. 2018;64:213–31. 10.1016/j.cnsns.2018.04.019Search in Google Scholar

[19] Zhang H, Liu F, Chen S, Anh V, Chen J. Fast numerical simulation of a new time-space fractional option pricing model governing European call option. Appl Math Comput. 2018;339:186–98. 10.1016/j.amc.2018.06.030Search in Google Scholar

[20] Cai J, Hu X, Xiao B, Zhou Y, Wei W. Recent developments on fractal-based approaches to nanofluids and nanoparticle aggregation. Int J Heat Mass Transf. 2017;105:623–37. 10.1016/j.ijheatmasstransfer.2016.10.011Search in Google Scholar

[21] Sulochana C, Ashwinkumar GP. Impact of Brownian moment and thermophoresis on magnetohydrodynamic flow of magnetic nanofluid past an elongated sheet in the presence of thermal diffusion. Multidiscip Model Mater Struct. 2018;14:744–55. 10.1108/MMMS-12-2017-0168Search in Google Scholar

[22] Sun H, Chang A, Zhang Y, Chen W. A review on variable-order fractional differential equations: mathematical foundations, physical models, numerical methods and applications. Fract Calc Appl Anal. 2019;22:110.1515/fca-2019-0003Search in Google Scholar

[23] Xu J, Yu B, Zou M, Xu P. A new model for heat conduction of nanofluids based on fractal distributions of nanoparticles. J Phys D Appl Phys. 2006;39:4486–90. 10.1088/0022-3727/39/20/028Search in Google Scholar

[24] Xiao B, Yu B, Wang Z, Chen L. A fractal model for heat transfer of nanofluids by convection in a pool. Phys Lett A. 2009;373:4178–81. 10.1016/j.physleta.2009.09.020Search in Google Scholar

[25] Gharagozloo PE, Goodson KE. Aggregate fractal dimensions and thermal conduction in nanofluids. J Appl Phys. 2010;108:074309. 10.1063/1.3481423Search in Google Scholar

[26] Qi X. Prediction of heat transfer of nanofluid on criticalheat flux based on fractal geometry. Chin Phys B. 2013;22:014402. 10.1088/1674-1056/22/1/014402Search in Google Scholar

[27] Wei W, Cai J, Hu X, Han Q, Liu S, Zhou Y. Fractal analysis of the effect of particle aggregation distribution on thermal conductivity of nanofluids. Phys Lett A. 2016;380:2953–6. 10.1016/j.physleta.2016.07.005Search in Google Scholar

[28] El-Gazar EF, Hassan H, Rabia SI, Zahra WK. Study of the impact of using hybrid nanofluid and saline water preheating on the performance of both integrated solar still and photovoltaic panel using fractional modeling. Eur Phys J Plus. 2021;136:717. 10.1140/epjp/s13360-021-01654-ySearch in Google Scholar

[29] El-Gazar EF, Zahra WK, Hassan H, Rabia SI. Fractional modeling for enhancing the thermal performance of conventional solar still using hybrid nanofluid: Energy and exergy analysis. Desalination. 2021;503:114847. 10.1016/j.desal.2020.114847Search in Google Scholar

[30] Podlubny I. Fractional differential equations. New York: Academic Press; 1999. Search in Google Scholar

[31] Diethelm K. The analysis of fractional differential equations: an application oriented exposition using differential operators of Caputo type. Berlin: Springer Science and Business Media; 2010. 10.1007/978-3-642-14574-2Search in Google Scholar

[32] Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Progr Fract Differ Appl. 2015;1:1–13. 10.18576/pfda/020101Search in Google Scholar

[33] Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm Sci. 2016;2:763. 10.2298/TSCI160111018ASearch in Google Scholar

[34] Polito F, Tomovski Z. Some properties of Prabhakar-type fractional calculus operators. Fract Differ Calc. 2016;6:73–94. 10.7153/fdc-06-05Search in Google Scholar

[35] Khalil R, AlHorani M, Yousef A, Sababheh M. A new definition of fractional derivative. J Comput Appl Math. 2014;264:65. 10.1016/j.cam.2014.01.002Search in Google Scholar

[36] Baleanu D, Fernandez A, Akgul A. On a fractional operator combining proportional and classical diferintegrals. Mathematics. 2020;8:360. 10.3390/math8030360Search in Google Scholar

[37] Koeller RC. Applications of fractional calculus to the theory of viscoelasticity. J Appl Mech. 1984;51:299–307. 10.1115/1.3167616Search in Google Scholar

[38] Bagley RL, Torvik PJ. A theoretical basis for the application of fractional calculus to viscoelasticity. J Rheol. 1983;27:201–10. 10.1122/1.549724Search in Google Scholar

[39] Liu Y, Zheng L, Zhang X. Unsteady MHD Couette flow of a generalized Oldroyd-B fluid with fractional derivative. Comput Math Appl. 2011;61:443–50. 10.1016/j.camwa.2010.11.021Search in Google Scholar

[40] Bazhlekova E, Bazhlekov I. Unidirectional flows of fractional Jeffreys fluids: thermodynamic constraints and subordination. Comput Math Appl. 2017;73:1363–76. 10.1016/j.camwa.2016.12.009Search in Google Scholar

[41] Anwar MS, Rasheed A. Simulations of a fractional rate type nanofluid flow with non-integer Caputo time derivatives. Comput Math Appl. 2017;74:2485–502. 10.1016/j.camwa.2017.07.041Search in Google Scholar

[42] Gul T, Khan MA, Khan A, Shuaib M. Fractional-order three-dimensional thin-film nanofluid flow on an inclined rotating disk. Eur Phys J Plus. 2018;133:500. 10.1140/epjp/i2018-12315-4Search in Google Scholar

[43] Xuan YM, Li Q. Heat transfer enhancement of nanofluids. Int J Heat Fluid Flow. 2000;21:58–64. 10.1016/S0142-727X(99)00067-3Search in Google Scholar

[44] Shen M, Chen L, Zhang M, Liu F. A renovated Buongiornos model for unsteady Sisko nanofluid with fractional Cattaneo heat flux. Int J Heat Mass Transf. 2018;126:277–86. 10.1016/j.ijheatmasstransfer.2018.05.131Search in Google Scholar

[45] Zhang M, Shen M, Liu F, Zhang H. A new time and spatial fractional heat conduction model for Maxwell nanofluid in porous medium. Comput Math Appl. 2019;78:1621–36. 10.1016/j.camwa.2019.01.006Search in Google Scholar

[46] Anwar MS. Numerical study of transport phenomena in a nanofluid using fractional relaxation times in Buongiorno model. Phys Scr. 2020;95:035211. 10.1088/1402-4896/ab4ba9Search in Google Scholar

[47] Ahmed SE, Arafa AM. Impacts of the fractional derivatives on unsteady magnetohydrodynamics radiative Casson nanofluid flow combined with Joule heating. Phys Scr. 2020;95:095206. 10.1088/1402-4896/abab37Search in Google Scholar

[48] Ahmed SE. Effect of fractional derivatives on natural convection in a complex-wavy-wall surrounded enclosure filled with porous media using nanofluids. Z Angew Math Mech. 2020;100:201800323. 10.1002/zamm.201800323Search in Google Scholar

[49] Arafa AAM, Rashed ZZ, Ahmed SE. Radiative MHD bioconvective nanofluid flow due to gyrotactic microorganisms using Atangana-Baleanu Caputo fractional derivative. Phys Scr. 2021;96:055211. 10.1088/1402-4896/abe82dSearch in Google Scholar

[50] Mahian O, Kianifar A, Kleinstreuer C, Al-Nimr M, Pop I, Sahin AZ, et al. A review of entropy generation in nanofluid flow. Int J Heat Mass Transf. 2013;65:514–32. 10.1016/j.ijheatmasstransfer.2013.06.010Search in Google Scholar

[51] Chen W, Zhang J, Zhang J. A variable-order time-fractional derivative model for chloride ions sub-diffusion in concrete structures. Fract Calc Appl Anal. 2013;16;76–92. 10.2478/s13540-013-0006-ySearch in Google Scholar

[52] Sun H, Zhang Y, Chen W, Reeves DM. Use of a variable index fractional derivative model to capture transient dispersion in heterogeneous media. J Contam Hydrol. 2014;157:47–58. 10.1016/j.jconhyd.2013.11.002Search in Google Scholar PubMed

[53] Pan M, Zheng L, Liu F, Zhang X. Modeling heat transport in nanofluids with stagnation point flow using fractional calculus. Appl Math Modell. 2016;40:8974–84. 10.1016/j.apm.2016.05.044Search in Google Scholar

[54] Pan M, Zheng L, Liu F, Liu C, Chen X. A spatial-fractional thermal transport model for nanofluid in porous media. Appl Math Modell. 2018;53:622–34. 10.1016/j.apm.2017.08.026Search in Google Scholar

[55] Pan M, Zheng L, Liu C, Liu F, Lin P, Chen G. A stochastic model for thermal transport of nanofluid in porous media: derivation and applications. Comput Math Appl. 2018;75:1226–36. 10.1016/j.camwa.2017.10.022Search in Google Scholar

[56] Oztop HF, Abu-Nada E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int J Heat Fluid Flow. 2008;29:1326–36. 10.1016/j.ijheatfluidflow.2008.04.009Search in Google Scholar

[57] Cao Z, Zhao. J, Wang Z, Liu F, Zheng L. MHD flow and heat transfer of fractional Maxwell viscoelastic nanofluid over a moving plate. J Molecular Liquids. 2016;222:1121–7. 10.1016/j.molliq.2016.08.012Search in Google Scholar

[58] Fetecau C, Vieru D, Azhar WA. Natural convection flow of fractional nanofluids over an isothermal vertical plate with thermal radiation. Appl Sci. 2017;7:247. 10.3390/app7030247Search in Google Scholar

[59] Aman S, Khan I, Ismail Z, Salleh MZ. Applicataions of faactioanal derivatives to nanofluids: exact and numerical solutions. Math Model Nat Phenom. 2018;13:2. 10.1051/mmnp/2018013Search in Google Scholar

[60] Shen M, Chen S, Liu F. Unsteady MHD flow and heat transfer of fractional Maxwell viscoelastic nanofluid with Cattaneo heat flux and different particle shapes. Chin J Phys. 2018;56:1199–211. 10.1016/j.cjph.2018.04.024Search in Google Scholar

[61] Zhang Y, Jiang J, Bai Y. MHD flow and heat transfer analysis of fractional Oldroyd-B nanofluid between two coaxial cylinders. Comput Math Appl. 2019;78:3408–21. 10.1016/j.camwa.2019.05.013Search in Google Scholar

[62] Roohi R, Heydari MH, Bavi O, Emdad H. Chebyshev polynomials for generalized Couette fow of fractional Jefrey nanofuid subjected to several thermochemical effects. Eng Comput. 2021;37:579–95. 10.1007/s00366-019-00843-9Search in Google Scholar

[63] Hamid M, Zubair T, Usman M, Haq RU. Numerical investigation of fractional-order unsteady natural convective radiating flow of nanofluid in a vertical channel. AIMS Math. 2019;4:1416–29. 10.3934/math.2019.5.1416Search in Google Scholar

[64] Razzaq A. Heat and mass transfer analysis of Brinkman type fractional nanofluid over a vertical porous plate with velocity slip and Newtonian heating. Punjab Univ J Math. 2019;51:45–69. Search in Google Scholar

[65] Saqib M, Ali F, Khan I, Sheikh NA, Khan A. Entropy generation in gifferent types of fractionalized nanofluids. Arabian J Sci Eng. 2019;44:531–40. 10.1007/s13369-018-3342-8Search in Google Scholar

[66] Sheikh NA, Ching DL, Khan I, Ahmad A, Ammad S. Concrete based Jeffrey nanofluid containing Zinc Oxide nanostructures: application in cement industry. Symmetry. 2020;12:1–17. 10.3390/sym12061037Search in Google Scholar

[67] Anwar T, Kumam P, Thounthong P, Sitthithakerngkiet K. Nanoparticles shape effects on thermal performance of Brinkman-typeferrofluid under heat injection/consumption and thermal radiation: a fractional model with non-singular kernel and non-uniform temperature and velocity conditions. J Mol Liq. 2021;335:116107. 10.1016/j.molliq.2021.116107Search in Google Scholar

[68] Anwar T, Kumam P, Shah Z, Sitthithakerngkiet K. Significance of shape factor in heat transfer performance of Molybdenum-Disulfide nanofluid in multiple flow situations:a comparative fractional study. Molecules. 2021;26:3711. 10.3390/molecules26123711Search in Google Scholar PubMed PubMed Central

[69] Madhura KR, Atiwali B, Iyengar SS. Influence of nanoparticle shapes on natural convection flow with heat and mass transfer rates of nanofluids with fractional derivative. Math Meth Appl Sci. 2021;7404:1–17. 10.1002/mma.7404Search in Google Scholar

[70] Saqib M, Khan I, Shafe S, Mohamad AQ. Shape efect on MHD fow of time fractional Ferro-Brinkman type nanofuid with ramped heating. Sci Rep. 2021;11:3725. 10.1038/s41598-020-78421-zSearch in Google Scholar PubMed PubMed Central

[71] Ahmed N, Vieru D, Fetecau C, Shah NL. Convective flows of generalized time-nonlocal nanofluids through a vertical rectangular channel. Phys Fluids. 2018;30:052002. 10.1063/1.5032165Search in Google Scholar

[72] Povstenko Y. Thermoelasticity based on fractional telegraph equation. In: Fractional thermoelasticity, part of the solid mechanics and its applications. Vol. 219. Częstochowa: Springer; 2015. 10.1007/978-3-319-15335-3_7Search in Google Scholar

[73] Hajizadeh A, Shah NA, Shah SIA, Animasaun IL, Rahimi-Gorji M, Alarifi IM. Free convection flow of nanofluids between two vertical plates with damped thermal flux. J Mol Liq. 2019;289:110964. 10.1016/j.molliq.2019.110964Search in Google Scholar

[74] Liang Y, Tlili I, Farooq MU, Butt K. Magnetohydrodynamics free convection flow of Carbon nanotubes viscous nanofluids over an infinite plate with Newtonian heating and fractional derivative. Math Meth Appl Sci. 2020;6481:1–11. 10.1002/mma.6481Search in Google Scholar

[75] Ahmed N, Shah NA, Ahmad B, Shah SIA, Ulhaq S, Rahimi-Gorji M. MHD convective flow of fractional nanofluid between vertical plates. J Appl Comput Mech. 2019;5:592–602. Search in Google Scholar

[76] Sheikh NA, Ching DLC, Khan I, Sakidin HB, Jamil M, Khalid HU, et al. Fractional model for MHD flow of Casson fluid with cadmium telluride nanoparticles using the generalized Fouriers law. Sci Rep. 2021;11:16117. 10.1038/s41598-021-95528-zSearch in Google Scholar PubMed PubMed Central

[77] Asjad MI, Aleem M, Ahmadian A, Salahshour S, Ferrara M. New trends of fractional modeling and heat and mass transfer investigation of (SWCNTs and MWCNTs)-CMC based nanofluids flow over inclined plate with generalized boundary conditions. Chinese J Phys. 2020;66:497–516. 10.1016/j.cjph.2020.05.026Search in Google Scholar

[78] Khan AQ, Rasheed A. Mixed convection magnetohydrodynamics flow of a nanofluid with heat transfer: a numerical study. Math Problems Eng. 2019:8129564. 10.1155/2019/8129564Search in Google Scholar

[79] Anwar MS, Ahmad RTM, Shahzad T, Irfan M, Ashraf MZ. Electrified fractional nanofluid flow with suspended carbon nanotubes. Comput Math Appl. 2020;80:1375–86. 10.1016/j.camwa.2020.07.005Search in Google Scholar

[80] Babitha, Madhura KR, Makinde OD. Computational study on heat transfer and MHD-electrified flow of fractional Maxwell nanofluids suspended with SWCNT and MWCNT. Heat Transfer. 2021;50:5813–34. 10.1002/htj.22150Search in Google Scholar

[81] Gul T, Khan MA, Noman W, Khan I, Alkanhal TA, Tlili I. Fractional order forced convection carbon nanotube nanofluid flow passing over a thin needle. Symmetry. 2019;11:312. 10.3390/sym11030312Search in Google Scholar

[82] Gul T, Anwar H, Khan MA, Khan I, Kumam P. Integer and non-integer order study of the GO-W/GO-EG nanofluids flow by means of Marangoni convection. Symmetry. 2019;11:640. 10.3390/sym11050640Search in Google Scholar

[83] Aly AM, Raizah Z, Al-Hanaya A. Double rotations between an inner wavy shape and a hexagonal-shaped cavity suspended by NEPCM using a time-fractional derivative of the ISPH method. Int Commun Heat Mass Transf. 2021;127:105533. 10.1016/j.icheatmasstransfer.2021.105533Search in Google Scholar

[84] Al-Hanaya Roohi RA, Heydari MH, Sun HG. Numerical study of unsteady natural convection of variable-order fractional Jeffrey nanofluid over an oscillating plate in a porous medium involved with magnetic, chemical and heat absorption effects using Chebyshev cardinal functions. Eur Phys J Plus. 2019;134:535. 10.1140/epjp/i2019-12873-9Search in Google Scholar

[85] Azhar WA, Vieru D, Fetecau C. Free convection flow of some fractional nanofluids over a moving vertical plate with uniform heat flux and heat source. Phys Fluids. 2017;29:082001. 10.1063/1.4996034Search in Google Scholar

[86] Ali F, Ahmad Z, Arif M, Khan I, Nisar KS. A time fractional model of generalized couette flow of couple stress nanofluid with heat and mass transfer: applications in engine oil. IEEE Access. 2020;8:146944. 10.1109/ACCESS.2020.3013701Search in Google Scholar

[87] Abro KA, Abdon A. A computational technique for thermal analysis in coaxial cylinder of one-dimensional flow of fractional Oldroyd-B nanofluid. Int J Ambient Energy. 2022;43(1):5357–65.10.1080/01430750.2021.1939157Search in Google Scholar

[88] Aleem M, Asjad MI, Shaheen A, Khan I. MHD Influence on different water based nanofluids (TiO2, Al2O3, CuO) in porous medium with chemical reaction and newtonian heating. Chaos Solitons Fractals. 2020;130:109437. 10.1016/j.chaos.2019.109437Search in Google Scholar

[89] Abro KA, Hussain M, Baig MM. An analytic study of molybdenum disulfide nanofluids using the modern approach of Atangana-Baleanu fractional derivatives. Eur Phys J Plus. 2017;132:439. 10.1140/epjp/i2017-11689-ySearch in Google Scholar

[90] Jan SAA, Ali F, Sheikh NA, Khan I, Saqib M, Gohar M. Engine oil based generalized brinkman-type nano-liquid with molybdenum disulphide nanoparticles of spherical shape: Atangana-Baleanu fractional model. Numer Meth Partial Differ Equ. 2018;34:1472–88. 10.1002/num.22200Search in Google Scholar

[91] Saqib M, Khan I, Shafie S. Application of Atangana-Baleanu fractional derivative to MHD channel flow of CMC-based-CNTs nanofluid through a porous medium. Chaos Solitons Fractals. 2018;116:79–85. 10.1016/j.chaos.2018.09.007Search in Google Scholar

[92] Abro KA, Rashidi MM, Khan I, Abro IA, Tassaddiq A. Analysis of Stokes second problem for Nanofluids using modern approach of Atangana-Baleanu fractional derivative. J Nanofluids. 2018;7:738–47. 10.1166/jon.2018.1486Search in Google Scholar

[93] Khan I. New idea of Atangana and Baleanu fractional derivatives to human blood flow in nanofluids. Chaos. 2019;29:013121. 10.1063/1.5078738Search in Google Scholar PubMed

[94] Saqib M, Ali F, Khan I, Sheikh NA, Shafie SB. Convection in ethylene glycol-based molybdenum disulfide nanofluid. J Therm Anal Calorim. 2019;135:523–32. 10.1007/s10973-018-7054-9Search in Google Scholar

[95] Saqib M, Khan I, Shafie S. Shape effect in magnetohydrodynamic free convection flow of sodium alginate-ferrimagnetic nanofluid. J Therm Sci Eng Appl. 2019;11:041019–1. 10.1115/1.4044201Search in Google Scholar

[96] Abro KA, Laghari MH, Gomez-Aguilar JF. A aplication of Atangana-Baleanu fractional derivative to carbon nanotubes based non-Newtonian nanofluid: applications in nanotechnology. J Appl Comput Mech 2020;6:1260–9. Search in Google Scholar

[97] Ali F, Saqib M, Khan I, Sheikh NA. Heat transfer analysis in ethylene glycol based molybdenum disulfide generalized nanofluid via Atangana-Baleanu fractional derivative approach. Studies in systems, fractional derivatives with Mittag-Leffler kernel. 2019;194:217–33. 10.1007/978-3-030-11662-0_13Search in Google Scholar

[98] Tassaddiq A, Khanb I, Nisar KS. Heat transfer analysis in sodium alginate based nanofluid using MoS2 nanoparticles: Atangana-Baleanu fractional model. Chaos Solitons Fractals. 2020;130:109445. 10.1016/j.chaos.2019.109445Search in Google Scholar

[99] Arif M, Ali. F, Khan I, Nisar KS. A time fractional model with non-singular kernel the generalized Couette flow of fouple stress nanofluid. IEEE Access. 2020;8:77378–95. 10.1109/ACCESS.2020.2982028Search in Google Scholar

[100] Saqib M, Kasim ARM, Mohammad NF, Ling D, Ching C, Shafie S. Application of fractional derivative without singular and local kernel to enhanced heat transfer in CNTs manofluid over an inclined plate. Symmetry. 2020;12:768. 10.3390/sym12050768Search in Google Scholar

[101] Khan I, Saqib M, Alqahtani AM. Channel flow of fractionalized H2O-based CNTs nanofluids with Newtonian heating. Discrete Contin Dyn Syst. 2020;13:769–79. 10.3934/dcdss.2020043Search in Google Scholar

[102] Murtaza S, Iftekhar M, AliAamina F, Khan I. Exact analysis of non-Linear electro-osmotic flow of generalized Maxwell nanofluid: applications in aoncrete based nano-materials. IEEE Access. 2020;4:99. 10.1109/ACCESS.2020.2988259Search in Google Scholar

[103] Abro KA, Chandio AD, Abro IA, Khan I. Dual thermal analysis of magnetohydrodynamic flow of nanofluids via modern approaches of Caputo-Fabrizio and Atangana-Baleanu fractional derivatives embedded in porous medium. J Therm Anal Calorim. 2019;135:2197–207. 10.1007/s10973-018-7302-zSearch in Google Scholar

[104] Abro KA, Khan I, Nisar KS, Alsagri AS. Effects of carbon nanotubes on magnetohydrodynamic flow of methanol based nanofluids via Atangana-Baleanu and Caputo-Fabrizio derivatives. Therm Sci. 2019;23:883–98. 10.2298/TSCI180116165ASearch in Google Scholar

[105] Abro KA, Soomro M, Atangana A, GomezAguilar JF. Thermophysical properties of Maxwell nanofuids via fractional derivatives with regular kernel. J Therm Anal Calorim. 2022;147:449–59.10.1007/s10973-020-10287-9Search in Google Scholar

[106] Abro KA, Siyal A, Atangana A. Thermal stratifcation of rotational second grade fuid through fractional diferential operators. J Therm Anal Calorim. 2021;143:3667–76. 10.1007/s10973-020-09312-8Search in Google Scholar

[107] Ali F, Murtaza S, Sheikh NA, Khan I. Heat transfer analysis of generalized Jeffery nanofluid in a rotating frame: Atangana-Balaenu and Caputo-Fabrizio fractional models. Chaos Solitons Fractals. 2019;129:1–5. 10.1016/j.chaos.2019.08.013Search in Google Scholar

[108] Xiao Y, Shah NA, Irshad T. Magneto-hydrodynamics natural convection flows of viscous carbon nanotubes nanofluids with generalized Fourier’s law in a vertical cylinder. Math Meth Appl Sci. 2020;6566:1–6. 10.1002/mma.6566Search in Google Scholar

[109] Danish Ikram M, Imran Asjad M, Ahmadian A, Ferrara M. A new fractional mathematical model of extraction nanofluids using clay nanoparticles for different based fluids. Math Meth Appl Sci. 2020;6568:1–14. 10.1002/mma.6568Search in Google Scholar

[110] Saqib M, Khan I, Chu Y, Qushairi A, Shafie S, Nisar KS. Multiple fractional solutions for magnetic bio-nanofluid using Oldroyd-B model in a porous medium with ramped wall heating and variable velocity. Appl Sci. 2020;10:3886. 10.3390/app10113886Search in Google Scholar

[111] Elnaqeeb T, Shah NA, Mirza IA. Natural convection flows of carbon nanotubes nanofluids with Prabhakar-like thermal transport. Math Meth Appl Sci. 2020;1–14. 10.1002/mma.6584Search in Google Scholar

[112] Tanveer M, Ullah S, Shah NA, Thermal analysis of free convection fows of viscous carbon nanotubes nanofuids with generalized thermal transport: a Prabhakar fractional model. J Therm Anal Calorim. 2021;144:2327–36. 10.1007/s10973-021-10643-3Search in Google Scholar

[113] Wang F, Asjad MI, Zahid M, Iqbal A, Ahmad H, Alsulami MD. Unsteady thermal transport flow of Casson nanofluids with generalized Mittage Leffler kernel of Prabhakaras type. J Mater Res Technol. 2021;14:1292–300. 10.1016/j.jmrt.2021.07.029Search in Google Scholar

[114] Arafa AM, Rashed ZZ, Ahmed SE. Radiative fow of non Newtonian nanofuids within inclined porous enclosures with time fractional derivative. Sci Rep. 2021;11:5338. 10.1038/s41598-021-84848-9Search in Google Scholar PubMed PubMed Central

[115] Azwadi CSN, Adamu IM, Jamil MM. Preparation methods and thermal performance of hybrid nanofluids. J Adv Rev Sci Res. 2016;241:13–23. Search in Google Scholar

[116] Hossein K, Saeed A, Hootan M, Rasool K, Somchai W, Masoud A. A comprehensive review on rheological behavior of mono and hybrid nanofluids: effective parameters and predictive correlations. Int J Heat Mass Transf. 2018;127:997–1012. 10.1016/j.ijheatmasstransfer.2018.07.103Search in Google Scholar

[117] Baby TT, Ramaprabhu S. Experimental investigation of the thermal transport properties of a carbon nanohybrid dispersed nanofluid. Nanoscale. 2011;3(5):2208–14. 10.1039/c0nr01024cSearch in Google Scholar PubMed

[118] Huang D, Wu Z, Sunden B. Effects of hybrid nanofluid mixture in plate heat exchangers. Exp Thermal Fluid Sci. 2016;72:190–6. 10.1016/j.expthermflusci.2015.11.009Search in Google Scholar

[119] Hussanan A, Salleh MZ, Khan I, Shafie S. Convection heat transfer in micropolar nanofluids with oxide nanoparticles in water, kerosene and engine oil. J Mol Liq. 2017;229:482–8. 10.1016/j.molliq.2016.12.040Search in Google Scholar

[120] Aman S, Khan I, Ismail Z, Salleh MZ, Alshomrani AS, Alghamdi MS. Magnetic field effect on Poiseuille flow and heat transfer of carbon nanotubes along a vertical channel filled with Casson fluid. AIP Adv. 2017;7:015036. 10.1063/1.4975219Search in Google Scholar

[121] Bing KY, Hussanan A, Mohamed KKA, Sarif NM, Ismail Z, Salleh MZ. Thermal radiation effect on MHD flow and heat transfer of Williamson nanofluids over a stretching sheet with Newtonian heating. AIP Confer Proc. 2017;1830:020022. 10.1063/1.4980885Search in Google Scholar

[122] Fallah B, Dinarvand S, Yazdi ME, Rostami MN, Pop I. MHD flow and heat transfer of SiC-TiO2/DO hybrid nanofluid due to a permeable spinning disk by a novel algorithm. J Appl Comput Mech. 2019;5:976–88. Search in Google Scholar

[123] Reddy MG, Shehzad SA. Molybdenum disulfide and magnesium oxide nanoparticle performance on micropolar Cattaneo-Christov heat flux model. Appl Math Mech Engl Ed. 2021;42:541–52. 10.1007/s10483-021-2713-9Search in Google Scholar

[124] Tripathi1 D, Prakash J, Reddy MG, Kumar R. Numerical study of electroosmosis-induced alterations in peristalticpumping of couple stress hybrid nanofluids through microchannel. Indian J Phys. 2021;95:2411–21. 10.1007/s12648-020-01906-0Search in Google Scholar

[125] Izady M, Dinarvand S, Pop I, Chamkha AJ. Flow of aqueous Fe2O3-CuO hybrid nanofluid over a permeable stretching/shrinking wedge: a development on Falkne-Skan problem. Chinese J Phys. 2021;74:406–20. 10.1016/j.cjph.2021.10.018Search in Google Scholar

[126] Mousavi SM, Rostami MN, Yousefi M, Dinarvand S, Pop I, Sheremet MA. Dual solutions for Casson hybrid nanofluid flow due to a stretching/shrinking sheet: A new combination of theoretical and experimental models. Chinese J Phys. 2021;71:574–88. 10.1016/j.cjph.2021.04.004Search in Google Scholar

[127] Jabbaripour B, Nademi Rostami M, Dinarvand S, Pop I. Aqueous aluminium-copper hybrid nanofluid flow past a sinusoidal cylinder considering three-dimensional magnetic field and slip boundary condition. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering. 10.1177/09544089211046434. Search in Google Scholar

[128] Safw N, Norihan K, Arifin M, Pop I. Magnetohydrodynamics (MHD) boundary layer flow of hybrid nanofluid over a moving plate with Joule heating. Alexandria Eng J. 2022;61:1938–45. 10.1016/j.aej.2021.07.032Search in Google Scholar

[129] Alsaedi A, Muhammad K, Hayat T. Numerical study of MHD hybrid nanofluid flow between two coaxial cylinders. Alexandr Eng J. 2022;61:8355–62. 10.1016/j.aej.2022.01.067Search in Google Scholar

[130] Berrehal H, Dinarvand S, Khan I. Mass-based hybrid nanofluid model for entropy generation analysis of flow upon a convectively-warmed moving wedge. Chinese J Phys. 2022;77:2603–16. 10.1016/j.cjph.2022.04.017Search in Google Scholar

[131] Dinarvand S. Nodal/saddle stagnation-point boundary layer flow of CuOCAg/water hybrid nanofluid: a novel hybridity model. Microsyst Technol. 2019;25:2609–23. 10.1007/s00542-019-04332-3Search in Google Scholar

[132] Aman S, Zokriderivative SM, Ismail Z, Salleh MZ, Khan I. Effect of MHD and porosity on exact solutions and flow of a Hybrid Casson-nanofluid. J Adv Res Fluid Mech Therm Sci. 2018;44:131–9. Search in Google Scholar

[133] Aman S, Zokri SM, Ismail Z, Salleh MZ, Khan I. Casson model of MHD flow of SA–Based hybrid nanofluid using Caputo time-fractional models. Defect Diffusion Forum Online. 2019;390:83–90. 10.4028/www.scientific.net/DDF.390.83Search in Google Scholar

[134] Ahmed SE. Caputo fractional convective flow in an inclined wavy vented cavity filled with a porous medium using Al2O3-Cu hybrid nanofluids. Int Commun Heat Mass Transf. 2020;116:104090. 10.1016/j.icheatmasstransfer.2020.104690Search in Google Scholar

[135] Ali R, Asjad MI, Akgul A. An analysis of a mathematical fractional model of hybrid viscous nanofluids and its application in heat and mass transfer. J Comput Appl Math. 2021;383:113096. 10.1016/j.cam.2020.113096Search in Google Scholar

[136] Ali R, Asjad MI, Aldalbahi A, Gorji MR, Rahaman M. Convective fow of a Maxwell hybrid nanofuid due to pressure gradient in a channel. J Therm Anal Calorim. 2021;143:1319–29. 10.1007/s10973-020-10304-xSearch in Google Scholar

[137] Ali R, Akgul A, Asjad MI. Power law memory of natural convection flow of hybrid nanofluids with constant proportional Caputo fractional derivative due to pressure gradient. Pramana-J Phys. 2020;94:131. 10.1007/s12043-020-01997-8Search in Google Scholar

[138] DanishIkram M, Asjad MI, Akgul A, Baleanu D. Effects of hybrid nanofluid on novel fractional model of heat transfer flow between two parallel plates. Alexandria Eng J. 2021;60:3593–604. 10.1016/j.aej.2021.01.054Search in Google Scholar

[139] Chu Y, Ikram MD, Asjad MI, Ahmadian A, Ghaemi F. Infuence of hybrid nanofuids and heat generation on coupled heat and mass transfer fow of a viscous fuid with novel fractional derivative. J Therm Anal Calorim. 2021;144:2057–77. 10.1007/s10973-021-10692-8Search in Google Scholar

[140] Gohar M, Ali F, Khan I, Sheikh NA, Shah A. The unsteady flow of generalized hybrid nanofluids: applications in cementitious materials. J Australian Ceramic Soc. 2019;55:657–66. 10.1007/s41779-018-0275-3Search in Google Scholar

[141] Ahmad M, Imran MA, Nazar M. Mathematical modeling of (Cu-Al2O3)water based Maxwell hybrid nanofluids with Caputo-Fabrizio fractional. Adv Mech Eng. 2020;12(9):1–11. 10.1177/1687814020958841Search in Google Scholar

[142] Saqib M, Khan I, Shafie S. Application of fractional differential equations to heat transfer in hybrid nanofluid: modeling and solution via integral transforms. Adv Differ Equ. 2019;2019:52. 10.1186/s13662-019-1988-5Search in Google Scholar

[143] Saqib M, Shafie S, Khan I, Chu Y, Nisar KS. Symmetric MHD channel flow of nonlocal fractional model of BTF containing hybrid nanoparticles. Symmetry. 2020;12:663. 10.3390/sym12040663Search in Google Scholar

[144] Anwar T, Kumam P, Thounthong P. A comparative fractional study to evaluate thermalperformance of NaAlg-MoS2-Co hybrid nanofluid subject to shape factor and dual ramped conditions. Alexandria Eng J. 2022;61(3):2166–87.10.1016/j.aej.2021.06.085Search in Google Scholar

[145] Anwar T, Kumam P, Thounthong P. Fractional modeling and exact solutions to analyze thermal performance of Fe3O4-MoS2-Water hybrid nanofluid flow over an inclined surface with ramped heating and ramped boundary motion. IEEE Access. 2021;9:12389. 10.1109/ACCESS.2021.3051740Search in Google Scholar

[146] Ye X, Kandlikar SG, Li C. Viscosity of nanofluids containing anisotropic particles: a critical review and a comprehensive model. Eur Phys J E. 2019;42:159. 10.1140/epje/i2019-11923-7Search in Google Scholar PubMed

[147] Otanicar TP, Phelan PE, Prasher RS, Rosengarten G, Taylor RA. Nanofluid based direct absorption solar collector. J Renewable Sustainable Energy. 2010;2:033102. 10.1063/1.3429737Search in Google Scholar

[148] Loganathan P, Nirmal Chand P, Ganesan P. Radiation effects on an unsteady natural convective flow of a nanofluid past an infinite vertical plate. Nano Br Rep Rev. 2013;8:1–10. 10.1142/S179329201350001XSearch in Google Scholar

[149] Bait O, Ameur MS. Enhanced heat and mass transfer in solar stills using nanofluids: a review. Solar Energy. 2018;170:694–722. 10.1016/j.solener.2018.06.020Search in Google Scholar

[150] Aman S, Khan I, Ismail Z, Salleh MZ, Tlili I. A new Caputo time fractional model for heat transfer enhancement of water based graphene nanofluid: an application to solar energy. Results Phys. 2018;9:1352–62. 10.1016/j.rinp.2018.04.007Search in Google Scholar

[151] Abro KA, Memon AA, Abro SH, Khan I, Tlili I. Enhancement of heat transfer rate of solar energy via rotating Jeffrey nanofluids using Caputo-Fabrizio fractional operator: an application to solar energy. Energy Reports. 2019;5:41–49. 10.1016/j.egyr.2018.09.009Search in Google Scholar

[152] Sheikh NA, Ali F, Khan I, Gohar M, Saqib M. On the applications of nanofluids to enhance the performance of solar collectors: A comparative analysis of Atangana-Baleanu and Caputo-Fabrizio fractional models. Eur Phys J Plus. 2017;132:540. 10.1140/epjp/i2017-11809-9Search in Google Scholar

[153] Sheikha NA, Ali F, Khand I, Gohar M. A theoretical study on the performance of a solar collector using CeO2 and Al2O3 water based nanofluids with inclined plate: Atangana-Baleanu fractional model. Chaos Solitons Fractals 2018;115:135–42. 10.1016/j.chaos.2018.08.020Search in Google Scholar

[154] Aamina, Ali F, Khan I, Sheikh NA, Gohar M. Exact solutions for the Atangana-Baleanu time-fractional model of a Brinkman-type nanofluid in a rotating frame: applications in solar collectors. Eur Phys J Plus. 2019;134:119. 10.1140/epjp/i2019-12455-ySearch in Google Scholar

[155] ElBialy E, Shalaby M. An experimental investigation of a v-corrugated absorber single basin solar still using PCM. Desalination. 2016;398:147–255. 10.1016/j.desal.2016.07.042Search in Google Scholar

[156] Panchal H, Sadasivuni KK, Suresh M, Yadav S. Performance analysis of evacuated tubes coupled solar still with double basin solar still and solid fins. Int J Ambient Energy. 2022;41(9):1031–7. 10.1080/01430750.2018.1501745Search in Google Scholar

[157] Elbar ARA, Hassan H. An experimental work on the performance of solar still incorporating with wind turbine and thermal energy storage unit, Desalin Water Treat. 2019;165:24–34. 10.5004/dwt.2019.24492Search in Google Scholar

[158] Elango T, Kannan A, Murugavel KK, Performance study on single basin single slope solar still with different water nanofluids. Desalination. 2015;360:45–51. 10.1016/j.desal.2015.01.004Search in Google Scholar

[159] Sharshir SW, Peng G, Wu L, Yang N, Essa FA, Elsheikh AH, et al. Enhancing the solar still performance using nanofluids and glass cover cooling: experimental study. Appl Therm Eng. 2017;113:684–93. 10.1016/j.applthermaleng.2016.11.085Search in Google Scholar

[160] Rashidi S, Akar S, Bovand M, Ellahi R. Volume of fluid model to simulate the nanofluid flow and entropy generation in a single slope. Solar Still. 2018;115:400–10. 10.1016/j.renene.2017.08.059Search in Google Scholar

[161] El-Gazar Hamdy Hassan EF, Rabia SI, Zahra WK. Fractional modeling for enhancing the thermal performance of conventional solar still using hybrid nanofluid: Energy and exergy analysis. Eur Phys J Plus. 2021;136:717. 10.1140/epjp/s13360-021-01654-ySearch in Google Scholar

[162] Khan AK, Rashid R, Murtaza G, Zahra A. Gold nanoparticles: synthesis and applications in drug delivery. Tropical J Pharm Res. 2014;13:1169–77. 10.4314/tjpr.v13i7.23Search in Google Scholar

[163] Eldabe NT, Moatimid GM, El-Shekhipy AA, Aballah NF. Peristaltic blood flow with gold nanoparticles on a Carreau nanofluid through a non-Darcian porous medium. J Biomaterials Nanobiotechnol. 2018;9:0487707. 10.4236/jbnb.2018.94019Search in Google Scholar

[164] Mekheimer KS, Hasona WM, Abo-Elkhair RE, Zaher AZ. Peristaltic blood flow with gold nanoparticles as a third grade nanofluid in catheter: application of cancer therapy. Phys Lett A. 2018;382:85–93. 10.1016/j.physleta.2017.10.042Search in Google Scholar

[165] Abdelsalam SI, Mekheimer KS, Zaher AZ. Alterations in blood stream by electroosmotic forces of hybrid nanofluid through diseased artery: Aneurysmal/stenosed segment. Chinese J Phys. 2020;67:314–29. 10.1016/j.cjph.2020.07.011Search in Google Scholar

[166] Al-Habahbeh OM, Al-Saqqa M, Safi M, Khater TA. Review of magneto hydrodynamic pump applications. Alexandria Eng J. 2016;55(2):1347–58. 10.1016/j.aej.2016.03.001Search in Google Scholar

[167] Cao L, Zhang P, Si X. Electroosmotic fow of two-layer fuid containing Oldroyd-B fuid with fractional derivative in a rotating microparallel channel. Microfluidics Nanofluidics. 2022;26:34. 10.1007/s10404-022-02539-xSearch in Google Scholar

[168] Liang P, Wang S, Zhao M. Numerical study of rotating electroosmotic flow of Oldroyd-B fluid in a microchannel with slip boundary condition. Chinese J Phys. 2020;65:459–71. 10.1016/j.cjph.2020.02.025Search in Google Scholar

[169] Abd Elmaboud Y. Electroosmotic flow of generalized Burgers’ fluid with Caputo–Fabrizio derivatives through a vertical annulus with heat transfer. Alex Eng J. 2020;59:4563–75. 10.1016/j.aej.2020.08.012Search in Google Scholar

[170] Alsharif AM, Abdellateef AI, Elmaboud YA, Abdelsalam SI. Performance enhancement of a DC-operated micropump with electroosmosis in a hybrid nanofluid: fractional Cattaneo heat flux problem. Appl Math Mech -Engl Ed. 2022;43:931–44. 10.1007/s10483-022-2854-6Search in Google Scholar

[171] Alsharif AM, Abd Elmaboud Y. Electroosmotic flow of generalized fractional second grade fluid with fractional Cattaneo model through a vertical annulus. Chinese J Phys. 2022;77:1015–28. 10.1016/j.cjph.2021.08.021Search in Google Scholar

Received: 2022-07-07

Revised: 2022-08-11

Accepted: 2022-09-14

Published Online: 2022-12-13

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/ntrev-2022-0496

Keywords for this article

nanofluid; fractional derivatives; Buongiorno model; Tiwari and Das model

Creative Commons

BY 4.0