Abstract
This work aims to advance the room-temperature manipulation of photonic qubits and enhance coherence preservation in and for quantum applications via tailored spatio-spectral localized (SSL) systems. We focus on an innovative all-plasmonic SSL system consisting of a gold bowtie array on a gold substrate. This design produces a high-Q spectral-localized mode through the lattice array, emerging from the collective lattice response of localized surface plasmon resonance (LSPR), particularly the surface lattice resonance (SLR). The SSL system enables tunable modal coupling between the LSPR and SLR, allowing precise alignment with quantum emitters to form quasi-bound states across an energy range of 1.45–1.91 eV. This flexibility allows us to investigate how innovative configurations – such as three-body coupling symmetry and modal-coupling strength – affect coherence protection. These insights pave the way for optimizing SSL systems, setting the stage for significant advancements in nanophotonic qubit manipulation at ambient conditions and the future of photonic quantum systems.
1 Introduction
Coherence time is a critical parameter in quantum technologies, influencing the precision and effectiveness of qubit manipulation [1], [2]. Traditional quantum computing systems utilizing dielectric photonic cavity designs [3], [4], [5], [6] following principles of cavity quantum electrodynamics (cQED) typically operate at cryogenic temperatures to achieve sufficient coupling strength for effectively “capturing” qubits, a process that can be both energetically costly and inefficient. In contrast, plasmonic nanoantennas and nanocavities facilitate quantum manipulation at ambient conditions [7], [8], [9], [10], [11], leveraging their resonant modes with significantly reduced mode volumes and enhanced intensities. These concentrated mode fields create “hotspots” where a high local-density-of-states (LDOS) can effectively “capture” quantum emitters (QEs) and promote the formation of plexcitons for manipulation [11], [12]. However, the benefits of nanoplasmonic spatial localization are partly offset by intrinsic metallic losses, which can lead to decoherence, primarily due to dissipation [13], [14], [15].
Recently, the concept of quantum nanoplasmonic coherent perfect absorption (qnCPA) [16] has been introduced. Leveraging an inherent frequency specificity to selectively initialize a coupled system in a chosen plasmon-emitter dressed state, it has been demonstrated that qnCPA allows (through a coherent, unidirectional, and non-perturbing near-field energy transfer from a proximal plasmonic waveguide) to render a plexciton state robust against dynamic dissipation under ambient conditions [16].
An alternative strategy for enhancing coherence in cQED systems is to hybridize plasmonic nanoantennas with dielectric microcavities, creating “optoplasmonic” systems [14], [17]. Examples include plasmonic nanoparticles hybridized with polystyrene beads [18], plasmonic nanorods coupled with whispering-gallery-mode microcavities [19], and long-range surface plasmons interacting with waveguide modes [20]. These systems utilize high-quality (high-Q) photonic modes for spectral localization, acting as capacitors to protect coherence [20], [21], [22], [23]. Notably, atom-photon quasi-bound states (qBS) in plasmonic-dielectric hybrids [24] can suppress decoherence through unique eigenstates that exhibit low decay rates, similar to the Friedrich–Wintgen quasi-bound states in the continuum (quasi-BIC) found in photonic systems [25]. This suppression of decoherence is crucial for enhancing quantum system performance by prolonging coherence times. However, implementing these hybrid designs presents significant experimental challenges, particularly in achieving qBS under specific coupling conditions. For instance, in structures like gold nanorod dimers on nanobeams [26], precise alignment is essential: the dimer must be accurately centered within the photonic taper, and the QE must be positioned exactly at the center of the dimer. This meticulous positioning requires advanced techniques [27], [28]. One potential solution is integrating all components on a chip [29], [30], though this approach still faces challenges in achieving precise overlay accuracy across multiple materials.
These challenges can be effectively addressed through plasmonic lattice designs [31], [32], [33], which enable one-stop fabrication in a single material platform. This approach eliminates the need for precise repositioning or complex integration, allowing QEs to be spin-coated onto the surface for collective signal measurement. Importantly, lattice arrays can support high-Q surface lattice resonance (SLR) modes
Here, we introduce the concept of a spatio-spectral localized (SSL) system, where modes are considered localized only if their spatial or spectral confinement matches the size or bandwidth of the QE. This concept highlights the system’s potential for quantum manipulation under ambient conditions and demonstrates the generation of a quasi-bound state (qBS) through QE-SSL hybridization. In particular, we present and discuss an experimentally accessible plasmonic metasurface platform that achieves SSL via LSPR-SLR modal coupling, allowing easy tailoring to align with specific QEs. To analyze this SSL system quantitatively, we develop a comprehensive modal-coupling model that extracts modal-coupling parameters from electric field measurements. These modal parameters are applied in a generalized three-body quantum model, where a practical QE, e.g., excitons in monolayer MoS2, interacts with the SSL system. The resulting spectral intensity and dynamics illustrate how LSPR spatially captures the QE while SLR spectrally stores quantum coherence, effectively forming a qBS. Beyond the exemplified LSPR-SLR modal coupling, we explore coupling symmetry breaking and variations in coupling strength to provide general insights into QE-SSL hybridization and quantum coherence protection. It should be noted that this work focuses exclusively on dissipation while neglecting other decoherence effects such as dephasing and depolarization. Overall, our goal is to generalize the concept of SSL modal coupling for broader applications in plasmonic cQED systems.
2 Theory and concept
To score in an imaginary game of basketball, one strategy would be to align the ball with a stationary net, while an alternative approach would involve moving the net to accommodate the (oncoming) ball, as illustrated in Figure 1(a). Using this analogy, the quantum emitter (QE) – which may be a quantum dot, nitrogen-vacancy (NV) center, or exciton in 2D materials – represents the fixed ball, as its material properties often constrain its positioning due to the complexities of synthesis and fabrication. Conversely, tuning the cavity system is more feasible, as its modes and couplings can be designed and engineered using readily available materials and established fabrication techniques. This tunable cavity system acts as the adjustable net, designed to hybridize effectively with the fixed QE.
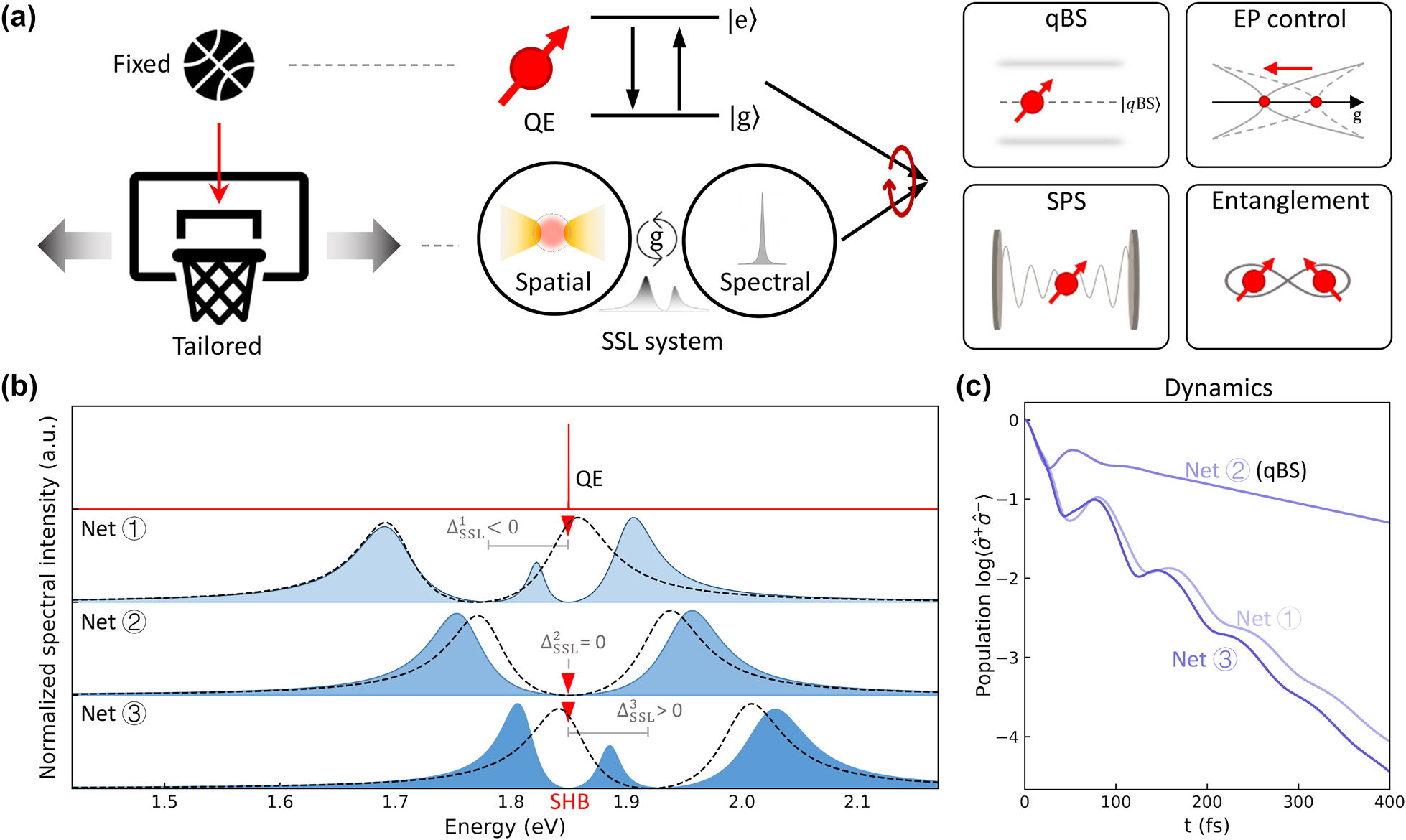
Spatio-spectral localized (SSL) modal coupling for atom-photon quasi-bound states (qBS) (a) schematic of the matching process involving a fixed quantum emitter (QE) modeled as a two-level system and an SSL system with a broad spatial-localized mode and a narrow spectral-localized mode, enabling various quantum applications. (b) Three different SSL systems with strong modal coupling (dashed lines), exhibiting spectral splitting, are tuned around a QE oscillating at ω e = 1.85 eV, represented by tailored nets 1, 2, and 3. The QE (red triangles) induces spectral hole-burning (SHB) in the SSL-QE hybrid systems (blue-shaded). (c) Dynamics of the QE in the three tailored SSL systems in (b). The Net 2, identified as a qBS, allows the longest coherence lifetime of the QE.
Our approach involves developing an SSL system, acting as a tailored net. This concept is exemplified by optoplasmonic systems that combine plasmonic antennas with photonic cavities. In these systems, a spatial-localized mode offered by plasmonic antennas is engineered to concentrate the electromagnetic field within a small mode volume, which enhances coupling with the QE, effectively “capturing” the ball. Concurrently, a spectral-localized mode (e.g., photonic cavities) with a high Q-factor can be designed to preserve coherence and extend the lifetime of the QE.
Indeed, such a QE-SSL hybridization is crucial for quantum applications involving QEs. For example, (i) Quasi-bound State (qBS) [24]: An exotic eigenstate in the QE-SSL system that protects the quantum coherence of the QE. (ii) Exceptional Point (EP) Control [38]: Spatio-spectral couplings are adjusted to reach the EP, enhancing interaction between the QE and the spatial-localized mode. (iii) Single Photon Source (SPS) [39]: The SSL system spatially captures the QE, enhancing emission rates with the spatial-localized mode, while the spectral-localized mode maintains the indistinguishability and purity of emitted photons. (iv) Entanglement [8]: Strong coupling among QEs occurs under ambient conditions, with spatial-localized modes amplifying QE oscillations and spectral-localized modes preserving coherence, thereby enhancing overall concurrence.
2.1 QE-SSL hybridization
The QE-SSL hybridization can be theoretically captured on the basis of a cQED framework, where an SSL system exhibits spatio-spectral modal coupling, described by a generalized three-body quantum model. Here, we consider a simplified system and model with one spatial-localized mode α and one spectral-localized mode β, characterized by resonant frequencies ω
α
and ω
β
, and decay rates γ
α
and γ
β
respectively, with the assumption that γ
α
≫ γ
β
. The QE is modeled as a two-level system with a transition dipole moment μ
e aligned with the local electric field and a transition frequency ω
e. Its intrinsic decay rate is calculated as
The system is described in the Fock state representation, with a full Hamiltonian under the rotating-wave approximation, which is expressed as:
including the free Hamiltonian:
the interaction Hamiltonian:
and the driving Hamiltonian:
where ω denotes the probing frequency. The operators
We calculate the steady-state density matrix ρ(ω) at the probing frequency ω, and the spectral intensity for α, β, and the QE is given by:
2.2 Quasi-bound-state in a QE-SSL system
The time evolution of the QE-SSL system is described based on a master equation:
where the dynamics of the density matrix ρ is governed by coherent evolution under the Hamiltonian H and losses associated with the modes α, β, and the QE. These losses are described by Lindblad terms in the standard form:
The respective equations of motion can be expressed as:
These equations indicate the effective non-Hermitian Hamiltonian in the single-excitation subspace, which can be expressed as follows:
This Hamiltonian possesses three eigenvalues, one of which is purely real when the QE-SSL detuning is given by:
The corresponding eigenstate acts as a “bound state” that protects the quantum coherence of the QE. Although achieving ideal protection with zero loss is challenging due to intrinsic decay rates γ
e, γ
α
and γ
β
, this eigenstate still results in the slowest decay of the QE, thus being referred to as qBS [24]. Under a special condition of g
eβ
= 0, the qBS is positioned at
3 Designing a full-plasmonic SSL system
Integrating and aligning plasmonic antennas with photonic cavities in optoplasmonic systems can be challenging. We propose using high-Q surface lattice resonances (SLR) within an array architecture as the spectral localization component, as shown in Figure 2. This method simplifies integration with plasmonic nanoantennas, creating an all-plasmonic platform. Introducing a QE from monolayer MoS2 into this platform can lead to the formation of the qBS. The system allows for straightforward tuning to optimize the interaction with the QE. In this scenario, we assume that the spatial-localized mode α and the QE are resonantly driven by a weak pump, such that Ω α = Ωe ∼ 0.1γ e.
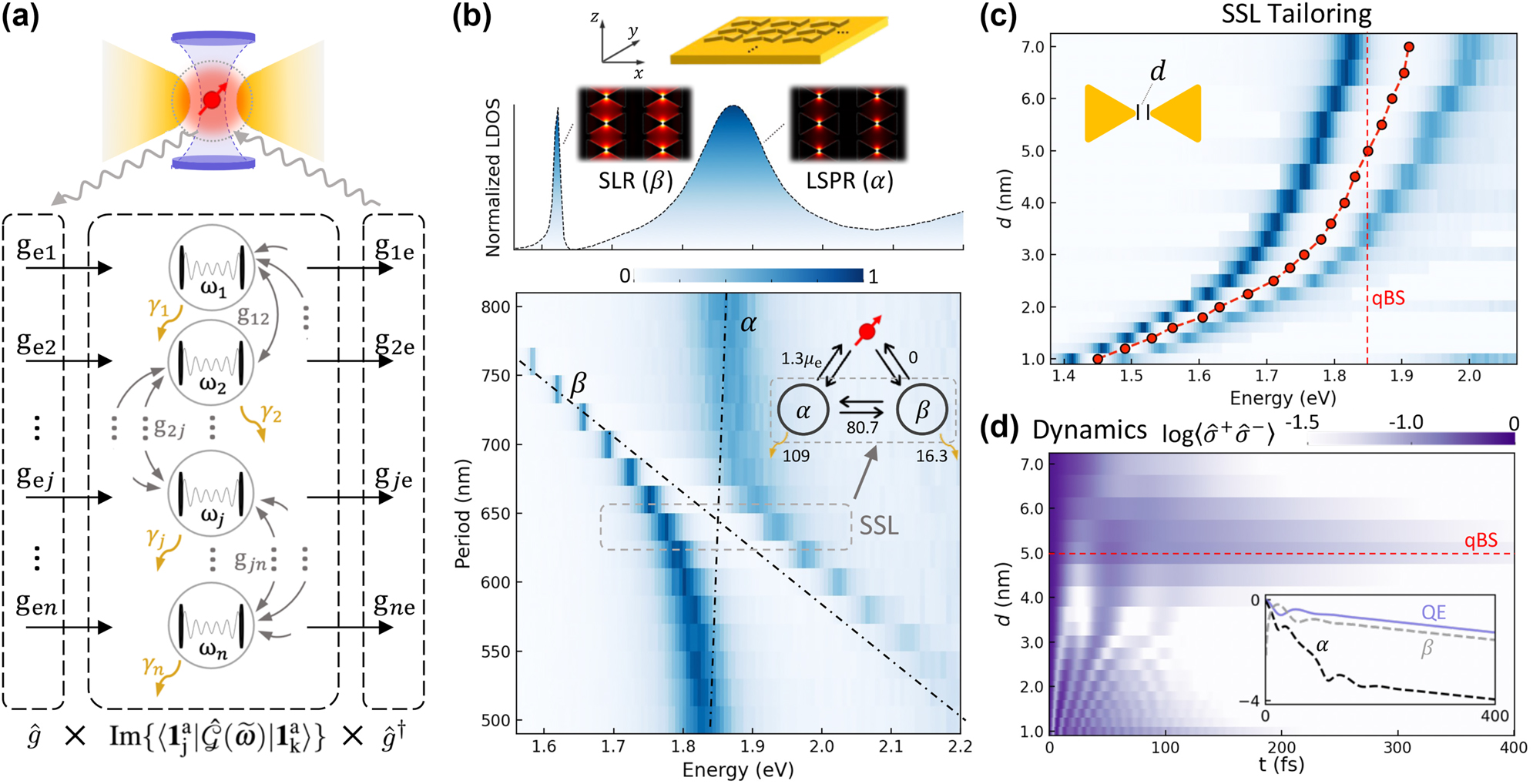
Designing a full-plasmonic tunable SSL system. (a) Quantum modal-coupling model for extracting coupling rates from the response field intensity under a point dipole source excitation. (b) Plasmonic bowtie-array metasurface showcasing localized surface plasmon resonance (LSPR) mode (α, spatially localized mode, ω α = 1.87 eV, γ α = 117 meV) and surface lattice resonance (SLR) mode (β, spectrally localized mode, ω β = 1.62 eV, γ β = 10.6 meV) before modal coupling. The calculated normalized local-density-of-states (LDOS) at the position of the dipole source displays an anti-crossing feature as the lattice period along the x-axis varies from 500 to 800 nm, with observed spectral splitting at the crossing point (ω α = ω β ) indicating a zero-detuned SSL system (extracted g αβ = 80.7 meV) with strong modal coupling. (c) Tailoring zero-detuned SSL systems: the splitting spectrum is tuned as d increases from 1.0 to 7.0 nm, corresponding to tunable ω SSL (red dots) from 1.45 to 1.91 eV (650–855 nm). (d) For a fixed QE with ω e = 1.85 eV and μ e = 46 D throughout this study, we can select an SSL system from the map (c) to achieve the qBS at d = 5 nm with ΔSSL = ω SSL − ω e = 0 when the dynamics of QE is traced. At the qBS, full dynamics of α, β, and the QE are shown in the inset on a logarithmic scale.
3.1 Modal-coupling model
Modal coupling between two modes – one spatially localized with a broad band and the other spectrally localized with a narrow band – typically results in Fano line shapes [52], which depend on the modes’ properties and their coupling. To evaluate system performance in the quantum regime and differentiate near-field coupling from far-field interference, we previously developed a model that analyzes Fano line shapes from scattering by extracting parameters like coupling and decay rates (radiative and non-radiative) [51], rather than relying on shape parameters [53]. This approach provides a more physically grounded description and enables analysis of coupling across multiple modes. In this work, we extend this by developing a modal-coupling model to analyze Fano line shapes generated by fields excited from a point source.
In a modal-coupling system, the point source is modeled as a dipole placed at r e, where the field generated by the point dipole simultaneously drives the dipole, as described by Fermi’s golden rule:
Here,
Equation (9) acts as a bridge connecting the classical and quantum frameworks, i.e., the total transition probabilities from a quantum perspective correspond to the spectral density over the continuous spectrum from the classical viewpoint, which can be computed using the Green’s function of the field [47] (see Supplementary Information S1 for detailed derivation).
In the quantum framework, transitions occur among photon states, moving from point source states to the states of the modal-coupling system and back to the point states, as illustrated in Figure 2(a). The modal-coupling system comprises n quasinormal modes (QNMs), where the jth (j = 1, 2, …, n) mode is defined as
The states
The vector
By combining Eqs. (9)–(12), we derive the LDOS relationship (see Supplementary Information S2 for details):
This relationship takes the same form as those reported in previous works [54]. To extract g ej , g jk , ω j and γ j , we fit the quantum framework described in Eq. (13) to the classical results of LDOS, which are typically calculated through numerical simulations. The extracted mode properties and coupling parameters will serve as inputs for our three-body quantum model described in Sections 2.1 and 2.2. In the subsequent section, this fitting process will be illustrated in the context of designing a plasmonic bowtie-array metasurface.
3.2 Numerical designing of plasmonic bowtie-array metasurfaces
As shown in Figure 2(b), our SSL system features a gold bowtie array on a gold substrate, creating a plasmonic metasurface. The bowties are arranged in an orthogonal array along the directions of x and y. This system exhibits two key modes. The spatial-localized mode α, corresponding to the localized surface plasmon resonance (LSPR), features a concentrated field at the gap’s center and oscillates in-plane along the x direction. The spectral-localized mode β, associated with surface lattice resonances (SLRs), results from the collective response of the LSPRs and is uniformly distributed over the surface [34], [35]. Under continuous excitation, the modes α and β coexist with the QE positioned at the center of the bowtie gap (see Supplementary Information Figure S1), enabling potential coupling among all three. We model this interaction using our generalized modal-coupling approach, which allows us to derive the coupling properties without making assumptions.
For any given bowtie geometry (e.g., d = 5.0 nm), we can adjust the array period along the x direction to achieve zero detuning between LSPR and SLR. To do so, we excite the structure with an electric dipole source (dipole moment aligned along the x direction) at the gap center on the surface and measure the normalized LDOS spectrum from the bowtie array. As shown in Figure 2(b), the LDOS spectra exhibit anti-crossing behavior as the period changes from 500 to 800 nm. This results in an SSL system at the crossing point, where ω SSL = ω α = ω β .
To conduct a quantitative analysis, we apply our modal-coupling model to extract coupling parameters by establishing the transition matrix for the α − β modal-coupling system according to Eq. (11). The LDOS spectrum is then calculated from the response electric field (see details in Supplementary Information S3), yielding the expression:
This equation enables us to fit the frequencies ω
α
and ω
β
, decay rates γ
α
and γ
β
, and coupling rates g
αβ
, g
eα
, and g
eβ
to the response electric field
We analyze the excited LDOS for an LSPR-SLR metasurface with a large period of 740 nm, revealing distinct linear spectra for the α (LSPR) and β (SLR) modes, which do not couple (i.e., the superposition of Lorentzian shapes calculated with ω α = 1.87 eV, ω β = 1.62 eV, γ α = 117 meV, and γ β = 10.6 meV), as shown in Figure 2(b), top. As the period decreases, ω α remains relatively stable, while ω β shows significant variation, which can be fitted with linear trends [32], [36], [37]. At the crossing point for the resonant metasurface shown in Figure 2(b), bottom, we fit the data under the constraint ω α ≈ ω β . We find ω α = 1.86 eV and ω β = 1.85 eV, with a small detuning of 0.01 eV due to discrete period selection at 20 nm intervals. This deviation is acceptable for the SSL system, allowing us to assume ω α = ω β in discussions where Δ αβ ≤ 0.01 eV. The modal-coupling rate is found to be g αβ = 80.7 meV, confirming strong modal coupling since g αβ > (γ α − γ β )/4 [47]. The coupling rate to the QE shows g eα = 1.3μ e, consistent with previous findings [47]. Notably, the fitting indicates no coupling between the QE and β (see Supplementary Information S4). This may be explained by the SLR mechanism, where collective oscillations in the bowtie array overshadow any influence from the QE, which lacks sufficient strength to affect its neighbors [36]. In contrast, the LSPR acts as an antenna, amplifying the QE’s oscillation and facilitating interaction with neighboring bowties.
Next, we can repeat this process (numerical simulation and fitting) by varying the bowtie geometry, specifically the inter-gap distance d, see Figure 2(c), to ensure that our SSL system frequency ω SSL resonates with the fixed QE for reaching the qBS condition in Eq. (8). We observe an increase in ω SSL from 1.45 eV to 1.91 eV as d varies from 1.0 nm to 7.0 nm.
We then input the extracted key parameters, ω
α(β), γ
α(β), g
eα
, g
eβ
, and g
αβ
, into the master equation Eq. (5) of the three-body quantum model to study the dynamics. As an example, for a fixed QE with ω
e = 1.85 eV and μ
e = 46 D, the dynamics of the QE in the QE-SSL systems as a function of distance d are shown in Figure 2(d). The selected configuration shows the longest coherence lifetime under conditions for forming the qBS (
In summary, we have developed a plasmonic bowtie-array metasurface that aligns with our objective of creating a simple, tunable SSL system, easily adaptable for constructing the desired QE-SSL systems. We have exemplified the qBS, which will be further explored in the next section to examine its properties in relation to the diversified scenarios of the QE-SSL hybridization.
4 Quantum coherence protection
To shed light on the intriguing dynamics of QE-SSL hybridization and the protection of quantum coherence, we explore the effects of various excitation pathways, the implications of breaking QE-SSL coupling symmetry, and the role of modal-coupling strength in this section. By examining these factors, we aim to uncover how they influence the interplay between the QE and the SSL system, enriching our understanding of their collaborative potential.
4.1 Effect of excitation pathways
Different excitation conditions in experiments can affect the quantum coherence protection at the qBS. This section will compare various excitation pathways for the exemplified plasmonic bowtie metasurface SSL system, as illustrated in Figure 3. In the three-body quantum model described in Sections 2.1 and 2.2, the driving Hamiltonian interacts with different components – the QE, α, or β – serving as the excitation source to determine the steady-state spectral densities and establishes the initial excitation states of all components at the onset of the dynamics. The driving is assumed to be weakly coherent pumping, as described in Section 3.1 (Ω α or Ωe ∼ 0.1γ e) under the jump-free approximation [24], [56]. Note that Ω β = 0 is set, as we assume β cannot be directly excited by an external source. For dynamics calculations, these weak pumps are insufficient to represent the dissipation trajectory. Instead, we initialize the system to its starting states using an ideal ultrafast pump pulse with negligible duration before the dynamics begin. Thus, the light sources discussed in this section, whether a laser or a halogen lamp [7], [41], are assumed to serve as a weak continuous pump for spectral intensity calculations and as an ideal ultrafast pump pulse to initialize the starting states for the dynamics calculation. They determine the different excitation pathways in the following three cases.
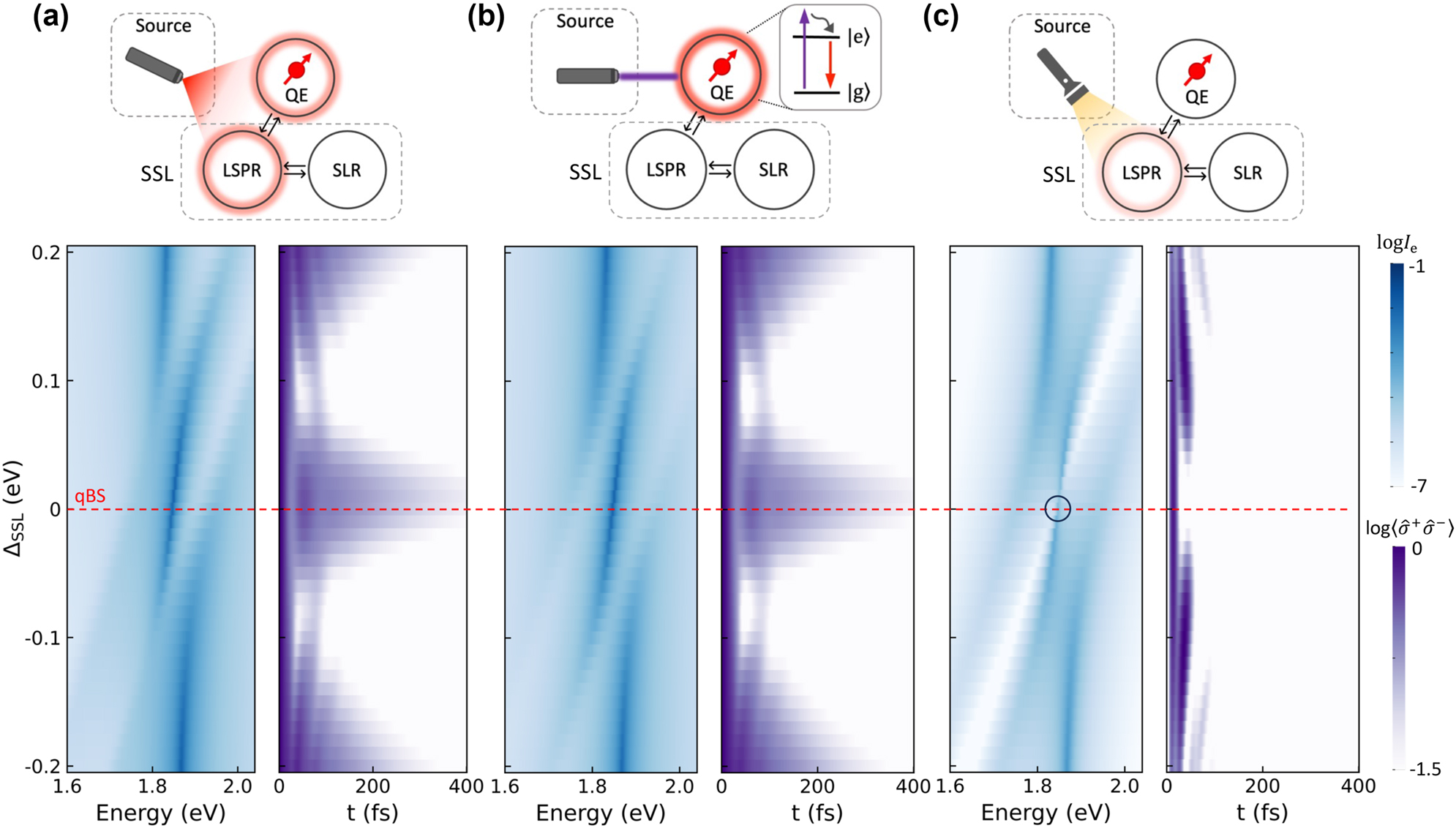
The effect of excitation pathways on quantum coherence protection. The dependence of the QE’s spectral intensity (blue) and dynamics (purple) on the pumping configurations: (a) resonant laser pumping to excite both QE and LSPR. (b) Higher-frequency laser pumping to excite the QE alone. (c) Ambient white-light pumping to excite the LSPR alone. Here, the QE is fixed with ω e = 1.85 eV throughout this study, and the SSL systems are tuned with ΔSSL = ω SSL − ω e.
The first case (Figure 3(a)) represents “resonant excitation” [57], [58] , i.e., the default case throughout this study, where a laser with energy matching the QE irradiates the SSL-QE system. The broad linewidth of the α LSPR mode allows for simultaneous excitation with the QE, while the β SLR mode is not expected to be directly excited due to its formation mechanism. Dynamic calculations are performed with both α and the QE initially in their excited states, while β is in its ground state, as illustrated in the Inset dynamics of Figure 2(d). Now we assume the SSL system can be tuned freely, with ΔSSL varying from −0.2 to 0.2 eV. The spectral intensity and dynamics of the QE are represented in two color maps using gradient shades of blue and purple. The spectral intensity reveals three deep blue arms, showing two anti-crossings at ΔSSL = −0.08 and 0.08 eV, where the QE interacts with the left and right peaks of the SSL splitting (see Figure 1(b)). These arms indicate regions where the QE’s spectral intensity remains unaffected by the SSL system, correlating with prolonged quantum coherence time in the dynamic plot. Coherence time increases with greater detuning in the upper and lower regions, as the SSL system’s spectral range moves away from the QE. Conversely, coherence time decreases near the qBS at zero detuning, highlighted by a red dashed line, which marks the longest coherence time across the dynamic map. The anti-crossings in the spectral intensity map are symmetrically positioned around the qBS, and the dynamic map also displays a symmetric distribution centered at the qBS, establishing this QE-SSL system as symmetric with respect to detuning from the qBS.
The second case (Figure 3(b)) addresses “higher-frequency excitation”, where the laser frequency significantly exceeds the QE’s resonant frequency to avoid simultaneous excitation of the LSPR. In practical scenarios, the QE is not a pure two-level system: it often includes higher non-radiative states [59], [60], [61]. These higher states can be reached first, followed by non-radiative relaxation to the excited state |e⟩, allowing the QE to function as an initially excited two-level system within the SSL-QE framework. In this setting, the spectral intensity and dynamic maps show little variation from the first case in Figure 3(a), suggesting that simultaneous excitation of the LSPR does not significantly affect the QE’s performance in the QE-SSL system.
The third case (Figure 3(c)) explores an extraordinary method of driving the QE-SSL system using “ambient light” from conventional white light sources, such as halogen lamps [7], [41], commonly used in scattering measurements. These sources are spatially diffuse and spectrally broadband, which makes direct excitation of the QE challenging but effectively stimulates the LSPR [62], leveraging spatially localized modes with high decay rates across a broad spectrum. This results in distinct changes: the spectral intensity at the three arms decreases, and the prolonged coherence time seen in previous cases vanishes. Specifically, The qBS line (ΔSSL = 0) intersects a white ribbon representing the SSL splitting valley, creating a vanishing point (highlighted by a black circle in Figure 3(c)) on the middle blue arm. This point corresponds to the shortest dynamics in the purple map. Here, symmetric dynamics in the upper and lower regions are shortened, indicating that the SSL system drives the QE through its SSL splitting peaks, accelerating decoherence. Notably, qBS cannot be achieved unless the QE is initially excited, highlighting the behavior of a dark state that is difficult to access through coupling pathways.
Despite these changes, symmetry about ΔSSL = 0 in all maps is preserved, suggesting that this characteristic arises from the internal mechanisms of the QE-SSL system rather than the specific excitation pathways.
4.2 Breaking QE-SSL coupling symmetry
In previous case studies of plasmonic bowtie-array metasurfaces coupled to in-plane excitons in monolayer MoS2, the QE was only coupled to α – the spatial-localized LSPR mode as predicted by our modal-coupling model. However, the QE may also couple to the spectral-localized β mode in other QE-SSL systems. This section will differentiate between the two coupling scenarios, as shown in Figure 4.
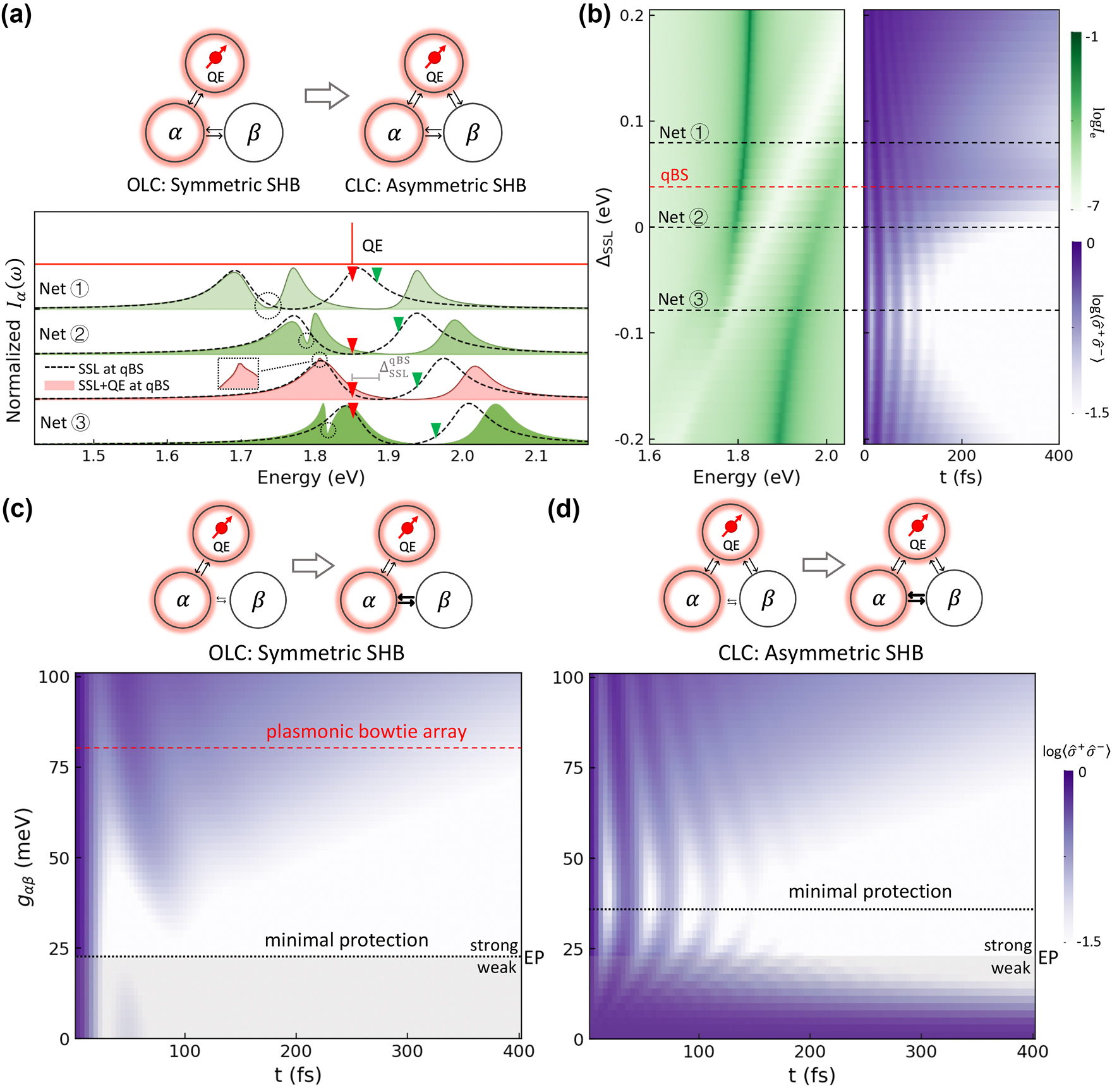
From open-loop coupling (OLC) symmetric to closed-loop coupling (CLC) asymmetric QE-SSL systems. (a) The same three SSL systems in Figure 1(b) (dashed lines), exhibiting SSL splitting, are tuned around a QE oscillating at ω e = 1.85 eV. The QE (red triangles) induces asymmetric SHB features in the SSL-QE hybrid systems 1–3 (green-shaded) and a qBS hybrid system (pink-shaded) when g eβ = g eα around right SSL peak (green triangles) and left SSL peak (circles). (b) For a fixed QE with ω e = 1.85 eV and μ e = 46 D throughout this study, we can design an SSL system to achieve the qBS according to Eq. (8). The dependence of spectral intensity (green) and dynamics (purple) on ΔSSL, where the four hybrid systems from (a) are labeled. (c) and (d) The dependence of dynamics on the modal-coupling strength g αβ of α and β at qBS under different coupling conditions: (c) OLC g eβ = 0 and (d) CLC g eβ = g eα .
As illustrated in Figure 4(a), we now assume g eβ = g eα , leading to closed-loop coupling (CLC) where all coupling links are established within the three-body quantum system. We present two additional scenarios in the Supplementary Information S5: g eβ < g eα and g eβ > g eα . In contrast, the earlier system with g eβ = 0 features open-loop coupling (OLC). First, we present the SHB characteristics of the CLC, which is shown in green or pink in Figure 4(a). Unlike the OLC SHB in Figure 1(b), which displays symmetric spectral holes on the left and right SSL peaks as detuning varies, the CLC SHB demonstrates asymmetry. The asymmetry is evident when comparing the transitions from SSL splitting (dashed lines) to the QE-SSL (green-shaded) and qBS hybrid system (pink-shaded) spectra. The hole burnings by the QE (red triangles) are more pronounced on the right SSL peak, causing significant shifts and alterations in that region (green triangles). The SHB further splits the right SSL peak into left and right components, with the left component interacting with the left SSL peak, resulting in Fano line shapes, as indicated by the circles. This asymmetry aligns with findings from our previous work, where a microcavity mode created asymmetric holes in a plexcitonic system [22]. More excitingly, the qBS system exhibits a sharp tip atop the left SSL peak (Inset) instead of destructive line shapes. This occurs when the Fano asymmetry parameter q → ∞ [63], indicating the formation of a quasi-bound state in the continuum (quasi-BIC) within photonic structures [64].
The QE’s spectral intensity and dynamic maps for the asymmetric CLC are presented in Figure 4(b), revealing asymmetric characteristics, in contrast to Figure 3. In the spectral intensity map, the three color arms are reduced to two, with the upper arm covering a larger area and appearing stronger than the lower arm. The dynamic map retains three regions, but the middle region shifts upward. As predicted by Eq. (8), the qBS occurs ΔSSL = 0.036 eV for g eβ = g eα , marked by the red dashed line, aligning very well with the dynamic simulation result. Thus, a non-zero g eβ establishes CLC among α, β, and the QE, resulting in symmetry breaking of SHB, spectral intensity, and dynamics, along with a shift in the qBS. Since the qBS remains robust even when symmetry is broken, asymmetric QE-SSL systems can be designed to protect coherence in situations where the symmetric coupling is challenging [21], [22].
4.3 Effect of modal-coupling strength
One interesting feature of our all-plasmonic resonant SSL is that it functions in a strong modal coupling regime where g αβ > (γ α − γ β )/4. We are interested in exploring the implications of the resonant SSL system operating outside this regime by comparing the coherence protection capability of the qBS against variations in g αβ from 1 meV (weak modal coupling) to 100 meV (strong modal coupling), with the boundary at g αβ = 23.2 meV. This comparison encompasses both the symmetric OLC system and the asymmetric CLC system. We highlight g αβ = 80.7 meV, derived from our case study of plasmonic bowtie-array metasurface SSL system (d = 5.0 nm), in both cases using red dashed lines.
In the symmetric OLC system in Figure 4(c), the coherence time of the qBS decreases as g
αβ
increases in the weak modal coupling regime but begins to improve in the strong modal coupling regime. This behavior is due to β acting as an additional loss in weak modal coupling and as a capacitor for coherence storage in strong modal coupling by an indirect pathway connecting with the QE through
In the asymmetric CLC system shown in Figure 4(d), the qBS behavior varies significantly with g
αβ
. Compared to the OLC system, the CLC system exhibits more oscillations during qBS decay, although both show similar trends as g
αβ
increases. The qBS achieves optimal protection in the weak modal coupling regime at g
αβ
= 0, where the direct storage pathway
In summary, modal-coupling strength significantly affects qBS protection performance. In both symmetric and asymmetric systems, higher g αβ enhances protection, with the asymmetric system offering better protection in the weak modal coupling regime. However, further increases in g αβ may lead to improved qBS, indicating a positive outlook for developing stronger modal coupling in SSL systems.
5 Conclusions and outlook
This work highlights the potential of spatio-spectral localized (SSL) systems to enhance qubit manipulation and preserve coherence in quantum applications. By demonstrating the formation of a quasi-bound state (qBS) within a QE-SSL system, we gained insight related to the nature and relative importance of the interactions between a QE, a spatially localized mode, and a spectrally localized mode. For this, we developed a modal-coupling model that extracts the relevant quantum parameters from our design of a fully plasmonic tunable SSL system, i.e., plasmonic bowtie-array metasurface. This design enables precise alignment with a fixed QE at the qBS, enhancing coherence protection while reducing fabrication challenges. It can be easily tuned across an energy range of 1.45–1.91 eV by adjusting the period and gap thickness. Additionally, the design facilitates the straightforward integration of QEs from 2D materials, as these can be directly assembled onto the bowtie array [65]. The gold substrate elevates the localized surface plasmon resonance (LSPR) field at the bowtie tips, effectively capturing the QEs [66], [67]. Compared to optoplasmonic SSL systems, our plasmonic bowtie-array metasurface offers a simpler, more robust design with a single-layer fabrication process and potentially deterministic plexcitonic coupling at the single-emitter level. This is achieved by precisely positioning the emitter at the electromagnetic hotspot for optimal field enhancement and aligning its dipole moment with the mode polarization, ensuring consistent performance. Its seamless integration with 2D materials makes the system practical and scalable.
We also explored how the excitation pathway affects the performance of the QE-SSL system, emphasizing the importance of external excitation for forming a qBS. Our examination of the coupling symmetry between the QE and SSL, as well as the effects of modal-coupling strength, showed that the system’s SHB symmetry breaks when moving from open-loop to closed-loop coupling. Importantly, we found that stronger modal coupling enhances the protection of the qBS.
Further enhancing our understanding of QE-SSL interactions will enable exploring novel coupling strategies to optimize SSL system performance. Future research should focus on improving qubit coherence times and operational fidelity and assessing environmental impacts on SSL performance as well as experimental validation of our models and refinement of fabrication techniques. While our study demonstrates the interaction between a single QE and a single SSL system, the theory can be easily expanded to include multiple QEs and SSL systems by adjusting matrix dimensions. This expansion could lead to significant applications in plasmonic circuits. The ongoing exploration of SSL systems and their integration with quantum emitters will contribute to advancing robust quantum technologies, benefiting quantum computing, communication, and sensing.
Funding source: Science Foundation Ireland
Award Identifier / Grant number: 18/RP/6236
Funding source: Natural Science Foundation of Henan Province
Award Identifier / Grant number: 232300421141
Funding source: Guangdong Provincial Department of Science and Technology
Award Identifier / Grant number: GDZX2406001
Funding source: Singapore University of Technology and Design
Award Identifier / Grant number: SKI 2021-02-14
Award Identifier / Grant number: SKI 2021-04-12
Award Identifier / Grant number: SRG SMT 2021 169
Funding source: National Research Foundation Singapore
Award Identifier / Grant number: NRF-CRP26-2021-0004
Award Identifier / Grant number: NRF2021-QEP2-02-P03
Award Identifier / Grant number: NRF2021-QEP2-03-P09
Funding source: National Natural Science Foundation of China
Award Identifier / Grant number: 11874438
Award Identifier / Grant number: 12374326
-
Research funding: This work was supported by the National Research Foundation Singapore (Grants NRF2021-QEP2-02-P03, NRF2021-QEP2-03-P09, NRF-CRP26-2021-0004), the Ministry of Education Singapore (Grant MOE-T2EP50223-0001), and the Singapore University of Technology and Design (Start-Up Research Grant SRG SMT 2021 169 and Kickstarter Initiatives SKI 2021-02-14, SKI 2021-04-12). WJZ acknowledges the support of the Ph.D. RSS. YWL acknowledges the support from Guangdong Provincial Quantum Science Strategic Initiative via Grant No. GDZX2406001. JFL acknowledges the support from the National Natural Science Foundation of China via Grant No. 11874438. RML acknowledges the support from the National Natural Science Foundation of China via Grant No. 12374326 and the Key Project of Natural Science Foundation of Henan via Grant No. 232300421141. OH gratefully acknowledges funding from Research Ireland (formally: Science Foundation Ireland) via Grant No. 18/RP/6236.
-
Author contributions: WJZ, OH, and LW conceptualized the project. OH and LW provided supervision throughout the project. WJZ, YWL, and JFL developed the theoretical model. WJZ performed the numerical simulations. RL and LKA contributed to the investigation methodology and the creation of the visualizations. WJZ, JFL, OH, and LW drafted the manuscript. All authors contributed to data analysis and critically reviewed the manuscript. All authors have accepted responsibility for the entire content of this manuscript and consented to its submission to the journal, reviewed all the results and approved the final version of the manuscript.
-
Conflict of interest: Authors state no conflict of interest.
-
Informed consent: Informed consent was obtained from all individuals included in this study.
-
Data availability: The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
[1] S. Putz, et al.., “Protecting a spin ensemble against decoherence in the strong-coupling regime of cavity qed,” Nat. Phys., vol. 10, no. 10, pp. 720–724, 2014. https://doi.org/10.1038/nphys3050.Search in Google Scholar
[2] M. Steffen, M. Sandberg, and S. Srinivasan, “Recent research trends for high coherence quantum circuits,” Supercond. Sci. Technol., vol. 30, no. 030301, pp. 10–1088, 2017. https://doi.org/10.1088/1361-6668/aa55a2.Search in Google Scholar
[3] H. Zheng, D. J. Gauthier, and H. U. Baranger, “Waveguide-QED-based photonic quantum computation,” Phys. Rev. Lett., vol. 111, no. 9, 2013, Art. no. 090502. https://doi.org/10.1103/physrevlett.111.090502.Search in Google Scholar PubMed
[4] A. W. Elshaari, W. Pernice, K. Srinivasan, O. Benson, and V. Zwiller, “Hybrid integrated quantum photonic circuits,” Nat. Photonics, vol. 14, no. 5, pp. 285–298, 2020. https://doi.org/10.1038/s41566-020-0609-x.Search in Google Scholar PubMed PubMed Central
[5] A. Kavokin, T. C. H. Liew, C. Schneider, P. G. Lagoudakis, S. Klembt, and S. Hoefling, “Polariton condensates for classical and quantum computing,” Nat. Rev. Phys., vol. 4, no. 7, pp. 435–451, 2022. https://doi.org/10.1038/s42254-022-00447-1.Search in Google Scholar
[6] M. J. Weaver, et al.., “An integrated microwave-to-optics interface for scalable quantum computing,” Nat. Nanotechnol., vol. 19, no. 2, pp. 166–172, 2024. https://doi.org/10.1038/s41565-023-01515-y.Search in Google Scholar PubMed
[7] R. Chikkaraddy, et al.., “Single-molecule strong coupling at room temperature in plasmonic nanocavities,” Nature, vol. 535, no. 7610, pp. 127–130, 2016. https://doi.org/10.1038/nature17974.Search in Google Scholar PubMed PubMed Central
[8] M. Hensen, T. Heilpern, S. K. Gray, and W. Pfeiffer, “Strong coupling and entanglement of quantum emitters embedded in a nanoantenna-enhanced plasmonic cavity,” ACS Photonics, vol. 5, no. 1, pp. 240–248, 2018. https://doi.org/10.1021/acsphotonics.7b00717.Search in Google Scholar
[9] H. Groß, J. M. Hamm, T. Tufarelli, O. Hess, and B. Hecht, “Near-field strong coupling of single quantum dots,” Sci. Adv., vol. 4, no. 3, 2018, Art. no. eaar4906. https://doi.org/10.1126/sciadv.aar4906.Search in Google Scholar PubMed PubMed Central
[10] X. Xiao, J.-B. You, P. Bai, C. Eng Png, Z.-K. Zhou, and L. Wu, “Ultrastrong coupling in single plexcitonic nanocubes,” Nanophotonics, vol. 9, no. 2, pp. 257–266, 2020. https://doi.org/10.1515/nanoph-2019-0333.Search in Google Scholar
[11] X. Xiong, N. Kongsuwan, Y. Lai, C. E. Png, L. Wu, and O. Hess, “Room-temperature plexcitonic strong coupling: ultrafast dynamics for quantum applications,” Appl. Phys. Lett., vol. 118, no. 13, 2021. https://doi.org/10.1063/5.0032013.Search in Google Scholar
[12] A. Manjavacas, F. J. G. de Abajo, and P. Nordlander, “Quantum plexcitonics: strongly interacting plasmons and excitons,” Nano Lett., vol. 11, no. 6, pp. 2318–2323, 2011. https://doi.org/10.1021/nl200579f.Search in Google Scholar PubMed
[13] G. Di Martino, et al.., “Quantum statistics of surface plasmon polaritons in metallic stripe waveguides,” Nano Lett., vol. 12, no. 5, pp. 2504–2508, 2012. https://doi.org/10.1021/nl300671w.Search in Google Scholar PubMed
[14] S. V. Boriskina, et al.., “Losses in plasmonics: from mitigating energy dissipation to embracing loss-enabled functionalities,” Adv. Opt. Photonics, vol. 9, no. 4, pp. 775–827, 2017. https://doi.org/10.1364/aop.9.000775.Search in Google Scholar
[15] S. G. Dlamini, et al.., “Probing decoherence in plasmonic waveguides in the quantum regime,” Phys. Rev. Appl., vol. 9, no. 2, 2018, Art. no. 024003. https://doi.org/10.1103/physrevapplied.9.024003.Search in Google Scholar
[16] Y. Lai, et al.., “Room-temperature quantum nanoplasmonic coherent perfect absorption,” Nat. Commun., vol. 15, no. 1, p. 6324, 2024. https://doi.org/10.1038/s41467-024-50574-9.Search in Google Scholar PubMed PubMed Central
[17] Da Xu, et al.., “Quantum plasmonics: new opportunity in fundamental and applied photonics,” Adv. Opt. Photonics, vol. 10, no. 4, pp. 703–756, 2018. https://doi.org/10.1364/aop.10.000703.Search in Google Scholar
[18] W. Ahn, Y. Hong, S. V. Boriskina, and B. M. Reinhard, “Demonstration of efficient on-chip photon transfer in self-assembled optoplasmonic networks,” ACS Nano, vol. 7, no. 5, pp. 4470–4478, 2013. https://doi.org/10.1021/nn401062b.Search in Google Scholar PubMed
[19] Y. Chen, Y. Yin, L. Ma, and O. G. Schmidt, “Recent progress on optoplasmonic whispering-gallery-mode microcavities,” Adv. Opt. Mater., vol. 9, no. 12, 2021, Art. no. 2100143. https://doi.org/10.1002/adom.202100143.Search in Google Scholar
[20] K. Chevrier, J.-M. Benoit, C. Symonds, J. Paparone, J. Laverdant, and J. Bellessa, “Organic exciton in strong coupling with long-range surface plasmons and waveguided modes,” ACS Photonics, vol. 5, no. 1, pp. 80–84, 2018. https://doi.org/10.1021/acsphotonics.7b00556.Search in Google Scholar
[21] P. Peng, et al.., “Enhancing coherent light-matter interactions through microcavity-engineered plasmonic resonances,” Phys. Rev. Lett., vol. 119, no. 23, 2017, Art. no. 233901. https://doi.org/10.1103/physrevlett.119.233901.Search in Google Scholar
[22] W.-J. Zhou, et al.., “Cavity spectral-hole-burning to boost coherence in plasmon-emitter strong coupling systems,” Nanotechnology, vol. 33, no. 47, 2022, Art. no. 475001. https://doi.org/10.1088/1361-6528/ac8aa3.Search in Google Scholar PubMed
[23] N. Engheta, “Circuits with light at nanoscales: optical nanocircuits inspired by metamaterials,” science, vol. 317, no. 5845, pp. 1698–1702, 2007. https://doi.org/10.1126/science.1133268.Search in Google Scholar PubMed
[24] Y.-W. Lu, et al.., “Unveiling atom-photon quasi-bound states in hybrid plasmonic-photonic cavity,” Nanophotonics, vol. 11, no. 14, pp. 3307–3317, 2022. https://doi.org/10.1515/nanoph-2022-0162.Search in Google Scholar PubMed PubMed Central
[25] C. Wei Hsu, B. Zhen, A. D. Stone, J. D. Joannopoulos, and M. Soljačić, “Bound states in the continuum,” Nat. Rev. Mater., vol. 1, no. 9, pp. 1–13, 2016. https://doi.org/10.1038/natrevmats.2016.48.Search in Google Scholar
[26] M. Kamandar Dezfouli, R. Gordon, and S. Hughes, “Modal theory of modified spontaneous emission of a quantum emitter in a hybrid plasmonic photonic-crystal cavity system,” Phys. Rev. A, vol. 95, no. 1, 2017, Art. no. 013846. https://doi.org/10.1103/physreva.95.013846.Search in Google Scholar
[27] S. I. Bogdanov, et al.., “Deterministic integration of single nitrogen-vacancy centers into nanopatch antennas,” arXiv preprint arXiv:1902.05996, 2019.Search in Google Scholar
[28] R. Liu, et al.., “Deterministic positioning and alignment of a single-molecule exciton in plasmonic nanodimer for strong coupling,” Nat. Commun., vol. 15, no. 1, p. 4103, 2024. https://doi.org/10.1038/s41467-024-46831-6.Search in Google Scholar PubMed PubMed Central
[29] D. Englund, et al.., “Deterministic coupling of a single nitrogen vacancy center to a photonic crystal cavity,” Nano Lett., vol. 10, no. 10, pp. 3922–3926, 2010. https://doi.org/10.1021/nl101662v.Search in Google Scholar PubMed
[30] S. Chakravarthi, et al.., “Hybrid integration of gap photonic crystal cavities with silicon-vacancy centers in diamond by stamp-transfer,” Nano Lett., vol. 23, no. 9, pp. 3708–3715, 2023. https://doi.org/10.1021/acs.nanolett.2c04890.Search in Google Scholar PubMed
[31] V. G. Kravets, A. V. Kabashin, W. L. Barnes, and A. N. Grigorenko, “Plasmonic surface lattice resonances: a review of properties and applications,” Chem. Rev., vol. 118, no. 12, pp. 5912–5951, 2018. https://doi.org/10.1021/acs.chemrev.8b00243.Search in Google Scholar PubMed PubMed Central
[32] A. I. Vakevainen, et al.., “Plasmonic surface lattice resonances at the strong coupling regime,” Nano Lett., vol. 14, no. 4, pp. 1721–1727, 2014. https://doi.org/10.1021/nl4035219.Search in Google Scholar PubMed
[33] S. R. K. Rodriguez, J. Feist, M. A. Verschuuren, F. J. G. Vidal, and J. G. Rivas, “Thermalization and cooling of plasmon-exciton polaritons: towards quantum condensation,” Phys. Rev. Lett., vol. 111, no. 16, 2013, Art. no. 166802. https://doi.org/10.1103/physrevlett.111.166802.Search in Google Scholar
[34] O. Reshef, et al.., “Multiresonant high-Q plasmonic metasurfaces,” Nano Lett., vol. 19, no. 9, pp. 6429–6434, 2019. https://doi.org/10.1021/acs.nanolett.9b02638.Search in Google Scholar PubMed
[35] M. Saad Bin-Alam, et al.., “Ultra-high-Q resonances in plasmonic metasurfaces,” Nat. Commun., vol. 12, no. 1, p. 974, 2021. https://doi.org/10.1038/s41467-021-21196-2.Search in Google Scholar PubMed PubMed Central
[36] M. J. Huttunen, K. Dolgaleva, P. Törmä, and R. W. Boyd, “Ultra-strong polarization dependence of surface lattice resonances with out-of-plane plasmon oscillations,” Opt. Express, vol. 24, no. 25, pp. 28279–28289, 2016. https://doi.org/10.1364/oe.24.028279.Search in Google Scholar
[37] Q.-Y. Lin, et al.., “Strong coupling between plasmonic gap modes and photonic lattice modes in DNA-assembled gold nanocube arrays,” Nano Lett., vol. 15, no. 7, pp. 4699–4703, 2015. https://doi.org/10.1021/acs.nanolett.5b01548.Search in Google Scholar PubMed
[38] W. Li, et al.., “Highly efficient single-exciton strong coupling with plasmons by lowering critical interaction strength at an exceptional point,” Phys. Rev. Lett., vol. 130, no. 14, 2023, Art. no. 143601. https://doi.org/10.1103/physrevlett.130.143601.Search in Google Scholar PubMed
[39] A. M. Boyce, et al.., “Plasmonic diamond membranes for ultrafast silicon vacancy emission,” Nano Lett., vol. 24, no. 12, pp. 3575–3580, 2024. https://doi.org/10.1021/acs.nanolett.3c04002.Search in Google Scholar PubMed PubMed Central
[40] S. Ahmad, et al.., “Generalized scaling law for exciton binding energy in two-dimensional materials,” Phys. Rev. Appl., vol. 13, no. 6, 2020, Art. no. 064062. https://doi.org/10.1103/physrevapplied.13.064062.Search in Google Scholar
[41] L. Yang, et al.., “Strong light–matter interactions between gap plasmons and two-dimensional excitons under ambient conditions in a deterministic way,” Nano Lett., vol. 22, no. 6, pp. 2177–2186, 2022. https://doi.org/10.1021/acs.nanolett.1c03282.Search in Google Scholar PubMed
[42] J. Klein, et al.., “Engineering the luminescence and generation of individual defect emitters in atomically thin MoS2,” ACS Photonics, vol. 8, no. 2, pp. 669–677, 2021. https://doi.org/10.1021/acsphotonics.0c01907.Search in Google Scholar
[43] R. P. Puchert, F. J. Hofmann, H. S. Angerer, J. Vogelsang, S. Bange, and J. M. Lupton, “Linearly polarized electroluminescence from mos2 monolayers deposited on metal nanoparticles: toward tunable room-temperature single-photon sources,” Small, vol. 17, no. 5, 2021, Art. no. 2006425. https://doi.org/10.1002/smll.202006425.Search in Google Scholar PubMed
[44] R. Sáez-Blázquez, Á. Cuartero-González, J. Feist, F. J. García-Vidal, and A. I. Fernández-Domínguez, “Plexcitonic quantum light emission from nanoparticle-on-mirror cavities,” Nano Lett., vol. 22, no. 6, pp. 2365–2373, 2022. https://doi.org/10.1021/acs.nanolett.1c04872.Search in Google Scholar PubMed PubMed Central
[45] J.-B. You, et al.., “Suppressing decoherence in quantum plasmonic systems by the spectral-hole-burning effect,” Phys. Rev. A, vol. 103, no. 5, 2021, Art. no. 053517. https://doi.org/10.1103/physreva.103.053517.Search in Google Scholar
[46] I. Aharonovich, D. Englund, and M. Toth, “Solid-state single-photon emitters,” Nat. Photonics, vol. 10, no. 10, pp. 631–641, 2016. https://doi.org/10.1038/nphoton.2016.186.Search in Google Scholar
[47] W. Zhou, J. Liu, J. Zhu, D. Gromyko, C. Qiu, and L. Wu, “Exceptional points unveiling quantum limit of fluorescence rates in non-hermitian plexcitonic single-photon sources,” APL Quantum, vol. 1, no. 1, 2024. https://doi.org/10.1063/5.0191494.Search in Google Scholar
[48] K. Santhosh, O. Bitton, L. Chuntonov, and G. Haran, “Vacuum Rabi splitting in a plasmonic cavity at the single quantum emitter limit,” Nat. Commun., vol. 7, no. 1, pp. 1–5, 2016. https://doi.org/10.1038/ncomms11823.Search in Google Scholar PubMed PubMed Central
[49] G. Zengin, M. Wersäll, S. Nilsson, T. J. Antosiewicz, M. Käll, and T. Shegai, “Realizing strong light-matter interactions between single-nanoparticle plasmons and molecular excitons at ambient conditions,” Phys. Rev. Lett., vol. 114, no. 15, 2015, Art. no. 157401. https://doi.org/10.1103/physrevlett.114.157401.Search in Google Scholar PubMed
[50] S. Putz, et al.., “Spectral hole burning and its application in microwave photonics,” Nat. Photonics, vol. 11, no. 1, pp. 36–39, 2017. https://doi.org/10.1038/nphoton.2016.225.Search in Google Scholar
[51] W.-J. Zhou, et al.., “Probing spectral-hole-burning in non-hermitian scatterings: differentiating far-field interference and near-field coupling,” ACS Photonics, vol. 11, no. 11, pp. 4671–4681, 2024. https://doi.org/10.1021/acsphotonics.4c01085.Search in Google Scholar
[52] S. Bay, P. Lambropoulos, and K. Mølmer, “Superradiance in a structured radiation reservoir,” Phys. Rev. A, vol. 57, no. 4, p. 3065, 1998. https://doi.org/10.1103/physreva.57.3065.Search in Google Scholar
[53] B. Gallinet and O. J. F. Martin, “Influence of electromagnetic interactions on the line shape of plasmonic fano resonances,” ACS Nano, vol. 5, no. 11, pp. 8999–9008, 2011. https://doi.org/10.1021/nn203173r.Search in Google Scholar PubMed
[54] I. Medina, F. J. García-Vidal, A. I. Fernández-Domínguez, and J. Feist, “Few-mode field quantization of arbitrary electromagnetic spectral densities,” Phys. Rev. Lett., vol. 126, no. 9, 2021, Art. no. 093601. https://doi.org/10.1103/physrevlett.126.093601.Search in Google Scholar PubMed
[55] C. Cohen-Tannoudji, J. Dupont-Roc, and G. Grynberg, Atom-Photon Interactions: Basic Processes and Applications, Hoboken, NJ, John Wiley & Sons, 1998.10.1002/9783527617197Search in Google Scholar
[56] R. J. Brecha, P. R. Rice, and M. Xiao, “N two-level atoms in a driven optical cavity: quantum dynamics of forward photon scattering for weak incident fields,” Phys. Rev. A, vol. 59, no. 3, p. 2392, 1999. https://doi.org/10.1103/physreva.59.2392.Search in Google Scholar
[57] P. Anger, P. Bharadwaj, and L. Novotny, “Enhancement and quenching of single-molecule fluorescence,” Phys. Rev. Lett., vol. 96, no. 11, 2006, Art. no. 113002. https://doi.org/10.1103/physrevlett.96.113002.Search in Google Scholar
[58] D. Li, et al.., “Plasmonic photonic crystals induced two-order fluorescence enhancement of blue perovskite nanocrystals and its application for high-performance flexible ultraviolet photodetectors,” Adv. Funct. Mater., vol. 28, no. 41, 2018, Art. no. 1804429. https://doi.org/10.1002/adfm.201804429.Search in Google Scholar
[59] S. Mouri, Y. Miyauchi, and K. Matsuda, “Tunable photoluminescence of monolayer mos2 via chemical doping,” Nano Lett., vol. 13, no. 12, pp. 5944–5948, 2013. https://doi.org/10.1021/nl403036h.Search in Google Scholar PubMed
[60] W.-T. Hsu, et al.., “Evidence of indirect gap in monolayer WSe2,” Nat. Commun., vol. 8, no. 1, p. 929, 2017. https://doi.org/10.1038/s41467-017-01012-6.Search in Google Scholar PubMed PubMed Central
[61] J. Jadczak, J. Kutrowska-Girzycka, P. Kapuściński, Y. S. Huang, A. Wójs, and L. Bryja, “Probing of free and localized excitons and trions in atomically thin WSe2, WS2, MoSe2 and MoS2 in photoluminescence and reflectivity experiments,” Nanotechnology, vol. 28, no. 39, 2017, Art. no. 395702. https://doi.org/10.1088/1361-6528/aa87d0.Search in Google Scholar PubMed
[62] Y. Niu, H. Xu, and H. Wei, “Unified scattering and photoluminescence spectra for strong plasmon-exciton coupling,” Phys. Rev. Lett., vol. 128, no. 16, 2022, Art. no. 167402. https://doi.org/10.1103/physrevlett.128.167402.Search in Google Scholar PubMed
[63] M. F. Limonov, M. V. Rybin, A. N. Poddubny, and Y. S. Kivshar, “Fano resonances in photonics,” Nat. Photonics, vol. 11, no. 9, pp. 543–554, 2017. https://doi.org/10.1038/nphoton.2017.142.Search in Google Scholar
[64] A. A. Bogdanov, et al.., “Bound states in the continuum and fano resonances in the strong mode coupling regime,” Adv. Photonics, vol. 1, no. 1, p. 016001, 2019. https://doi.org/10.1117/1.ap.1.1.016001.Search in Google Scholar
[65] H. Cai, et al.., “Charge-depletion-enhanced WSe2 quantum emitters on gold nanogap arrays with near-unity quantum efficiency,” Nat. Photonics, vol. 18, pp. 842–847, 2024. https://doi.org/10.1038/s41566-024-01460-9.Search in Google Scholar
[66] X. Xiong, et al.., “Substrate engineering of plasmonic nanocavity antenna modes,” Opt. Express, vol. 31, no. 2, pp. 2345–2358, 2023. https://doi.org/10.1364/oe.476521.Search in Google Scholar PubMed
[67] X. Xiong, et al.., “Control of plexcitonic strong coupling via substrate-mediated hotspot nanoengineering,” Adv. Opt. Mater., vol. 10, no. 17, 2022, Art. no. 2200557. https://doi.org/10.1002/adom.202200557.Search in Google Scholar
Supplementary Material
This article contains supplementary material (https://doi.org/10.1515/nanoph-2024-0574).
© 2025 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Frontmatter
- Research Articles
- Optical control of levitated nanoparticles via dipole–dipole interaction
- Spatio-spectral localized modal coupling for room-temperature quantum coherence protection
- Recovery of topologically robust merging bound states in the continuum in photonic structures with broken symmetry
- Localization of nanoscale objects with light singularities
- High accuracy inverse design of reconfigurable metasurfaces with transmission-reflection-integrated achromatic functionalities
- Fiber-assisted nanoparticle tracking analysis meets nanorheology: a novel approach for probing viscoelastic properties at the nanoscale
- Chiral phase-imaging meta-sensors
- Stimulator-multiplexing framework of microwave-infrared compatible reconfigurable metasurface integrated with LED array
- Optical phased array receiver with mode diversity and coherent combination
- BioMeta: modular reprogrammable metasurface for noninvasive human respiration monitoring
- Effectively suppressed reflected photonic spin Hall effect
- Letters
- Second harmonic generation of optical spin−orbit interactions in hybrid plasmonic nanocircuits
- One million quality factor integrated ring resonators in the mid-infrared
Articles in the same Issue
- Frontmatter
- Research Articles
- Optical control of levitated nanoparticles via dipole–dipole interaction
- Spatio-spectral localized modal coupling for room-temperature quantum coherence protection
- Recovery of topologically robust merging bound states in the continuum in photonic structures with broken symmetry
- Localization of nanoscale objects with light singularities
- High accuracy inverse design of reconfigurable metasurfaces with transmission-reflection-integrated achromatic functionalities
- Fiber-assisted nanoparticle tracking analysis meets nanorheology: a novel approach for probing viscoelastic properties at the nanoscale
- Chiral phase-imaging meta-sensors
- Stimulator-multiplexing framework of microwave-infrared compatible reconfigurable metasurface integrated with LED array
- Optical phased array receiver with mode diversity and coherent combination
- BioMeta: modular reprogrammable metasurface for noninvasive human respiration monitoring
- Effectively suppressed reflected photonic spin Hall effect
- Letters
- Second harmonic generation of optical spin−orbit interactions in hybrid plasmonic nanocircuits
- One million quality factor integrated ring resonators in the mid-infrared

