Home Giant enhancement of optical nonlinearity from monolayer MoS2 using plasmonic nanocavity
Article Open Access

Giant enhancement of optical nonlinearity from monolayer MoS2 using plasmonic nanocavity

  • Liping Hou , Haosong Li , Qifa Wang , Xuetao Gan ORCID logo EMAIL logo , Fajun Xiao ORCID logo EMAIL logo and Jianlin Zhao ORCID logo EMAIL logo
Published/Copyright: January 19, 2024
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nanophotonics
From the journal Nanophotonics Volume 13 Issue 3

Abstract

The particle-on-mirror nanocavity, supporting multiple plasmonic resonances, provides an ideal platform to efficiently boost the nonlinear optical processes at the nanoscale. Here, we report on the enhancement of the second (SHG) and third-harmonic generations (THG) from the monolayer MoS2 using a multi-resonant Au nanosphere dimer-on-mirror nanocavity (DoMN). The strong plasmon hybridization between the dimer and underlying Au substrate leads to the emergence of two distinct cavity modes, which are intentionally aligned with the SH and TH frequencies, rendering a 15- and 68-fold enhancement for the SHG and THG of the monolayer MoS2, respectively. Further theoretical analysis yields that these remarkable nonlinearity enhancements are also ascribed to the amplification of nonlinear source because of the excellent spatial mode overlap and the high directivity of nonlinear emission enabled by the cavity modes. Our results pave the way for the implementation of low-cost, and highly efficient nonlinear photonics devices integrated with plasmonic nanocavities.

Keywords: nanoparticles; plasmonic nanocavity; monolayer MoS2 ; second- and third-harmonic generations

1 Introduction

Nanoscale nonlinear optical effects have greatly expanded the versatility of photonic applications ranging from the nonlinear optical modulator [1], [2] to nanolaser [3], super-resolution imaging [4], and biosensing [5]. However, the inherent inefficiency of nonlinear optical processes and limited active volume remain significant obstacles to the practical implementation of these applications [6], [7]. The plasmonic nanostructure possesses the capability to strongly confine light within the subwavelength volume [8], [9], making it an ideal candidate to enhance nonlinear optical processes, such as second (SHG) [10], [11], [12], [13] and third harmonic generations (THG) [14], [15]. Generally, the optical nonlinearity can be effectively enhanced by leveraging plasmonic resonances, which involve the amplification of fundamental light through strong local field interactions and/or the acceleration of nonlinear radiation via the antenna effect [14], [15], [16], [17]. In this regard, plasmonic metasurfaces fabricated by nanolithography techniques have been extensively employed to enhance the SHG of nonlinear optical materials such as two-dimensional transition metal dichalcogenides (TMDs) [18], [19], [20], [21], [22]. In particular, metasurfaces with the double-resonant feature exhibit the capability to boost the fundamental excitation and nonlinear emission simultaneously, delivery a considerable high SHG conversion efficiency [10], [23]. Nevertheless, the complex structural designs of metasurfaces typically require sophisticated and costly lithography procedures, imposing a restriction on optical nonlinearity enhancements.

Alternatively, the recently emerging particle-on-mirror (PoM) plasmonic nanocavity [24], [25], [26], [27], comprising a closely spaced nanoparticle and an ultrasmooth metal film, provides an elegant and cost-effective platform for enhancing the optical nonlinearity [28], [29]. The combination of the thin film deposition technique and the bottom–up approach enables the precise control of nanocavity size even down to the subnanometer level [30], [31], [32]. This also facilitates the integration of nonlinear optical nanomaterials such as quantum dots and TMDs [33], [34], [35], [36]. Therefore, the weak signal of nonlinear processes can be significantly magnified due to the ultrasmall mode volume and exceptional local field enhancement provided by nanocavities [33], [34]. In addition, the colloidal synthesis technique enables precise control over the size and shape of nanoparticles, offering a straightforward way to spectrally align the resonance of PoM nanocavity with the optical nonlinear processes [37], [38], [39]. Recent studies have also demonstrated that the strong plasmon–exciton coupling in TMDs-PoM hybrid systems can produce an extremely large effective second-order susceptibility in TMDs-PoM hybrid systems, rendering a 3000-fold increase in SHG intensity [40]. Besides, the deliberate selection of mode types within the PoM nanocavity allows electromagnetic symmetry-breaking induced at the SH frequency, thereby resulting in efficient and high-directional SHG emissions [28]. Of note, to expand the operation wavelength of nanophotonic devices and applications [41], it is imperative to simultaneously enhance both the SHG and THG in the hybrid PoM nanocavity system [34]. However, this area still remains largely unexplored.

To this end, we propose an Au nanosphere dimer-on-mirror nanocavity (DoMN) to enhance the SHG and THG of monolayer molybdenum disulfide (MoS2). In contrast to the single-particle nanocavity configuration, the plasmon hybridization between nanoparticles and their mirror images facilitates the generation of multiple cavity modes within the visible and near-infrared range, which can be readily adjusted to match both the SH and TH frequencies. This harmonic resonance strategy together with the merit of spatial mode overlap and high emission directivity results in a giant enhancement of SHG and THG intensities from the monolayer MoS2. Our findings present a straightforward and feasible approach to concurrently enhance the SHG and THG of monolayer MoS2, thereby paving the way for high-efficiency integrated nonlinear devices.

2 Experimental and simulation details

2.1 Sample fabrication

The Au nanosphere dimer and Au film were chosen as building blocks for the construction of the plasmonic nanocavity using the bottom-up assembly technique. Specifically, a 50-nm-thick Au film was deposited onto the silicon substrate via thermal evaporation at a deposition rate of 2 Å/s. The Au film was transferred onto the SiO2/Si substrate by a template-stripping method, rendering atomic flatness with a roughness of approximately 0.26 nm. The alumina layer, with a thickness of 5 nm, was subsequently grown onto the Au film using the atomic layer deposition technique at an operating temperature of 150 °C. The monolayer MoS2 was mechanically exfoliated from bulk crystal (HQ-graphene, Inc.), and then transferred onto the Al2O3/Au substrate with the dry transfer method. Finally, 150-nm-diameter Au nanospheres (Nanoseedz, Inc.), encapsuled with a 2 nm cetyltrimethylammonium bromide (CTAB) surfactant polymer, were spin-coated onto the monolayer MoS2 to form a MoS2-DoMN hybrid structure. It yields a nanosphere density of 0.06/μm2 on the MoS2 with an optimized separation larger than 2 μm to ensure the single-particle-level measurement.

2.2 Optical characterization

The scattering spectra of the MoS2-DoMNs were measured using a home-built dark-field confocal microscope, where the sample was illuminated with polarization-controlled white light at an incident angle of 60°. The scattering signal was collected with a 50× objective (Nikon, NA0.6). After spatially filtering with a pinhole, the scattered signal was directed to either a CCD-equipped spectrometer (Andor Shamrock SR-303IB) for spectral analysis or a CCD camera for dark-field imaging. The SHG and THG measurements were conducted using a custom-built nonlinear optical microscopy system (see Supplementary Material, Figure S1). A fiber-based pulsed laser (80 fs, 80 MHz, λ = 1550 nm) was focused onto the samples through a 100× objective (Leica, NA0.9) with a focal spot size of ∼1 μm. The nonlinear signals were collected by the same objective. After passing through a dichroic mirror, the collected SHG and THG signals were delivered to the spectrometer (HORIBA iHR320) for spectral analysis. Notably, the target dimer was first located from the SEM image, as shown the inset of Figure S2(A). By taking the edges of MoS2 flake as spatial markers, the same dimer can be identified in the dark-field image. To eliminate undesired signal contributions, dimers located at a minimum separation of 2 μm from other nanosphere clusters and the MoS2 edges were intentionally chosen in linear and nonlinear optical measurements through the pinhole.

2.3 Numerical simulation

The linear responses of the MoS2-DoMNs were calculated using the finite element method (FEM). The geometries of the MoS2-DoMNs were modeled to match their experimental counterparts. The refractive index of the Al2O3 spacer and CTAB surfactant polymer were set to be 1.5 and 1.435, respectively. The permittivity of Au was taken from the experimental data of Johnson and Christy [42]. The monolayer MoS2 was modeled as a film with a thickness of 1 nm. To accurately describe the dielectric properties of MoS2, the mesh size of the film was controlled to be below 0.2 nm, and its wavelength-dependent optical constant was obtained from the experimental data reported in Ref. [43]. For the scattering calculations, we initially employed a plane wave with an incident angle of 60° to produce the background electric field in the absence of a dimer. Subsequently, this calculated field was utilized as an excitation to derive the scattering field in the presence of the dimer. According to Gauss’s law, the charge distribution of the nanocavity was determined by evaluating the disparity in the normal component of the electric field above and below the metallic surface. The SHG and THG of the MoS2-DoMNs were calculated using a two-step method: first, the second- and third-order polarizations were derived from the linear response of the fundamental field according to P (2ω) = χ (2) E(ω)E(ω) and P (3ω) = χ (3) E(ω)E(ω)E(ω) [44], [45], [46], respectively. Then, P (2ω) and P (3ω) are regarded as nonlinear sources, which radiate the SHG and THG fields in the far-field domain (see Supplementary Material).

3 Results and discussion

The MoS2-DoMN hybrid structure is schematically depicted in Figure 1(A), which consists of an Au nanosphere dimer on top, an ultrasmooth Au film, and a monolayer MoS2. The monolayer MoS2 was identified by Raman spectroscopy carried out on a commercial confocal microscope (WITec, Alpha 300R). The interval between the out-of-plane mode A1g and in-plane mode E1 2g, as shown in Figure 1(B), is observed to be 18 cm−1, consistent with the typical mode interval in the monolayer MoS2 [47]. The bright field and scanning electron microscope (SEM) images of the hybrid structure are, respectively, displayed in Figure 1(C) and (D), where the Au dimer is marked within the white circles. The Au nanosphere radius is determined to be ∼75 nm using SEM, as clearly depicted in the inset of Figure 1(D).

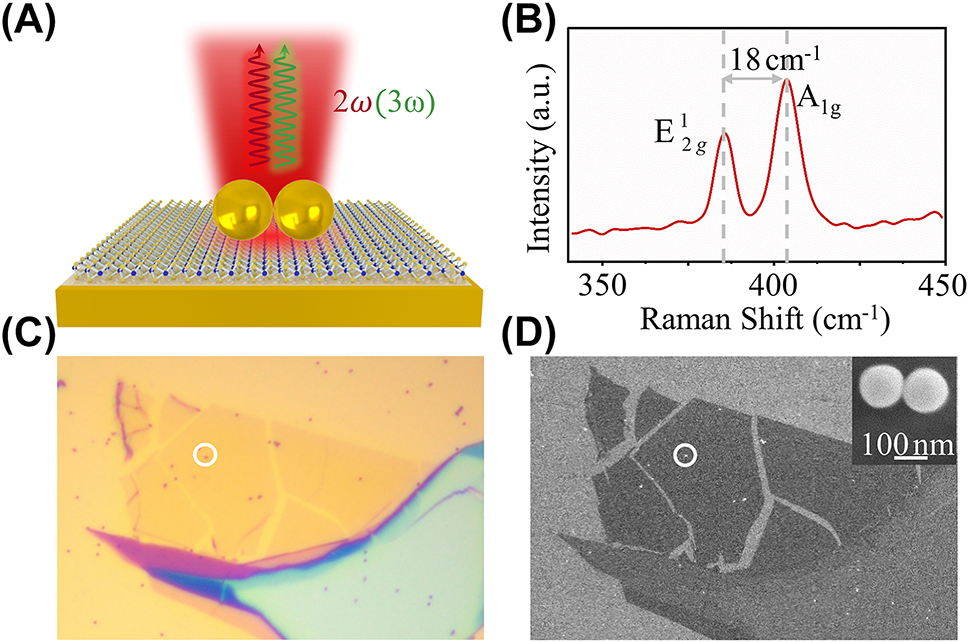
Figure 1: Hybrid structure of the monolayer MoS2 coupled Au nanosphere dimer-on-mirror nanocavity (DoMN). (A) Schematic of the monolayer MoS2-DoMN. (B) Raman spectrum of the monolayer MoS2 taken nearby the dimer. (C) Bright- and (D) SEM images of the MoS2-DoMN. The white circles indicate the location of MoS2-DoMN. The inset of (D) shows the Au nanosphere dimer, where the scale bar is 100 nm.
Figure 1:

Hybrid structure of the monolayer MoS2 coupled Au nanosphere dimer-on-mirror nanocavity (DoMN). (A) Schematic of the monolayer MoS2-DoMN. (B) Raman spectrum of the monolayer MoS2 taken nearby the dimer. (C) Bright- and (D) SEM images of the MoS2-DoMN. The white circles indicate the location of MoS2-DoMN. The inset of (D) shows the Au nanosphere dimer, where the scale bar is 100 nm.

The multi-resonance characteristic of MoS2-DoMN is revolved using the dark-field scattering spectroscopy, where the side-illumination is polarized along the dimer axis, i.e. an s-polarized beam as depicted in the inset of Figure 2(A). The scattering spectrum of the hybrid structure, as shown blue dots in Figure 2(A), exhibits 3 pronounced plasmonic modes spanning the visible and near-infrared range. This multi-resonance feature is also well reproduced by FEM simulations, as evidenced by the red solid line in Figure 2(A). To elucidate the origin of the plasmonic modes observed in Figure 2(A), we calculate the transient surface charge distributions of the hybrid structure. Here, we focus on the charge maps of mode I (∼530 nm) and II (∼750 nm), whose resonance bands can cover the SH and TH frequencies generated by the 1550 nm fundamental beam. As observed in the upper panels of Figure 2(B), the s-polarized beam induces a pronounced longitudinal plasmon coupling between two nanospheres, resulting in the formation of the bonding electric quadrupole and dipole modes in the dimer. These bonding plasmonic modes couple with their mirror-image charges in the underlying Au film, leading to the emergency of cavity modes I and II, in accordance with prior observations in the Refs. [48], [49], [50]. It should be noted that due to the asymmetry of the DoMN configuration, plasmon couplings between the dimer and Au film contribute to the nonvanishing resultant dipole moments, exhibiting considerable scattering ability as evidenced by spectral peaks in Figure 2(A). In addition, the DoMN configuration can lead to a significant reduction in radiation loss [48], [51]. Consequently, when the TH and SH wavelengths fall within the modes I and II range, the localized nonlinear source can be effectively transformed to the far-field nonlinear emission through the coupling with the resultant dipole. The low panels of Figure 2(B) show the near-field distributions of the hybrid system, which have 9- and 23-folds of field enhancement at the MoS2 plane for modes I and II, respectively. Therefore, besides the acceleration of the nonlinear radiation rate, modes I and II are expected to further augment the nonlinear signals by amplifying the TH and SH nonlinear sources.

Figure 2: Plasmonic response of MoS2-DoMNs. (A) Measured (dots) and simulated (solid line) scattering spectra of MoS2-DoMNs. The inset depicts the excitation configuration used in the measurement. (B) Charge distributions (upper panels) and electric field enhancement maps (lower panels) of modes I and II as labeled in (A).
Figure 2:

Plasmonic response of MoS2-DoMNs. (A) Measured (dots) and simulated (solid line) scattering spectra of MoS2-DoMNs. The inset depicts the excitation configuration used in the measurement. (B) Charge distributions (upper panels) and electric field enhancement maps (lower panels) of modes I and II as labeled in (A).

Subsequently, we measured the nonlinear optical responses of the MoS2-DoMN hybrid system. Here, the 1550 nm fundamental beam is kept at a constant power of 0.5 mW and polarization along the dimer axis. As expected, due to the frequencies of nonlinear emissions overlapped with the nanocavity resonances, a prominent THG and SHG signals are observed as shown the red lines in Figure 3(A) and (B). As comparisons, we perform the nonlinear measurement on the bare DoMN structure and the monolayer MoS2 on the SiO2/Si substrate, depicted as the green and blue lines in Figure 3(A) and (B). After subtracting the contribution from the DoMN structure, we define the effective enhancement factor (EF) as

(1) EF = I dim − I 0 − I dim 0 I 0

where I dim, I 0, and I dim0 are the SHG/THG intensities of the MoS2-DoMN hybrid structure, pristine monolayer MoS2, and the DoMN, respectively. According to Eq. (1), the enhancement factors are determined to be 15- and 68-folds for the SHG and THG of MoS2, respectively. We further measure the SHG and THG from 3 other MoS2-DoMN hybrid structures, yielding an averaged enhancement of 13-fold and 65-fold for SHG and THG, respectively (see Supplementary Material). The enhancements of the SHG and THG from TMDs using diverse nanostructures are summarized in Table S2. Considering that the collected nonlinear signals also include contributions from the background MoS2, the actual nonlinear responses of MoS2 enhanced by the DoMN should be large. We discussed the effective enhancement factor in the Supplementary Material. Figure 3(C) and (D), respectively, present the log-log plots of SHG and THG signals from MoS2 in the cavity as a function of the pumping power. The linear fits to these two power-dependent evolutions reveal slopes of ∼2 and ∼3, confirming the second- and third-order nature of SHG and THG nonlinear processes.

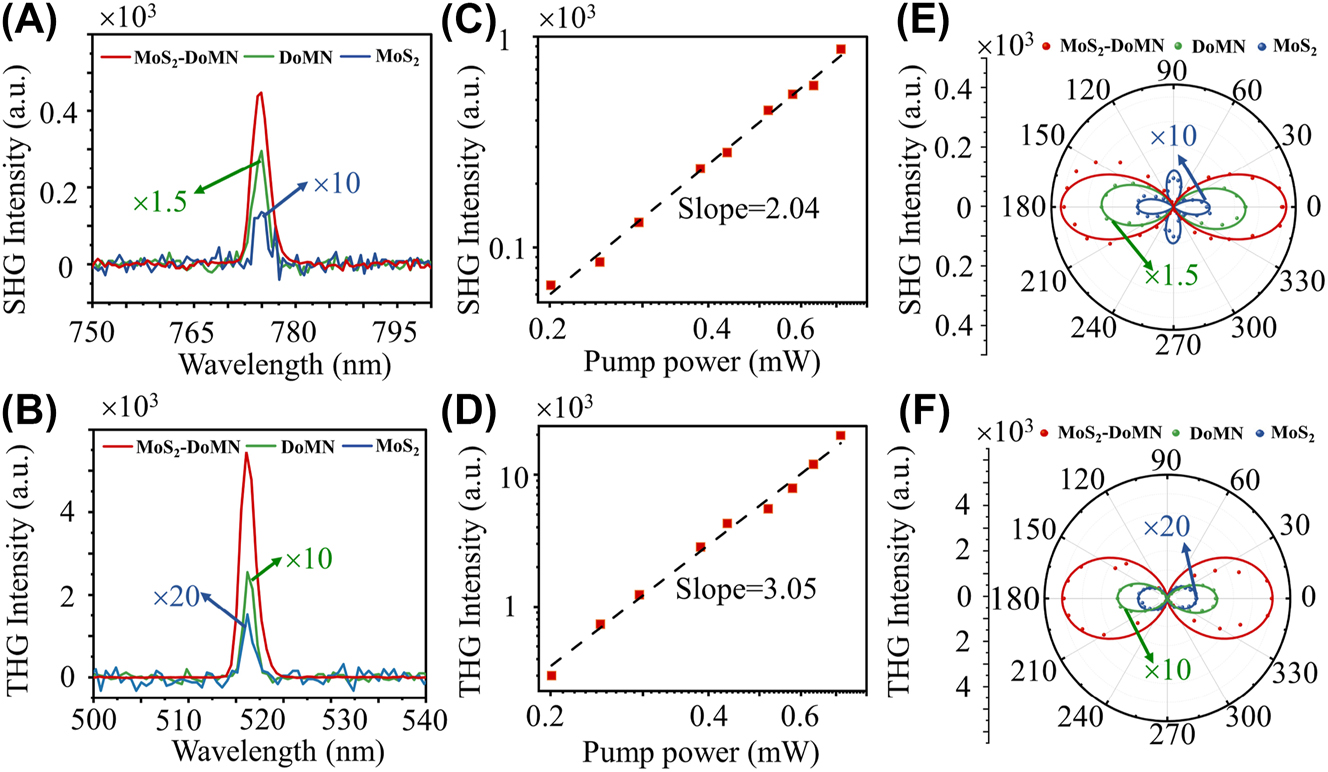
Figure 3: Characterization of nonlinear response in hybrid structures. (A) SHG and (B) THG spectra of MoS2-DoMN (red), DoMN (green), and MoS2 on SiO2/Si substrate (blue) under an excitation wavelength of 1550 nm. (C) SHG and (D) THG peak intensities as a function of laser power in a log-log plot. Polar plots of the polarization of (E) SHG and (F) THG signals from the monolayer MoS2 on SiO2/Si substrate (blue dots), DoMN (green dots), and the MoS2-DoMN (red dots). The experimental results are well-fitted by the theoretical model (solid lines).
Figure 3:

Characterization of nonlinear response in hybrid structures. (A) SHG and (B) THG spectra of MoS2-DoMN (red), DoMN (green), and MoS2 on SiO2/Si substrate (blue) under an excitation wavelength of 1550 nm. (C) SHG and (D) THG peak intensities as a function of laser power in a log-log plot. Polar plots of the polarization of (E) SHG and (F) THG signals from the monolayer MoS2 on SiO2/Si substrate (blue dots), DoMN (green dots), and the MoS2-DoMN (red dots). The experimental results are well-fitted by the theoretical model (solid lines).

The polarization-resolved analysis of plasmon-enhanced SHG and THG emissions is further investigated, as shown in Figure 3(E) and (F). We fixed the analyzer parallel to the dimer axis, while the polarization of fundamental light is rotated in a step of 5° using a half-wave plate. Because of the D 3h crystal symmetry [52], the SHG of the monolayer MoS2 on SiO2/Si substrate displays a 4-fold symmetry which is in accordance with the theoretical predictions (also see the blue line in Figure 3(E)). The polarization-dependent THG is independent on the crystal orientations of the monolayer TMDs [53], thus, showing a 2-fold symmetry for the pristine MoS2, consistent with the theoretical model (see Supplementary Material). Whereas the polar plot of SHG and THG from bare DoMN (green dots) and MoS2-DoMN (red dots) all exhibit similar two lobe pattern. The reason lies in the enhanced optical nonlinearities for both DoMN and MoS2-DoMN can be attributed to the amplification of nonlinear sources by the cavity modes I and II. The scattering spectra in Figure S4(A) demonstrate both cavity modes I and II have the same polarization dependent behavior, with the peak intensity following the two-fold symmetry (see Figure S4(B) and (C)). Consequently, the polar diagrams of nonlinear emissions from both the bare DoMN and hybrid structure exhibit two-fold symmetry patterns. These patterns show maximum intensity at 0° (180°) and 90° (270°) when cavity modes I and II are strongest or absent, respectively. These polarization-dependent features of the hybrid structure are also well described by the theoretical model (see Supplementary Material), as shown the red line in Figure 3(E) and (F).

To further unravel the role of cavity modes in the nonlinearity enhancement of monolayer MoS2, we calculate the near-field distribution of nonlinear polarization as well as their far-field radiation. As shown in Figure 4(A) and (B), both the second- and third-order polarizations exhibit crescentic distributions around the outer periphery of the touching points between the dimer and substrate. These nonlinear polarizations show a good spatial overlap with the field enhancement maps produced by cavity modes I and II at the plane of MoS2, as illustrated in Figure 4(C) and (D). Especially, the third-order polarization is localized precisely at the field maximum of cavity mode I. Therefore, the large SHG and THG enhancement can be ascribed to the substantial amplification of nonlinear sources by leveraging cavity modes, due to the excellent spatial mode matching. The far-field emission patterns of SHG and THG signals at the xz plane are presented in Figure 4(E) and (F), where the grey shaded areas indicate the collection angular of the objective (NA = 0.9). Of note, the coherent overlap between SHG from MoS2 and DoMN has a destructive interference at the up-left zone and a constructive interference and up-right zone (Figure S5), leading to an asymmetric SHG radiation of the MoS2-DoMN shown in Figure 4(E). As seen, the nonlinear signals from the SiO2/Si-supported MoS2 mainly radiate to the substrate side. In contrast, in virtue of the high radiation directivity of modes I and II, the SHG and THG of MoS2-DoMN are predominantly governed by the backward emissions, resulting in 1.96- and 2-fold increases of collection efficiency for SHG and THG, respectively.

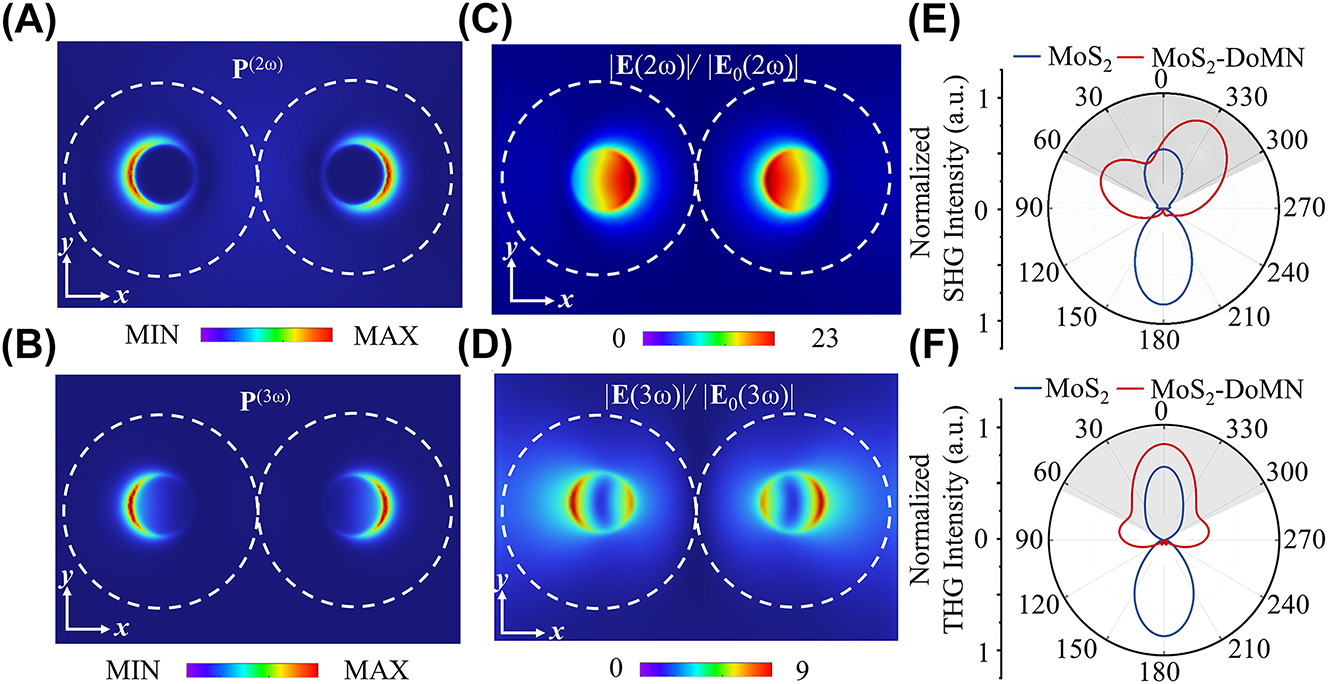
Figure 4: Nonlinear polarization distributions at (A) SH and (B) TH frequencies. Field enhancement maps of the MoS2-DoMN at the (C) SH and (D) TH frequencies. Simulated far-field radiation patterns of (E) SHG and (F) THG from the MoS2-DoMN (red curves) and MoS2 (blue curves) in the xz-plane. The gray area indicates the collection cone of the objective.
Figure 4:

Nonlinear polarization distributions at (A) SH and (B) TH frequencies. Field enhancement maps of the MoS2-DoMN at the (C) SH and (D) TH frequencies. Simulated far-field radiation patterns of (E) SHG and (F) THG from the MoS2-DoMN (red curves) and MoS2 (blue curves) in the xz-plane. The gray area indicates the collection cone of the objective.

4 Conclusions

In summary, we have proposed a method to simultaneously enhance the second (SHG) and third harmonic generations (THG) of monolayer MoS2 using a multi-resonant Au nanosphere dimer-on-mirror nanocavity (DoMN). Combining the dark-field scattering spectroscopy and full-wave simulations reveals two profound film-coupled plasmonic bonding modes in the visible and near-infrared range. These two cavity modes have a good frequency match with the SH and TH frequencies, meanwhile, ensuring an excellent spatial overlap between the nonlinear polarizations and field enhancements. These virtues work with the high emission directivity of cavity modes, delivering 15- and 68-fold of enhancement for SHG and THG of monolayer MoS2, respectively. The exceptional SHG and THG performances imply the promising prospect of our MoS2-NoMN hybrid structure in nonlinear optical applications.

Corresponding authors: Xuetao Gan, Fajun Xiao and Jianlin Zhao, Key Laboratory of Light Field Manipulation and Information Acquisition, Ministry of Industry and Information Technology, and Shaanxi Key Laboratory of Optical Information Technology, School of Physical Science and Technology, Northwestern Polytechnical University, Xi’an 710129, China, E-mail: (X. Gan), (F. Xiao), (J. Zhao) (F. Xiao)(J. Zhao)

Funding source: Fundamental Research Funds for the Central Universities

Award Identifier / Grant number: 3102019JC008

Award Identifier / Grant number: PF2023143

Funding source: National Key Research and Development Program of China

Award Identifier / Grant number: 2022YFA1404800

Funding source: National Natural Science Foundation of China

Award Identifier / Grant number: 12274345

Award Identifier / Grant number: 12374359

Award Identifier / Grant number: 62375225

Acknowledgments

The authors would like to thank the SEM measurements by the Analytical and Testing Center of Northwestern Polytechnical University.

  1. Research funding: National Key R&D Program of China (2022YFA1404800); National Natural Science Foundation of China (NSFC) (12274345, 62375225, 12374359); Fundamental Research Funds for the Central Universities (3102019JC008, PF2023143).

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: Authors state no conflicts of interest.

  4. Data availability: Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

[1] M. Klein, et al.., “2D semiconductor nonlinear plasmonic modulators,” Nat. Commun., vol. 10, no. 1, p. 3264, 2019. https://doi.org/10.1038/s41467-019-11186-w.Search in Google Scholar PubMed PubMed Central

[2] B. Huang, et al.., “Broadband mid-infrared nonlinear optical modulator enabled by gold nanorods: towards the mid-infrared regime,” Photon. Res., vol. 7, no. 6, pp. 699–704, 2019. https://doi.org/10.1364/prj.7.000699.Search in Google Scholar

[3] S. Wu, et al.., “Monolayer semiconductor nanocavity lasers with ultralow thresholds,” Nature, vol. 520, no. 7545, pp. 69–72, 2015. https://doi.org/10.1038/nature14290.Search in Google Scholar PubMed

[4] J. Liu, I.-H. Cho, Y. Cui, and J. Irudayaraj, “Second harmonic super-resolution microscopy for quantification of mRNA at single copy sensitivity,” ACS Nano, vol. 8, no. 12, pp. 12418–12427, 2014. https://doi.org/10.1021/nn505096t.Search in Google Scholar PubMed PubMed Central

[5] N. Kotov, “The only way is up,” Nat. Mater., vol. 10, no. 12, pp. 903–904, 2011. https://doi.org/10.1038/nmat3181.Search in Google Scholar PubMed

[6] M. Kauranen and A. V. Zayats, “Nonlinear plasmonics,” Nat. Photonics, vol. 6, no. 11, pp. 737–748, 2012. https://doi.org/10.1038/nphoton.2012.244.Search in Google Scholar

[7] J. R. M. Butet, P.-F. Brevet, and O. J. F. Martin, “Optical second harmonic generation in plasmonic nanostructures from fundamental principles to advanced applications,” ACS Nano, vol. 9, no. 11, pp. 10545–10562, 2015. https://doi.org/10.1021/acsnano.5b04373.Search in Google Scholar PubMed

[8] S. Viarbitskaya, et al.., “Tailoring and imaging the plasmonic local density of states in crystalline nanoprisms,” Nat. Mater., vol. 12, no. 5, pp. 426–432, 2013. https://doi.org/10.1038/nmat3581.Search in Google Scholar PubMed

[9] J. A. Schuller, E. S. Barnard, W. Cai, Y. C. Jun, J. S. White, and M. L. Brongersma, “Plasmonics for extreme light concentration and manipulation,” Nat. Mater., vol. 9, no. 3, pp. 193–204, 2010. https://doi.org/10.1038/nmat2630.Search in Google Scholar PubMed

[10] H. Aouani, et al.., “Multiresonant broadband optical antennas as efficient tunable nanosources of second harmonic light,” Nano Lett., vol. 12, no. 9, pp. 4997–5002, 2012. https://doi.org/10.1021/nl302665m.Search in Google Scholar PubMed

[11] R. Czaplicki, et al.., “Second-harmonic generation from metal nanoparticles: resonance enhancement versus particle geometry,” Nano Lett., vol. 15, no. 1, pp. 530–534, 2015. https://doi.org/10.1021/nl503901e.Search in Google Scholar PubMed

[12] J. Lee, et al.., “Giant nonlinear response from plasmonic metasurfaces coupled to intersubband transitions,” Nature, vol. 511, no. 7507, pp. 65–69, 2014. https://doi.org/10.1038/nature13455.Search in Google Scholar PubMed

[13] S. D. Liu, et al.., “Polarization-independent multiple fano resonances in plasmonic nonamers for multimode-matching enhanced multiband second-harmonic generation,” ACS Nano, vol. 10, no. 1, pp. 1442–1453, 2016. https://doi.org/10.1021/acsnano.5b06956.Search in Google Scholar PubMed

[14] B. Metzger, T. Schumacher, M. Hentschel, M. Lippitz, and H. Giessen, “Third harmonic mechanism in complex plasmonic fano structures,” ACS Photonics, vol. 1, no. 6, pp. 471–476, 2014. https://doi.org/10.1021/ph5000677.Search in Google Scholar PubMed PubMed Central

[15] C. Ciracì, M. Scalora, and D. R. Smith, “Third-harmonic generation in the presence of classical nonlocal effects in gap-plasmon nanostructures,” Phys. Rev. B, vol. 91, no. 20, p. 205403, 2015. https://doi.org/10.1103/physrevb.91.205403.Search in Google Scholar

[16] A. Noor, A. R. Damodaran, I. H. Lee, S. A. Maier, S. H. Oh, and C. Ciraci, “Mode-matching enhancement of second-harmonic generation with plasmonic nanopatch antennas,” ACS Photonics, vol. 7, no. 12, pp. 3333–3340, 2020. https://doi.org/10.1021/acsphotonics.0c01545.Search in Google Scholar PubMed PubMed Central

[17] B. Metzger, L. Gui, J. Fuchs, D. Floess, M. Hentschel, and H. Giessen, “Strong enhancement of second harmonic emission by plasmonic resonances at the second harmonic wavelength,” Nano Lett., vol. 15, no. 6, pp. 3917–3922, 2015. https://doi.org/10.1021/acs.nanolett.5b00747.Search in Google Scholar PubMed

[18] Y. Ding, et al.., “Second harmonic generation covering the entire visible range from a 2D material-plasmon hybrid metasurface,” Adv. Opt. Mater., vol. 9, no. 16, p. 2100625, 2021. https://doi.org/10.1002/adom.202100625.Search in Google Scholar

[19] Q. Leng, et al.., “Enhanced second-harmonic generation in monolayer MoS2 on suspended metallic nanostructures by plasmonic resonances,” Nanophotonics, vol. 10, no. 7, pp. 1871–1877, 2021. https://doi.org/10.1515/nanoph-2021-0030.Search in Google Scholar

[20] J. Shi, et al.., “Plasmonic enhancement and manipulation of optical nonlinearity in monolayer tungsten disulfide,” Laser Photon. Rev., vol. 12, no. 10, p. 1800188, 2018. https://doi.org/10.1002/lpor.201800188.Search in Google Scholar

[21] F. Spreyer, C. Ruppert, P. Georgi, and T. Zentgraf, “Influence of plasmon resonances and symmetry effects on second harmonic generation in WS2-plasmonic hybrid metasurfaces,” ACS Nano, vol. 15, no. 10, pp. 16719–16728, 2021. https://doi.org/10.1021/acsnano.1c06693.Search in Google Scholar PubMed

[22] Z. Wang, et al.., “Selectively plasmon-enhanced second-harmonic generation from monolayer tungsten diselenide on flexible substrates,” ACS Nano, vol. 12, no. 2, pp. 1859–1867, 2018. https://doi.org/10.1021/acsnano.7b08682.Search in Google Scholar PubMed

[23] M. Celebrano, et al.., “Mode matching in multiresonant plasmonic nanoantennas for enhanced second harmonic generation,” Nat. Nanotechnol., vol. 10, no. 5, pp. 412–417, 2015. https://doi.org/10.1038/nnano.2015.69.Search in Google Scholar PubMed

[24] C. Li, et al.., “Enhanced photoluminescence of monolayer MoSe2 in a double resonant plasmonic nanocavity with fano resonance and mode matching,” Laser Photon. Rev., vol. 16, no. 2, p. 2100199, 2021. https://doi.org/10.1002/lpor.202100199.Search in Google Scholar

[25] R. Chikkaraddy, et al.., “Single-molecule strong coupling at room temperature in plasmonic nanocavities,” Nature, vol. 535, no. 7610, pp. 127–130, 2016. https://doi.org/10.1038/nature17974.Search in Google Scholar PubMed PubMed Central

[26] J. J. Baumberg, J. Aizpurua, M. H. Mikkelsen, and D. R. Smith, “Extreme nanophotonics from ultrathin metallic gaps,” Nat. Mater., vol. 18, no. 7, pp. 668–678, 2019. https://doi.org/10.1038/s41563-019-0290-y.Search in Google Scholar PubMed

[27] M. E. Kleemann, et al.., “Strong-coupling of WSe2 in ultra-compact plasmonic nanocavities at room temperature,” Nat. Commun., vol. 8, no. 1, p. 1296, 2017. https://doi.org/10.1038/s41467-017-01398-3.Search in Google Scholar PubMed PubMed Central

[28] G.-C. Li, D. Lei, M. Qiu, W. Jin, S. Lan, and A. V. Zayats, “Light-induced symmetry breaking for enhancing second-harmonic generation from an ultrathin plasmonic nanocavity,” Nat. Commun., vol. 12, no. 1, p. 4326, 2021. https://doi.org/10.1038/s41467-021-24408-x.Search in Google Scholar PubMed PubMed Central

[29] S. Shen, et al.., “Plasmon-enhanced second-harmonic generation nanorulers with ultrahigh sensitivities,” Nano Lett., vol. 15, no. 10, pp. 6716–6721, 2015. https://doi.org/10.1021/acs.nanolett.5b02569.Search in Google Scholar PubMed

[30] Q. Wang, et al.., “Unveiling radial breathing mode in a particle-on-mirror plasmonic nanocavity,” Nanophotonics, vol. 11, no. 3, pp. 487–494, 2022. https://doi.org/10.1515/nanoph-2021-0506.Search in Google Scholar

[31] J. Sun, et al.., “Light-emitting plexciton: exploiting plasmon-exciton interaction in the intermediate coupling regime,” ACS Nano, vol. 12, no. 10, pp. 10393–10402, 2018. https://doi.org/10.1021/acsnano.8b05880.Search in Google Scholar PubMed

[32] R. Chikkaraddy, et al.., “How ultranarrow gap symmetries control plasmonic nanocavity modes: from cubes to spheres in the nanoparticle-on-mirror,” ACS Photonics, vol. 4, no. 3, pp. 469–475, 2017. https://doi.org/10.1021/acsphotonics.6b00908.Search in Google Scholar

[33] X. Han, et al.., “Harmonic resonance enhanced second-harmonic generation in the monolayer WS2-Ag nanocavity,” ACS Photonics, vol. 7, no. 3, pp. 562–568, 2020. https://doi.org/10.1021/acsphotonics.9b01499.Search in Google Scholar

[34] J. Shi, Z. Lin, Z. Zhu, J. Zhou, G. Q. Xu, and Q. H. Xu, “Probing excitonic rydberg states by plasmon enhanced nonlinear optical spectroscopy in monolayer WS2 at room temperature,” ACS Nano, vol. 16, no. 10, pp. 15862–15872, 2022. https://doi.org/10.1021/acsnano.2c02276.Search in Google Scholar PubMed

[35] M. R. Singh, “Enhancement of the second-harmonic generation in a quantum dot-metallic nanoparticle hybrid system,” Nanotechnology, vol. 24, no. 12, p. 125701, 2013. https://doi.org/10.1088/0957-4484/24/12/125701.Search in Google Scholar PubMed

[36] H. Hong, et al.., “Giant enhancement of optical nonlinearity in two-dimensional materials by multiphoton-excitation resonance energy transfer from quantum dots,” Nat. Photonics, vol. 15, no. 7, pp. 510–515, 2021. https://doi.org/10.1038/s41566-021-00801-2.Search in Google Scholar

[37] S. J. Ding, et al.., “Magnetic plasmon-enhanced second-harmonic generation on colloidal gold nanocups,” Nano Lett., vol. 19, no. 3, pp. 2005–2011, 2019. https://doi.org/10.1021/acs.nanolett.9b00020.Search in Google Scholar PubMed

[38] T. Zhou, et al.., “Synthesis of AuAg/Ag/Au open nanoshells with optimized magnetic plasmon resonance and broken symmetry for enhancing second-harmonic generation,” Nanoscale, vol. 13, no. 46, pp. 19527–19536, 2021. https://doi.org/10.1039/d1nr04814g.Search in Google Scholar PubMed

[39] Y. Zeng, H. Qian, M. J. Rozin, Z. Liu, and A. R. Tao, “Enhanced second harmonic generation in double-resonance colloidal metasurfaces,” Adv. Funct. Mater., vol. 28, no. 51, p. 1803019, 2018. https://doi.org/10.1002/adfm.201803019.Search in Google Scholar

[40] T. Zhang, Q. Guo, Z. Shi, S. Zhang, and H. Xu, “Coherent second harmonic generation enhanced by coherent plasmon-exciton coupling in plasmonic nanocavities,” ACS Photonics, vol. 10, no. 5, pp. 1529–1537, 2023. https://doi.org/10.1021/acsphotonics.3c00105.Search in Google Scholar

[41] A. Autere, H. Jussila, Y. Dai, Y. Wang, H. Lipsanen, and Z. Sun, “Nonlinear optics with 2D layered materials,” Adv. Mater., vol. 30, no. 24, p. 1705963, 2018. https://doi.org/10.1002/adma.201705963.Search in Google Scholar PubMed

[42] P. B. Johnson and R. W. Christy, “Optical constants of the noble metals,” Phys. Rev. B, vol. 6, no. 12, pp. 4370–4379, 1972. https://doi.org/10.1103/physrevb.6.4370.Search in Google Scholar

[43] K. M. Islam, R. Synowicki, T. Ismael, I. Oguntoye, N. Grinalds, and M. D. Escarra, “In-plane and out-of-plane optical properties of monolayer, few-layer, and thin-film MoS2 from 190 to 1700 nm and their application in photonic device design,” Adv. Photon. Res., vol. 2, no. 5, p. 2000180, 2021. https://doi.org/10.1002/adpr.202000180.Search in Google Scholar

[44] G. Bachelier, J. Butet, I. Russier-Antoine, C. Jonin, E. Benichou, and P. F. Brevet, “Origin of optical second-harmonic generation in spherical gold nanoparticles: local surface and nonlocal bulk contributions,” Phys. Rev. B, vol. 82, no. 23, p. 235403, 2010. https://doi.org/10.1103/physrevb.82.235403.Search in Google Scholar

[45] R. W. Boyd, Nonlinear Optics, 4th ed. an imprint of Elsevier. London, United Kingdom, Academic Press, 2020.Search in Google Scholar

[46] A. Saynatjoki, et al.., “Ultra-strong nonlinear optical processes and trigonal warping in MoS2 layers,” Nat. Commun., vol. 8, no. 1, p. 893, 2017. https://doi.org/10.1038/s41467-017-00749-4.Search in Google Scholar PubMed PubMed Central

[47] C. Lee, H. Yan, L. E. Brus, T. F. Heinz, J. Hone, and S. Ry, “Anomalous lattice vibrations of single- and few-layer MoS2,” ACS Nano, vol. 4, no. 5, pp. 2695–2700, 2010. https://doi.org/10.1021/nn1003937.Search in Google Scholar PubMed

[48] G. C. Li, Y. L. Zhang, J. Jiang, Y. Luo, and D. Y. Lei, “Metal-substrate-mediated plasmon hybridization in a nanoparticle dimer for photoluminescence line-width shrinking and intensity enhancement,” ACS Nano, vol. 11, no. 3, pp. 3067–3080, 2017. https://doi.org/10.1021/acsnano.7b00048.Search in Google Scholar PubMed

[49] G. C. Li, Y. L. Zhang, and D. Y. Lei, “Hybrid plasmonic gap modes in metal film-coupled dimers and their physical origins revealed by polarization resolved dark field spectroscopy,” Nanoscale, vol. 8, no. 13, pp. 7119–7126, 2016. https://doi.org/10.1039/c5nr09260d.Search in Google Scholar PubMed

[50] Q. Zhang, G. C. Li, T. W. Lo, and D. Y. Lei, “Polarization-resolved optical response of plasmonic particle-on-film nanocavities,” J. Opt., vol. 20, no. 2, p. 024010, 2018. https://doi.org/10.1088/2040-8986/aaa1bc.Search in Google Scholar

[51] G.-C. Li, Q. Zhang, S. A. Maier, and D. Lei, “Plasmonic particle-on-film nanocavities: a versatile platform for plasmon-enhanced spectroscopy and photochemistry,” Nanophotonics, vol. 7, no. 12, pp. 1865–1889, 2018. https://doi.org/10.1515/nanoph-2018-0162.Search in Google Scholar

[52] D. Li, et al.., “Anisotropic enhancement of second-harmonic generation in monolayer and bilayer MoS2 by integrating with TiO2 nanowires,” Nano Lett., vol. 19, no. 6, pp. 4195–4204, 2019. https://doi.org/10.1021/acs.nanolett.9b01933.Search in Google Scholar PubMed

[53] X. Wen, Z. Gong, and D. Li, “Nonlinear optics of two-dimensional transition metal dichalcogenides,” InfoMat, vol. 1, no. 3, pp. 317–337, 2019. https://doi.org/10.1002/inf2.12024.Search in Google Scholar

Supplementary Material

This article contains supplementary material (https://doi.org/10.1515/nanoph-2023-0714).

Received: 2023-10-19
Accepted: 2024-01-08
Published Online: 2024-01-19

© 2024 the author(s), published by De Gruyter, Berlin/Boston

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Frontmatter
  2. Research Articles
  3. Low sidelobe silicon optical phased array with Chebyshev amplitude distribution
  4. Identifying topology of leaky photonic lattices with machine learning
  5. Can photonic heterostructures provably outperform single-material geometries?
  6. Strongly subradiant states in planar atomic arrays
  7. Spatially inhomogeneous inverse Faraday effect provides tunable nonthermal excitation of exchange dominated spin waves
  8. Micro-nano hierarchical urchin-like ZnO/Ag hollow sphere for SERS detection and photodegradation of antibiotics
  9. Optical mode-controlled topological edge state in waveguide lattice
  10. Electrically-switched differential microscopy based on computing liquid-crystal platforms
  11. Fabrication of 1 × N integrated power splitters with arbitrary power ratio for single and multimode photonics
  12. Giant enhancement of optical nonlinearity from monolayer MoS2 using plasmonic nanocavity
  13. Manipulating chiral photon generation from plasmonic nanocavity-emitter hybrid systems: from weak to strong coupling
  14. Over a thousand-fold enhancement of the spontaneous emission rate for stable core−shell perovskite quantum dots through coupling with novel plasmonic nanogaps
  15. Coherent perfect loss with single and broadband resonators at photonic crystal nanobeam
https://doi.org/10.1515/nanoph-2023-0714
Keywords for this article
nanoparticles; plasmonic nanocavity; monolayer MoS2; second- and third-harmonic generations
Creative Commons
BY 4.0

Articles in the same Issue

  1. Frontmatter
  2. Research Articles
  3. Low sidelobe silicon optical phased array with Chebyshev amplitude distribution
  4. Identifying topology of leaky photonic lattices with machine learning
  5. Can photonic heterostructures provably outperform single-material geometries?
  6. Strongly subradiant states in planar atomic arrays
  7. Spatially inhomogeneous inverse Faraday effect provides tunable nonthermal excitation of exchange dominated spin waves
  8. Micro-nano hierarchical urchin-like ZnO/Ag hollow sphere for SERS detection and photodegradation of antibiotics
  9. Optical mode-controlled topological edge state in waveguide lattice
  10. Electrically-switched differential microscopy based on computing liquid-crystal platforms
  11. Fabrication of 1 × N integrated power splitters with arbitrary power ratio for single and multimode photonics
  12. Giant enhancement of optical nonlinearity from monolayer MoS2 using plasmonic nanocavity
  13. Manipulating chiral photon generation from plasmonic nanocavity-emitter hybrid systems: from weak to strong coupling
  14. Over a thousand-fold enhancement of the spontaneous emission rate for stable core−shell perovskite quantum dots through coupling with novel plasmonic nanogaps
  15. Coherent perfect loss with single and broadband resonators at photonic crystal nanobeam
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 12.11.2025 from https://www.degruyterbrill.com/document/doi/10.1515/nanoph-2023-0714/html?lang=en
Scroll to top button