Plasmons compressing the light – a jewel in the treasure chest of Mark Stockman’s legacy

1 Introduction

Professor Mark I. Stockman of Georgia State University, a towering figure in photonics and a force behind numerous trailblazing advances in nanophotonics, and more specifically plasmonics, passed away in November 2020. It will take time for the world of science to recognize what a significant and irreparable loss it has been and to properly assess the breadth and depths of Mark’s contributions made over the course of five decades. Still, it is not too early to recognize Mark’s key contributions that have the deepest impact on the course of progress in photonics.

Mark’s work on coherent sources of surface plasmons (SPASER) [1, 2] is probably the most widely recognized one, but it would be a great disservice to his legacy to omit other, in my view, no less important contributions to nanophotonics. Among them, his innovative ideas in the field of nanoscopy and nanofocusing do stand out and thus deserve a special attention. The whole idea of nanofocusing (i.e. concentrating the light into subwavelength volumes) using photonic and plasmonic nanoscale structures has been discussed for many years [3], but it took Mark Stockman to bring it closer to reality when he first introduced concepts of adiabatic focusing [4] and focusing using selfsimilar chains of nanoparticles [5]. These ideas have been further developed by the community and have established the means of both effective focusing of light into miniscule volumes [6] and, most remarkably, accelerating by orders of magnitudes the spontaneous emission rates via the Purcell effect [7, 8]. These achievements are already finding applications in nanoscale sensing and in the development of efficient single photon sources.

In 2003 Mark Stockman, working with colleagues Kuiru Li and David Bergman, was the first one to come up with this groundbreaking idea that using a chain of selfsimilar (i.e. having the same shape) nanoparticles with progressively decreasing sizes can focus the light into the gap between the smallest nanospheres where the local fields are enhanced by orders of magnitude [5]. In this work Mark and his colleagues skillfully utilized the fact that the resonant frequencies of subwavelength localized surface plasmons (LSPs) depend only on the shape and not on the size of the modes, and that allows efficient resonant transfer of power along the chain in both directions; i.e. it can enhance both absorption and emission of light.

Shortly thereafter, in 2004 Mark expanded the concept of adiabatic light concentration to propagating surface plasmon polaritons (SPPs) in the tapered plasmonic waveguide, and it is this type of light concentration that has become known as “nanofocusing” in a narrow sense. As the width of the waveguide and the effective wavelength of SPP are reduced, the impedance gradually increases and reaches values almost comparable to those of atomic and molecular dipoles. The key to efficient transfer of energy is the fact that the width (and hence impedance) are changing adiabatically; hence the reflection is almost nonexistent and the only limitation to efficiency is metal absorption. In his work Mark has taken previous work on polariton nanofocusing [9] farther along to practical implementations achieved since his pioneering contribution [6].

Concurrently with the aforementioned work on light concentration, Mark Stockman (in collaboration with Peter Nordlander’s group at Rice University) has pointed that significant enhancement can be attained in plasmonic dimers. As discussed in [10] the dimer acts as an optical antenna with low impedance while its gap mode acts as a high impedance cavity [11] and was exploited in achieving record high emission rates for quantum emitters [8].

And yet, despite the large number of experimental results, computer models, and theoretical analyses, the question of what kind of ultimate enhancement can be attained using the principle of adiabatic nanofocusing remains open. Furthermore, various groups approach it from different angles. Some, approaches that can be traced to electromagnetic (EM) theory emphasize the impedance matching between antenna and atom or molecule (to which we shall refer as a quantum oscillator) [12], [13], [14], while others concentrate on local density of states [15], and yet other approaches treat the complex plasmonic structures as coupled oscillators [11, 16]. The nanophotonics community could benefit from a unified theory of adiabatic nanofocusing (and the reverse process of emission enhancement) which would show the equivalence of different approaches using a very simple and transparent model in a way Mark Stockman always presented his work, i.e. with clarity, depth, and succinctness. These days computing power at our disposal allows us to resolve many physical problems with speed and efficiency which would have been seen beyond the realm of possible only a few decades ago. But with the growing preponderance of numerical method something is in danger of being lost. That something is the ability to present a simple a clear picture of the physics behind complicated phenomena, and it is this ability that made Mark Stockman stand out among his peers. Alas, Mark is no longer available to undertake this task, so, this paper is an attempt to explain light concertation on nanoscale to a wide audience to the best of my rather modest abilities, with a hope that this work will serve as a tribute to Mark’s rich legacy.

This work has been conceived as neither a review nor a comprehensive tutorial. It combines previously known concepts with a number of new insights which may help the reader to get an intuitive feel for nanofocusing and appreciate Mark Stockman’s foresight. Plasmonics is a truly multidisciplinary science and the same problem of light concentrating can be approached from the point of view of electrical engineer (impedance matching), quantum optics (density of states), or physical optics (absorption and emission cross-sections). Here I attempt to show how all these approaches lead to the same results, which, in my view has certain pedagogical value. First I briefly review the idea of nanofocusing as impedance matching between free space and the quantum oscillator. Then a coupled oscillator model will be described to explain the energy concentration in plasmonic dimers and trimers. A novel concept of coupled mode having two different “effective volumes” – one as a cavity and one as an antenna – will be developed and related to the local density of states. A coupled mode model will be then further extended to the “hybrid modes” incorporating quantum oscillators and metallic nanoparticles. It will be shown that ultimately the degree of enhancement is limited by the minimum size of the smallest nanoparticle (∼10 nm) at which the onset of Landau damping broadens the linewidth of resonance and thus limits the enhancement. The last section contains the conclusions that further emphasize foresight of Mark Stockman and his contribution to nanophotonics.

2 Quantum oscillator and its impedance

The quantum oscillator, which can be an atom, a molecule, and exciton, or a quantum dot, and can be both an absorber and emitter, was first treated as a two-level system by Greffet et al. in [14]. The impedance was introduced using Green’s function and related to local density of states. Here the somewhat different approach leading to the same circuit model is considered. In the presence of external field E_ext with frequency ω the two level system with resonant frequency ω ₂₁ and transition matrix element r 12 = 〈 1 | r | 2 〉 , shown in Figure 1a, develops a dipole moment

where γ _a is the dephasing rate. The physical size (effective radius) of the oscillator can be approximated as r a = 〈 1 | r 2 | 1 〉 1 / 2 and then the current “flowing through the quantum oscillator” is I a ∼ − i ω p a / 2 r a , while the voltage on it is roughly V a ∼ 2 r a E a . Hence the impedance can be found as

where G 0 = 2 e 2 / h = 7.75 × 10 − 5 S is quantum conductance. Introducing the oscillator strength f 12 = 2 m 0 ω 12 r 12 2 / 3 ℏ and using the typical relation between transition frequency and the effective radius ℏ ω 21 ∼ ℏ 2 / 2 m 0 r a 2 we obtain

with three terms inside the brackets corresponding to the resistance, inductance, and capacitance, all connected in series (Figure 1a), as first noted in [14].

Figure 1:

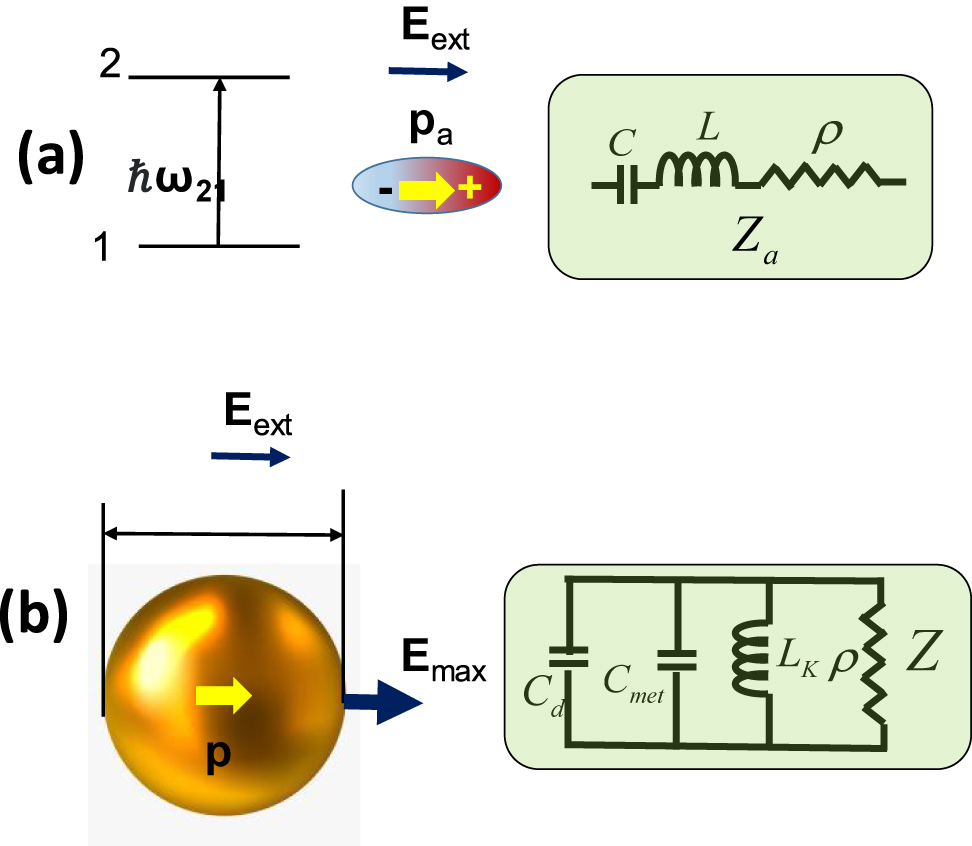
(a) Two-quantum oscillator and its circuit model, (b) localized surface plasmon (LSP) mode on a metal nanoparticle and its circuit model.

On resonance one obtains

where Q a = ω 12 / γ , α 0 = 1 / 137 is the fine structure constant and η 0 = 377 Ω is the vacuum impedance. With a reasonably high Q the impedance of the quantum oscillator is on the order of η ₀, however when one considers transfer of energy in space, it is the impedance per unit area that matters [14, 17], i.e. dividing (2) by r a 2 obtains on resonance

r 12 ∼ 1 Å for the allowed transitions in the visible/near infrared (IR) region of spectrum and assuming Q in the 10¹–10³ range one obtains Z a ′ ∼ 1 − 100 k Ω / nm 2 . This result is similar to the one obtained in [14] using Green’s function, albeit obtained using classical dipole analogy. At the same time the impedance per unit area of the free space is [14]

The impedance mismatch between the quantum oscillator and free space is therefore

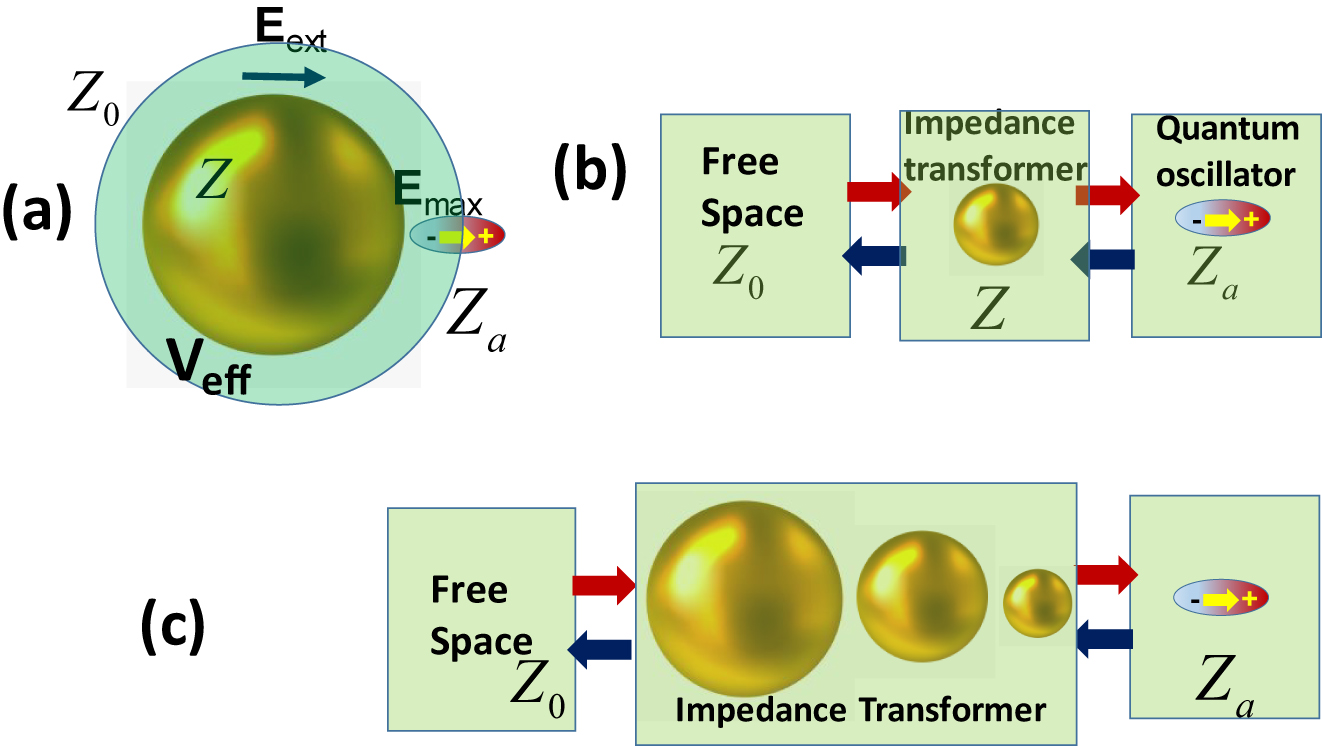
or anywhere between 6 and 8 orders of magnitude, even for the allowed transition, and more than that for weaker, forbidden transition. (Note that this mismatch is essentially a ratio between the diameter of diffraction limited focused beam and resonant absorption cross-section of the atom or molecule indicating the connection between the electrical engineering and physical optics approaches). Clearly, to match impedances one has to resort to using an antenna that serves as impedance transformer. Such a transformer can be a nanoparticle supporting the LSP. Intuitively the dimensions of that mode should be on the order of the geometric mean between wavelength and atomic dipole, i.e. few tens of nanometers.

3 Nanofocusing as impedance matching

Let us now determine the impedance of an LSP of the plasmonic nanoparticle shown in Figure 1b. A spherical nanoparticle with a diameter d is shown in Figure 1b, but the theory developed here can be easily applied to the other shapes. Following the theory of Engheta and Alu [12], we consider a nanoparticle made from a metal with dielectric constant ϵ m ( ω ) = ϵ r b − ω p 2 / ( ω 2 + j ω γ ) , where ε _rb is the “background” permittivity associated with interband transitions, ω _p is the plasma frequency, and γ is the scattering rate in metal, surrounded by a dielectric with relative permittivity ε _d . The AC conductivity of metal is

The first term corresponds to the capacitance, C _mat the second to the kinetic inductance, L _K and the last one to the resistance ρ, all connected in parallel as displayed in Figure 1b. In addition, there is also a capacitance associated with the field in the dielectric C _d . The capacitance scales with diameter d while inductance and resistance are inversely proportional to it. Overall, assuming ω ≫ γ we can write for the impedance

where coefficients B _c and B _L are shape-dependent coefficients, both on the order of unity and coefficient β corresponds to the fraction of electric field in the dielectric. Clearly the resonance occurs when

For the spherical particle one can show that B _C =B _L and β=2 so that a familiar expression for the LSP resonance emerges

On resonance

As one can see, the impedance decreases dramatically with the size of the nanoparticle. It should also be noted that the resonant frequency does not depend on the actual size of the nanoparticle because in (9) we neglect the “normal” inductance due to magnetic field induced by the current in the metal, L M ∼ μ 0 d “connected in series” with kinetic inductance L K ∼ 1 / ω p 2 ϵ 0 d . One can see that L _K =L _M when d ∼ λ p / 2 π , i.e. is equal to the skin depth which amounts to less than 100 nm. Therefore the above results are valid only for d < 100 nm . For larger nanoparticles the resonance shifts to the red part of the spectrum and eventually the impedance becomes

leading to the resonance condition ω 0 ∼ c / ϵ d 1 / 2 d , i.e. resonance being determined by the size (length) rather than by the material. In other words, one deals with an antenna rather than with a “plasmon.” But as long as we operate in the plasmonic regime the impedance (12) decreases with the size of nanoparticle as Z ∼ d − 1 .

Now, when one considers impedance mismatch one has to realize that the energy transfer takes place only across a fraction of the surface; hence it makes sense to define the impedance per unit area as shown in [14]

i.e. proportional to the effective local density of states ρ ∼ Q / V ω . Therefore, matching the impedance is equivalent to matching the densities of states, a fact first noticed by Novotny [15, 18]. If one places the quantum oscillator near the surface of the nanoparticle as shown in Figure 2a, the local field enhancement will facilitate energy transfer to the quantum oscillator thus enhancing absorption [19]. The same enhancement will of course be observed in the emission as spontaneous emission gets enhanced by the Purcell effect [20, 21]. From the point of view of circuit modeling, the nanoparticle serves as an impedance transformer as outlined in Figure 2b. Intuitively following circuit theory, one can expect to achieve impedance match when the impedance of LSP mode in nanoparticle Z ′ = Z a ′ Z o ′ , and characteristic size of the nanoparticle is

for a wide range of Q’s. These numbers are not far from the ones found optimal in [19, 21], but it has also been shown this does not lead to the absorption (emission) enhancement exceeding 4 Q 2 i.e. a factor of about 10⁴–10⁵. Therefore, if one uses the circuit analogy further, the impedance matching will improve if one uses chain impedance transformers as shown in Figure 2c – a suggestion first made by Mark Stockman and coworkers in [5]. The crude estimate of the field enhancement is then that each successive step of nanofocusing enhances absorption by another factor of 4 A 2 Q 2 and in principle one can expect a really enormous enhancement of absorption and Purcell factor. But that assessment neglects the fact that the range of the particle dimensions is limited on both sides. As size of nanoparticle exceeds about 100 nm, radiative loss becomes the chief source of damping. At the same time when the nanoparticle dimensions become smaller than 5–10 nm, Landau damping [22], [23], [24], [25], which also can be thought of as a surface-assisted absorption [26, 27] sets in causing increase of loss and reduction of Q.

Figure 2:

(a) LSP mode enhancing field near the quantum oscillator, (b) circuit model of absorption/emission enhancement as impedance matching and (c) impedance matching with a chain of nanoparticles.

The rest of this paper is devoted to exploring focusing with plasmonic dimers [28] and trimers [29]. While using impedances conveniently relates the issue to the classical impedance matching in electrical engineering, it is also worthwhile to explore the same issue from a different point of view – by developing an analytical coupled mode model for the chain of nanoparticles [30], [31], [32]. Previously, this model has only been used for plasmonic dimers and the role of damping was not explored, but in this work it is extended to three and more nanoparticles. Doing so allows one to see clearly how the adiabaticity allows one to increase degree of field enhancement, and to concurrently explore the limits of this enhancement

4 Coupled modes theory – plasmonic dimer

First, one shall note that the dipole moment of the LSP on a nanosphere of Figure 2a is

where E ext ( t ) is the external field. By assuming that one operates close to the resonance, ϵ m ( ω 0 ) ≈ − 2 ϵ d , we obtain

where the LSP resonant frequency ω ₀ is given in (11) and the DC polarizability is

(for the case when ϵ r b = ϵ d = 1 , α = 3 ϵ 0 V ). It is clear that (17) is a solution of a differential equation for a driven harmonic oscillator

Now, it is possible to relate the dipole and the total energy of the LSP mode as

where a new variable a is a square root of energy in LSP mode (classical analogue of plasmon annihilation operator). Now

and (19) becomes

where

It is also possible to relate a to the magnitude of the electric field on the surface of the nanoparticle,

and introduce the effective volume

so that

Finally, one obtains

Where the “material” factor is

For ϵ r b = ϵ d = 1 , A=2, and for other, non-spherical shapes A, renamed as “material and shape factor”,will still be on the order of unity. Note that at resonance a=iα ₁ QE_ext, and therefore

where the maximum enhancement by a single nanoparticle F ₁=AQ. Thus with a single nanoparticle maximum field enhancement is just on the order of Q factor, i.e. no more than 10–20 times. Note that the ratio between the effective volume and nanoparticle volume (25) can be written as V eff = 3 V ϵ d 2 / 2 A , i.e. the two volumes roughly have the same order of magnitude.

Let us now consider coupling between two nanoparticles separated by distance r ₁₂, as shown in Figure 3a. The field of the larger nanoparticle at the center of the smaller nanoparticle is

and the coupling coefficient is obtained by substituting (30) into (22)

where K = V 1 / V 2 . It is easy to see that κ ₂₁=κ ₁₂=κ, hence one can write coupled mode equations

Figure 3:

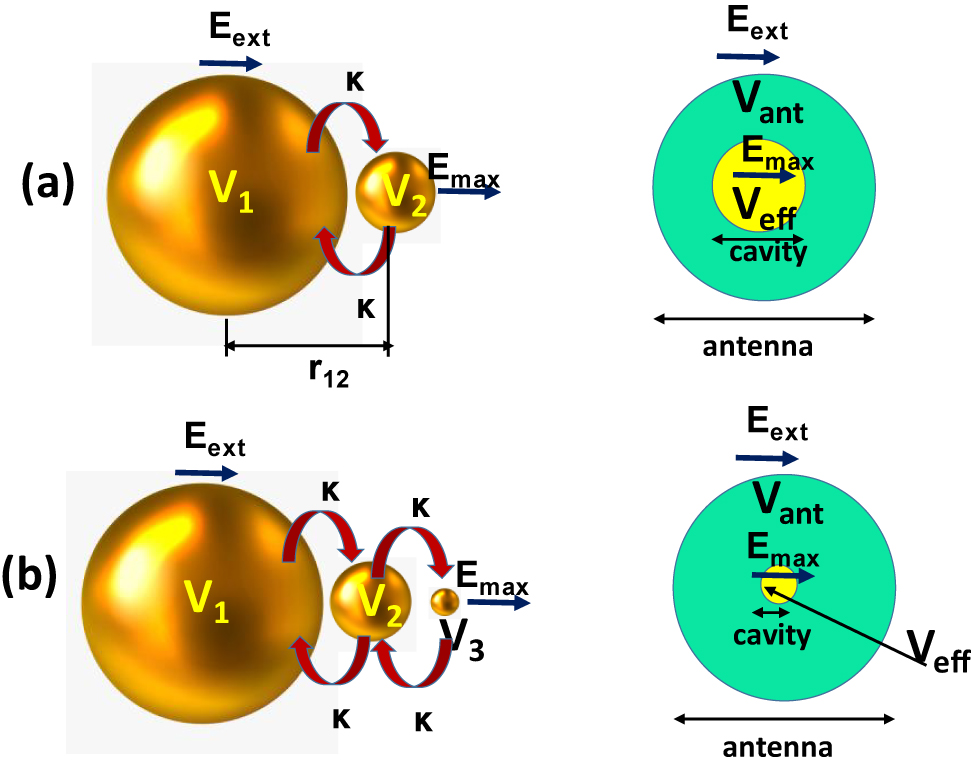
Energy transfer in (a) plasmonic dimer and (b) plasmonic trimer. On the right hand side the couple modes are represented as oscillators with large volume as an antenna V ant (important for coupling to the free space) and small volume as a cavity V _eff (important for coupling to quantum oscillators).

Now if one introduces symmetric and antisymmetric super-modes

adding and subtracting two lines in (32) yields

The “effective polarizabilities” for two super-modes are

where the “effective volume as an antenna” has been introduced as

Clearly, for vastly dissimilar nanoparticles V s ( a ) , ant ≈ V 1 , eff / 2 hence the dimer’s mode performance as an antenna is determined by the larger nanoparticle in the dimer as seen in Figure 3a. The steady state solutions of (34) are

Now, effective volume as a cavity for each mode can be found from the fact that the energy is equally divided between two nanoparticles, and since the maximum field is at the surface of a smaller nanoparticle,

The dimer mode behaves as a large antenna, and at the same time it behaves as a small cavity, which is exactly what is needed for strong field enhancement as shown schematically on the right hand side of Figure 3a.

When the light with a resonance frequency ω = ω s = ω 0 1 − κ is incident onto the dimer, the amplitudes of LSP in two modes are

and the maximum field in the symmetric mode is

The enhancement occurs because for the supermode the antenna volume is determined primarily by the larger nanoparticls, while the effective cavity volume by the small nanoparticle. The additional enhancement factor is

From this expression it follows that F _s can become arbitrary large as K increases. However, there is also the asymmetric mode, and in that mode the dipole of small nanoparticle is directed against the one excited in the symmetric mode, i.e.

Substituting (31) we obtain for the added enhancement in dimer,

In Figure 4a the total dimer enhancement F d = | F 1 F 2 | is plotted for two different Q-factor for gold Q=10 and silver Q=20 (also shown as dashed liens is the enhancement by a single nanoparticle | F 1 | ) As K increases, i.e. the volume of smaller nanoparticle decreases, the coupling decreases as κ ∼ K − 1 / 2 . As a result, F _a approaches F _s , hence one simultaneously excites both modes, and the enhancement saturates. The saturation sets in when Q κ ∼ 1 or K ∼ ( Q A ) 2 . For K > > 1

Figure 4:

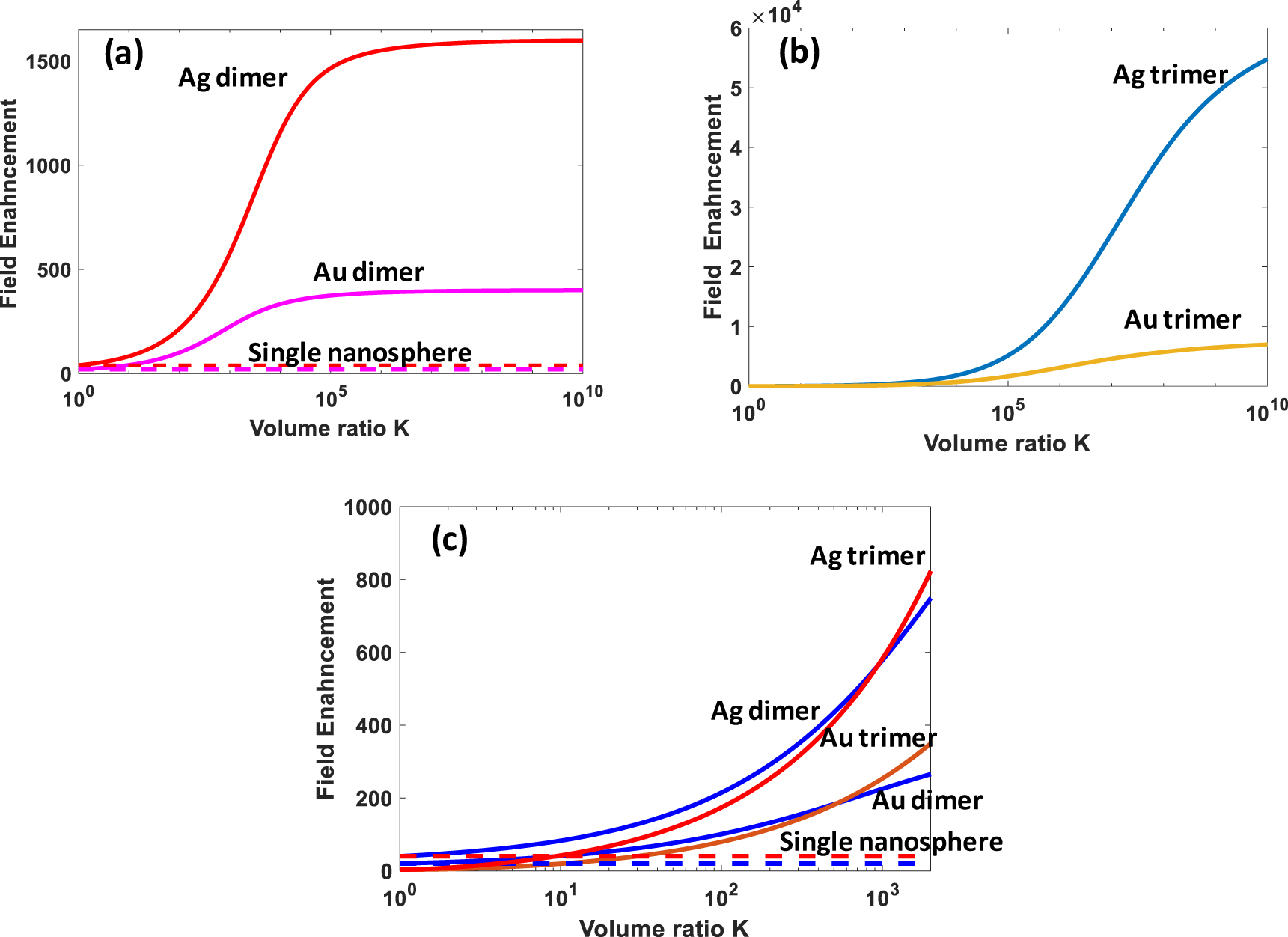
Field enhancement in (a) plasmonic dimers, (b) plasmonic trimers, and (c) zoomed in practical region where enhancement is not impeded by Landau damping.

The total enhancement in dimer is therefore F d = | F 1 | 2 = Q 2 A 2 . Thus in the dimer the field enhancement can be thought to occur in two steps – first large nanoparticle gets excited and then its field excites the smaller one, each step has the same enhancement, QA. One can see now that in order to provide larger enhancement one must increase coupling (i.e. reduce ratio K) while keeping smaller nanoparticle volume small (i.e. having a high K). Obviously this cannot be accomplished in a dimer and one should consider moving on to more complex schemes.

5 Extension of coupled mode theory to three and more nanoparticles

The task of reducing the volume of smallest nanoparticle while keeping coupling strong can be accomplished by inserting an intermediary nanoparticle between the “antenna” V ₁ and “cavity” V 3 = V 1 / K with its volume V 2 = ( V 1 V 3 ) 1 / 2 = K − 1 / 2 as shown in Figure 3c. The coupled equations are

where according to (31)

For large K coupling κ ≈ K − 1 / 4 i.e. it is stronger than in the dimer. The three super-modes are

with resonance frequencies ω ₀, ω 0 − 2 κ , and ω 0 + 2 κ respectively and polarizabilities

The effective volumes as antennas for three modes, shown in Figure 3b are

Once again, the effective volume as an antenna (i.e. effective dipole) is determined by the largest nanoparticle hence the trimer can effectively couple to the free space. Operating at resonance frequency we immediately obtain

The effective volumes as cavities are

These volumes, determined by the smallest nanoparticle are small which is advantageous for coupling to the angstrom-size quantum oscillators. The maximum fields on resonance are

Thus additional field enhancement with trimer antenna is therefore

In Figure 4b the total dimer enhancement F t = | F 1 F 3 | are plotted for two different Q-factor for gold and silver For K > > 1 the added enhancement saturates at

and the total trimer field enhancement is F t = ( Q A ) 3 . It is not difficult to make a conjecture that by going to larger number of nanoparticle in a chain, an even larger enhancement ( Q A ) N can be attained. But the question is how larger can K be, i.e. how large can be V ₁ and how small can be V _N ? Maximum size of V ₁ is on the scale of λ / 10 − λ / 5 , i.e. he point where radiative damping reduces Q. One assumes it is anywhere between ( 50 nm ) 3 and ( 100 nm ) 3 , minimum size of V _N is between ( 5 nm ) 3 and ( 10 nm ) 3 , i.e. where Landau damping becomes the dominant damping mechanism reducing Q. Therefore, maximum K is only about 2 × 10³. Then, as can be seen in Figure 4c for spherical nanoparticle there is very little difference in the additional enhancement between dimer and trimer and also for Au and Ag. The additional enhancement is anywhere between the factor of 12–15 for dimer and 18–20 for trimer. This perhaps explains why trimers and more complex structures have not found many applications as slightly improved enhancement does not justify increased complexity. At any rate, the total field enhancement in dimer or trimer reaches about 300 for Au and 800 for Ag which enhances the absorption by as much as 10⁵ for Au and 5 × 10⁵ for Ag. It is important to note here that Mark Stockman was one of the first to note that Landau damping can limit degree of enhancement attainable in plasmonics [33].

6 Effective volume for quantum absorber/emitter and its use for quantifying absorption and emission enhancement

As has been mentioned above, it had been shown that quantum entity, emitter, or absorber can be represented by a circuit model with L, C, and R is series and characterized by impedance Z(ω). Here and alternative is presented. This alternative consists of representing quantum emitter/absorber as a classical dipole oscillator, characterized (in addition to resonance frequency ω ₁₂ and damping rate γ _a ) by the effective volume V _eff,a . This model can then be applied to describe absorption and emission by quantum oscillator as well as its coupling to the antennas. The energy of a quantum oscillator and its dipole are related as

Therefore, we can introduce the “amplitude” of the atomic motion as a square root of its energy, or, essentially, a classical analogue of annihilation operator.

Substituting it into Eq. (1) one obtains

and the differential equation for a _a is

where

If we now compare (59) with (27) we can even introduce the effective volume for the quantum oscillator

Since in the visible/near IR region the dipole for an allowed transition r 12 ∼ 1 Å , the effective volume is on the scale of about 10 nm³ and less so for the weaker transitions. Thus, two level system embedded in the dielectric can be treated in the same way as any other oscillator, described by its effective volume, polarizability, resonant frequency, and damping rate.

Now, the coupling of energy into a quantum absorber using a nanoantenna consisting of N nanospheres can be approached as coupling into a hybrid supermode with N+1 entities – N nanospheres and a quantum oscillator. Such a hybrid mode has effective dipole that exceeds r ₁₂ by many orders of magnitude. In Figure 5a a dimer antenna with nanospheres of volumes V ₁ and V ₂ coupled into the quantum absorber with effective volume V _eff,a is represented as a hybrid trimer. If the absorber is resonant with the antenna, ω ₁₂=ω ₀, one can see that the optimum coupling will be achieved when V 2 , eff = ( V 1 , eff V eff , a ) 1 / 2 . The coupling coefficient, according to (46) is κ = A K 1 / 4 ( 1 + K 1 / 6 ) − 3 where K = V 1 , eff / V a , eff and by performing all the steps outlined in a previous section one obtains for the amplitude of quantum oscillator a a = F t α a E ext . Introducing the intensity of the incoming light I in = E ext 2 ϵ d 1 / 2 / η 0 , the rate of energy transfer to the atomic oscillator is

Figure 5:

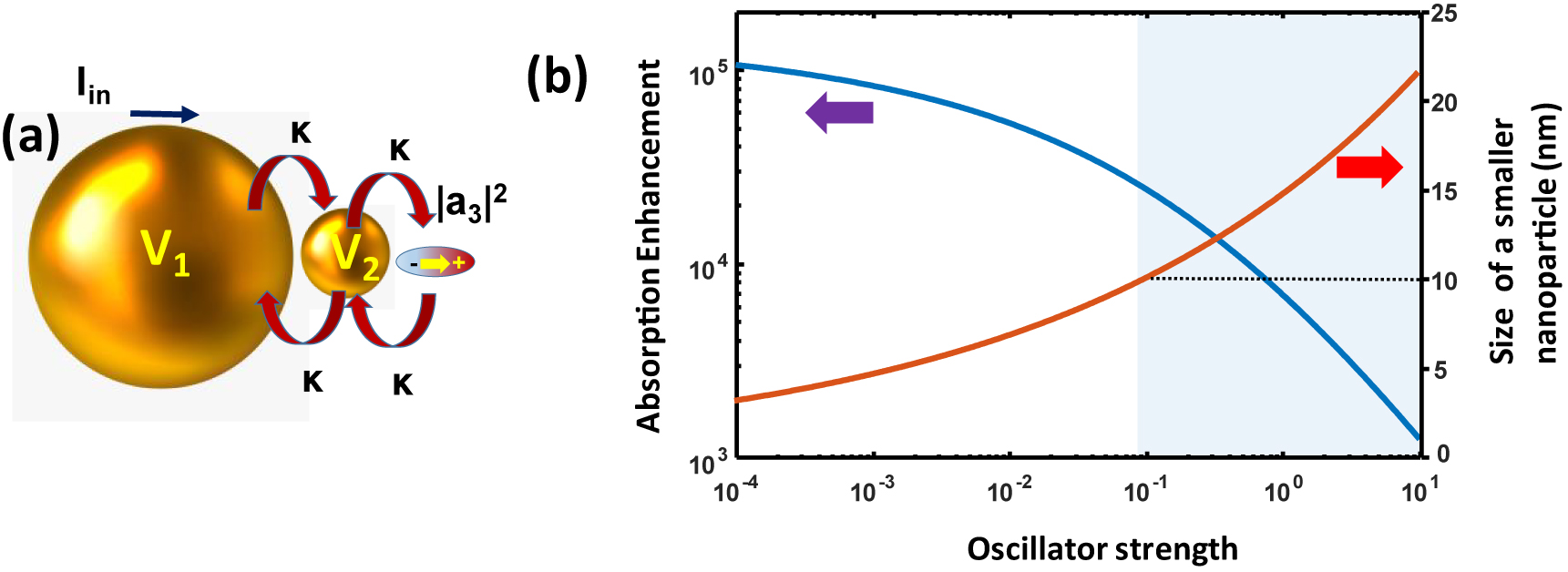
(a) Nanofocusing in a hybrid trimer consisting of a plasmonic dimer and quantum oscillator. (b) Enhancement of absorption. Shaded region represents a practical range of enhancement not impeded by excessive Landau damping.

In the absence of nanoantenna the absorption cross section is

Therefore, the absorption cross-section with dipole antenna gets enhanced

Note that here the decay rates of atomic oscillator and LSP has been assumed to be equal. If they are not equal, one has to introduce the weighted average γ which will change the results but not all that significantly unless γ a > γ , which is highly unlikely given broad linewidths of LSP modes. The question is how large can the ratio K be? Assuming that V 1 , eff ∼ ( 100 nm ) 3 and expressing V eff , a ≈ 10 nm 3 × f 12 using (60) we obtain K max ∼ 10 5 / f 12 . The enhancement is plotted versus oscillator strength in Figure 5. Note that oscillator strength may exceed unity due to small effective mass as is the case in semiconductor quantum dots [34]. As it is true for the entire field of plasmonics, the enhancement is the strongest for the weak absorbers with smaller oscillator strength [35]. Unfortunately, once again, the largest enhancements are not attainable since the required size of the smaller nanoparticle V 2 1 / 3 , also shown in Figure 5b becomes so small (less than 10 nm) that Landau damping reduces Q-factor dramatically. As a result, the largest enhancement for Au is on the scale of 2.5 × 10⁴ and for Ag is should be 4 times as large. The enhancement (63) represent the ratio of the squares of effective dipole moments of a quantum absorber/emitter and the hybrid mode. Obviously, the enhancement of the rate of spontaneous emission will be similar, as explained in [21]. The enhancement of Raman scattering the can reach 10¹⁰. In the end, whether it is efficiency of absorption or emission using adiabatic concentration, the hard limit is set by Landau damping that requires the smallest nanoparticle (or tip of waveguide) to be at least 5–10 nm to avoid excessive loss.

7 Conclusions

In this work Mark Stockman’s contributions to just one area of photonics has been highlighted. Thanks to him, the idea of nanofocusing took root in the community, and plenty of theoretical and experimental works have followed. Perhaps inevitably, the original idea often became compromised by excessive hype and unsustainable claims, but the core of Mark predictions has been indeed confirmed. Plasmonics undeniably offers unique chance to confine light into minuscule volumes and achieve very strong fields which can be used for probing the matter on a nanoscale [36], if not for more exotic applications in photonic integrated circuits and light sources. Excessive loss due to Landau damping does prevent us from fully realizing the nanofocusing potential, but it Is not entirely impossible that the issue of loss will be addressed in the future. Before I conclude, I should note that Mark Stockman himself never oversold his ideas and habitually offered a sober and critical assessment of trendy topics, be that negative refraction [37, 38], epsilon near zero materials [39], spoof plasmons [40] and other. His critical eye and sober mind will be just as missed as his unabashed enthusiasm for science, never ending quest for discovery, and his zest for life which he preserved all the way to the end.