Abstract
Medical device technology develops rapidly, and the life cycle of a medical device is much shorter than drugs. It is necessary to evaluate the safety and effectiveness of a medical device in a timely manner to keep up with technology flux. Bayesian methods provides an efficient approach to addressing this challenge. In this article, we review the characteristics of the Bayesian approach and some Bayesian designs that were commonly used in medical device regulatory setting, including Bayesian adaptive design, Bayesian diagnostic design, Bayesian multiregional design, and Bayesian label expansion study. We illustrate these designs with medical devices approved by the US Food and Drug Administration (FDA). We also review several innovative Bayesian information borrowing methods, and briefly discuss the challenges and future directions of the Bayesian application in medical device trials. Our objective is to promote the use of the Bayesian approach to accelerate the development of innovative medical devices and their accessibility to patients for effective disease diagnoses and treatments.
Introduction
The Bayesian approach and the frequentist approach are two main methods used in clinical study design and data analysis [1]. The frequentist approach has been more commonly used in regulatory setting because of its long history and better understood statistical properties [2]. The Bayesian approach provides an alternative to the frequentist approach, which combines prior distribution with the newly observed data through the likelihood function to obtain the posterior distribution for the parameter of interest (e.g., the efficacy or safety endpoint) [3].
With the rapid development of innovative medical products, there is an increasing interest in efficient safety and effectiveness evaluation. Many innovative methods for design and analysis in medical product clinical studies have been proposed. Some of them are encouraged by the US Food and Drug Administration (FDA), for example master protocol trials [4] and complex innovative trial designs [5]. These innovative methods often prefer using the Bayesian approach to the frequentist approach [6], owing to its flexibility and ability to borrow existing information to improve the efficiency of clinical studies. In addition, compared to the frequentist approach (e.g., p-value and confidence interval), the Bayesian approach has better interpretation because it provides intuitive probability statements on the parameter of interest, e.g., what is the probability that the treatment effect reaches the clinically meaningful values [7]. Consequently, using the Bayesian approach to improve the efficiency and accuracy of the evaluation of innovative medical products has been a topic of great interest. At present, there have been more than 200 clinical trials using the Bayesian approach for study design and analysis at the University of Texas MD Anderson Cancer Center [8].
Bayesian methods are particularly attractive for evaluating medical device clinical studies. Medical device technology develops rapidly, and the life cycle of a medical device is much shorter than drugs. It is necessary to evaluate the safety and effectiveness of a medical device in a timely manner to keep up with technology flux. Moreover, since medical devices typically evolve from previous versions with a similar action mechanism, clinical data of early versions could provide valuable experience as prior information borrowing to a new version device. In February 2010, FDA issued a guidance for the use of Bayesian statistics in medical device clinical trials [9]. There have been 47 medical devices approved by FDA that relied on the Bayesian design or Bayesian statistics (Table 1). However, the Bayesian approach have been under-utilized in other countries, such as China, Japan, etc.
Medical devices approved by FDA involving the Bayesian approach, 1998–2022.
| Number | Medical devices | PMA number | Subject | Approved date | Description of the Bayesian approach |
|---|---|---|---|---|---|
| 1 [39] | Multi-frequency Impedance Breast Scanner | P970033 | Radiology | 1999.4.16 | Bayesian multinomial-logistic model to combine three clinical study results |
| 2 [40] | Intervertebral Body Fusion Device | P970015 | Orthopedic | 1999.5.14 | Bayesian predictive probabilities |
| 3 [41] | Cervical Interbody Fusion System Instrumentation | P980048 | Orthopedic | 2001.4.20 | Bayesian success criterion and Bayesian credible intervals |
| 4 [42] | Implanted Mechanical/hydraulic Urinary Continence Device | P000053 | Gastroenterology/Urology | 2001.6.14 | Bayesian hierarchical model |
| 5 [43] | Interactive Wound Dressing | P000036 | General & Plastic Surgery | 2001.9.28 | Bayesian interim analysis |
| 6 [44] | Intervertebral Cervical Cage | P000028 | Orthopedic | 2002.6.13 | Bayesian credible intervals |
| 7 [45] | Collagen Scaffold with Metal Prosthesis | P000058 | Orthopedic | 2002.7.2 | Bayesian predictive probabilities |
| 8 [46] | Contraceptive Tubal occlusion device and delivery System | P020014 | Obstetrics/Gynecology | 2002.11.4 | The effectiveness results from the two studies were combined using Bayesian statistics |
| 9 [47] | Drug-Eluting Coronary Stent System | P020026 | Cardiovascular | 2003.4.24 | Bayesian statistics |
| 10 [48] | Replacement Heart Valve | P040021 | Cardiovascular | 2005.8.5 | Bayesian approach deal with missing data |
| 11 [49] | Artificial Cervical Disc System | P060018 | Orthopedic | 2007.7.16 | Bayesian design and Bayesian predictive probabilities |
| 12 [50] | Replacement Heart Valve | P040021/S004 | Cardiovascular | 2007.11.15 | Borrowing historical data and Bayesian hierarchical model |
| 13 [51] | Iliac Stent | P080007 | Cardiovascular | 2008.12.4 | Bayesian non-informative prior |
| 14 [29] | Irrigated Diagnostic/Ablation Catheter and Accessories | P030031 | Cardiovascular | 2009.2.6 | Bayesian predictive probabilities and posterior probability |
| 15 [52] | Artificial Cervical Disc | P060023 | Orthopedic | 2009.5.12 | Bayesian non-informative prior |
| 16 [53] | Bronchial Thermoplasty System | P080032 | Anesthesiology | 2010.4.27 | Bayesian superiority design |
| 17 [54] | Intracranial Aneurysm Flow Diverter | P100018 | Neurology | 2011.4.6 | Bayesian non-informative prior and Bayesian credible intervals |
| 18 [27] | Electrosurgical Device | P100046 | Cardiovascular | 2011.12.15 | Bayesian adaptive design with interim monitoring, posterior probabilities, and credible intervals |
| 19 [55] | Artificial Cervical Disc | P100003 | Orthopedic | 2012.9.28 | Bayesian predictive probabilities and Bayesian credible intervals |
| 20 [56] | Interlaminar Stabilization Device | P110008 | Orthopedic | 2012.10.17 | Bayesian interim analysis, Bayesian non-informative prior, and Bayesian credible intervals |
| 21 [57] | Endovascular Graft | P040043 | Cardiovascular | 2013.9.10 | Bayesian adaptive design |
| 22 [58] | Cardiac Resynchronization Therapy Pacemaker | P010015 | Cardiovascular | 2014.4.10 | Bayesian adaptive design |
| 23 [59] | Cardiac Resynchronization Therapy Defibrillator | P010031 | Cardiovascular | 2014.4.10 | Bayesian adaptive design |
| 24 [60] | Artificial Cervical Disc | P090029 | Orthopedic | 2014.7.24 | Bayesian logistic model and Bayesian linear model |
| 25 [26] | Prosthesis, Spinous Process Spacer/Plate | P140004 | Orthopedic | 2015.5.20 | Bayesian adaptive design |
| 26 [61] | Left Atrial Appendage Closure System | P130013 | Cardiovascular | 2015.3.13 | Bayesian adaptive design |
| 27 [62] | Hyaluronic Acid, Intra-articular | P150010 | Orthopedic | 2015.8.28 | Bayesian regression analysis |
| 28 [63] | Sodium Hyaluronate for Injection | P140005 | Orthopedic | 2015.9.2 | Bayesian longitudinal analysis |
| 29 [20] | Drug Eluting Coronary Stent System | P070015 | Cardiovascular | 2015.9.23 | Bayesian hierarchical model |
| 30 [64] | Drug Eluting Coronary Stent System | P110019 | Cardiovascular | 2015.9.23 | Bayesian meta-analysis |
| 31 [65] | Reherniation Reduction device | P160050 | Orthopedic | 2016.2.19 | Bayesian superiority design |
| 32 [66] | Artificial Cervical Disc | P090029 | Orthopedic | 2016.7.7 | Bayesian hierarchical model, Bayesian predictive probabilities, and Bayesian credible intervals |
| 33 [67] | Somatic or Germline Variant Detection System | P170019 | Pathology | 2016.12.19 | Bayesian hierarchical model |
| 34 [38] | Autonomic Nerve Stimulator for Epilepsy | P970003 | Neurology | 2017.6.23 | Bayesian hierarchical model |
| 35 [68] | Replacement Heart Valve | P130021 | Cardiovascular | 2017.7.10 | Bayesian adaptive design |
| 36 [69] | Somatic or Germline Variant Detection System | P160018 | Pathology | 2017.11.30 | Bayesian hierarchical model |
| 37 [25] | Acute Coronary Syndrome Event Detector | P150009 | Cardiovascular | 2018.4.9 | Bayesian adaptive design and Bayesian predictive probabilities |
| 38 [70] | Intracranial Neurovascular Stent | P170013 | Neurology | 2018.5.30 | Bayesian posterior mean, posterior probability, and credible intervals |
| 39 [71] | Endobronchial Valve | P180007 | Anesthesiology | 2018.12.3 | Bayesian superiority design and Bayesian multiple imputation for missing data |
| 40 [72] | Coronary Stent | P170030 | Cardiovascular | 2019.2.22 | Bayesian non-inferiority design and Bayesian hierarchical model |
| 41 [13] | Implantable Impulse Generator | P180036 | Cardiovascular | 2019.5.21 | Borrowing historical data |
| 42 [73] | Super Saturated Oxygen Therapy | P170027 | Cardiovascular | 2019.4.2 | Borrowing historical data and Bayesian hierarchical model |
| 43 [74] | Carotid Sinus Stimulator | P180050 | Cardiovascular | 2019.8.16 | Bayesian adaptive design |
| 44 [75] | Lidocaine/Epinephrine Iontophoresis and Automated Tympanostomy Tube Insertion System | P190016 | Ear Nose & Throat | 2019.11.25 | Bayesian hierarchical model |
| 45 [76] | Intracranial Aneurysm Flow Diverter | P180027 | Neurology | 2019.12.16 | Bayesian analysis, Bayesian non-informative prior, and Bayesian credible intervals |
| 46 [77] | Drug-Eluting Peripheral Transluminal Angioplasty Catheter | P190019 | Cardiovascular | 2020.10.30 | Bayesian predictive model |
| 47 [78] | Implant, resorbable, for articular osteochondral repair | P210034 | Orthopedic | 2022.3.29 | Bayesian analysis |
-
Based on the Summaries of Safety and Effectiveness (SSEDs) of the Premarket Approvals (PMA) Database.
In addition, large-scale real-world clinical data and high-quality completed medical data has been accumulated with the development of digital collection and storage technology in the era of modern clinical studies [10]. Numerous data sources have been established including electronic health records (EHRs), claims and billing data, product and disease registries, and data gathered through personal devices and health applications. These data sources broaden the scope for Bayesian information borrowing, bringing both opportunities and challenges to medical device clinical studies. In recent years, various types of innovative methods for information borrowing have been proposed [11]. One type is concurrent borrowing, which borrows information adaptively across multiple parallel arms. Another type is nonconcurrent borrowing, which borrows historical information from external data sources.
In this article, we summarize the characteristics of Bayesian methods, and review Bayesian designs that are commonly used in medical device regulatory setting, including Bayesian adaptive design, Bayesian diagnostic design, Bayesian multiregional design, and Bayesian label expansion study. Furthermore, we review several innovative Bayesian information borrowing methods in the era of modern clinical studies and provide guidance on choosing appropriate methods based on their characteristics (e.g., data exchangeability, the type of outcomes, the number of arms/historical studies). Our objective is to promote the use of the Bayesian approach to accelerate the development of innovative medical devices and their accessibility to patients.
Characteristics of the Bayesian approach
Borrowing information
One of the most prominent characteristics for the Bayesian approach is its ability to incorporate prior information through the specification of prior distribution. If prior information is appropriately used, the Bayesian approach can substantially reduce the sample size and study duration. Medical devices develop more rapidly than drugs. The prior information comes naturally from the study of previous versions of the device with similar action mechanisms or the study accomplished in other regions. Borrowing information have been particularly successful to assess effectiveness and safety of cardiovascular devices [12], owing to their fast update speed. There have been 3 cardiovascular devices approved by FDA through the Bayesian information borrowing methods (Table 1). For example, to assess the primary effectiveness endpoint (i.e., the change in peak V02 at 24 weeks from baseline) of an implantable impulse generator [13], a Bayesian model was employed to construct prior distribution obtained from a previous study (FIX-HF-5) 229 patient subgroup. The posterior probabilities were >0.91, meaning that there is a probability of 91 % that the device group was superior to the control group. In late section, we will review some commonly used Bayesian information-borrowing methods.
The likelihood principle and predictive distribution
The likelihood principle is not only the foundation of the frequentist approach but also the core of the Bayesian approach. This principle says that all information about the endpoint obtained from a clinical study is included in the likelihood function [14, 15]. Therefore, the posterior distribution, obtained by combining the prior distribution with the likelihood, should be the basis for all Bayesian inferences about the parameters.
The posterior distribution renders the Bayesian approach great flexibility in study design. Under the Bayesian paradigm, the predictive distribution of the future observations can be generated by first sampling model parameters from their posterior distribution and then, conditional on the parameters, sampling the future observations from the likelihood function. In contrast, for the frequentist approach, the probability of the future observations can only be obtained by fixing the model parameters, which ignores the uncertainty associated with the parameter estimation. Posterior and predictive distributions have been widely used in Bayesian clinical studies, such as making go/no-go decisions, and using covariates to predict clinical outcomes [16, 17]. For example, the Bayesian optimal phase 2 (BOP2) design [18], which makes go/no-go decision based on posterior probabilities, have been used in over 100 on-going clinical trials [19]. There have been 16 medical devices approved by FDA through the Bayesian predictive distribution (Table 1). For example, a Bayesian predictive modeling was used to estimate the 3-year mortality rate and compared to a performance goal (PG) of 12.9 % in a Drug-eluting peripheral transluminal angioplasty catheter clinical study [20].
Exchangeability
The Bayesian approach often assumes that participants within a study are exchangeable, and the studies are also exchangeable with each other [21]. If the probability of observing any set of endpoints within these participants, subgroups, or studies is invariant to any reordering, these participants, subgroups, or studies are considered exchangeable. In this case, the data from these studies could be directly combined. However, this is often not the case in practice. Observations from different studies are often not exchangeable due to different regions, different centers, or different researchers, even though the protocols seem similar with each other. Moreover, when the new version of a device is expected to be superior to previous versions, the current study is typically not exchangeable with previous studies. Therefore, it is necessary to consider conducting participants regularization, choosing appropriate borrowing information methods, and quantifying the amount of borrowing. In addition, the current study and previous studies may not be exchangeable due to differences in baseline covariates, although they might be exchangeable after conditioning on the covariates [22].
Bayesian designs in medical devices
Bayesian adaptive design
The FDA guidance discussed two major approaches: one is borrowing information from previous studies, which is introduced in the section of “Borrowing information”; another is to use Bayesian adaptive design [9]. Bayesian adaptive study is usually designed with no prior information but rather relying on accumulating data collected within the current study to potentially make preplanned changes during the course of the study. For example, during a Bayesian adaptive study, the sample size could be modified according to accumulating data while maintaining the targeted power, which may result in shorter study duration and smaller sample size [23]. This sample size re-estimation can be based on the predictive distribution, accounting for not only the subjects already enrolled in the trial, but also the subject yet to be recruited. Moreover, Bayesian adaptive design could construct likelihood predictive models to predict endpoints at later time points (unobserved outcomes) based on the information obtained at earlier follow-up time points (observed outcomes). The primary outcomes using time-dependent intermediate ones are usually modeled by piecewise exponentials [24].
Bayesian adaptive design is particularly suitable for cardiovascular and orthopedic device assessment [25], [26], [27], [28]. These kinds of medical device usually have a slow accrual rate relative to the patient follow-up so that is very expensive to conduct. Therefore, there are adequate time to predict and make adaptations based on the several interim follow-up measurements to make effort to shorten the study duration and reduce the sample size. There have been 9 medical devices approved by FDA through the Bayesian adaptive design (Table 1). The safety and effectiveness assessment of an electrosurgical ablation system was a typical Bayesian adaptive design, which fully used the Bayesian approach to evaluate primary outcomes, including interim analysis, sample size re-estimation, and final decision [27]. The minimum total sample size was 50 and the maximum was 100. At each interim analysis, the predictive probabilities of meeting the primary safety and effectiveness endpoint were calculated using information from the subjects with known outcomes, in combination with a beta-binomial distribution for modeling the transition from either baseline or 3-month outcomes to the 6-month outcomes. Whether to stop patient accrual, stop the study for futility, or continue enrolling subjects was decided by the predictive probabilities.
Bayesian diagnostic design
The Bayesian approach could also be applied in the assessment of medical diagnostic devices [29]. Under the framework of Bayesian diagnostic design, the disease prevalence is considered as prior probability (pre-test probability), and the predictive value of the test is considered as posterior probability (post-test probability) [30]. The probability of the positive test results in truly positive subjects is translated to sensitivity. Similarly, the probability of the negative test results in truly negative subjects is translated to specificity. Furthermore, the positive predictive values (PPV) and negative predictive values (NPV) of the device could be defined by prevalence, sensitivity, and specificity. Indeed, Bayesian diagnostic design is still based on the theory of using prior distribution to predict posterior distribution.
Bayesian multiregional design
The International Conference on Harmonization (ICH) Guideline E5 (1998) proposed multiregional clinical trial (MRCT) design for accelerating the development of innovative drugs and medical devices [31]. MRCT design has advantages of faster enrollment rate, less cost, and providing an opportunity of simultaneous multiregional registration. However, the overall effect may not be consistent from region to region due to the variability among regions. It is difficult to conduct statistical evaluation of the safety and effectiveness for the intended population, especially the region by treatment interaction without statistical significance [32, 33]. Compared to drugs, medical devices tend to be with smaller sample size. MRCT of medical devices are often planned with sufficient subjects to indicate an overall effect in the primary endpoint, thus there may not be adequate power to indicate a statistically significant result at the usual significance level within a specific region. The above problems in effect statistical evaluation could not be solved well by the frequentist approach.
Bayesian hierarchical model could borrow information across different layers, which is appropriate to assess the overall and regional treatment effects and determine the optimal sample size in multiregional medical device study. Chen evaluated regional treatment effects in a multiregional trial through a Bayesian approach [34]. The overall treatment effect was used as prior and conditioned on the observed regional treatment effect to construct the posterior distribution of the regional treatment effect. Furthermore, Bayman discussed the statistical operation and sample size for multiregional clinical studies under a Bayesian hierarchical model [35]. Compared to the frequentist approach (i.e., conventional subgroup analysis), the use of Bayesian hierarchical model in multiregional studies is more powerful because of its ability of borrowing information across different regions, especially existing regional variability. However, the larger the variation the less is the borrowing of information across regions [36]. In addition, the possible underlying caused should be analyzed carefully, when the significant differences exist across regions. The particular regions with large heterogeneity might be excluded from the total analysis.
Bayesian label expansion study
There is a growing interest in leveraging real-world data (RWD) in medical product development. Real-world evidence (RWE) has been used for registrations since the FDA issued the guidance about using real-world evidence in regulatory decisions for medical devices [37]. One of the applications of RWE is to conduct label expansion studies. The Bayesian approach was usually used in these studies benefiting from its ability of borrowing safety information from registered indication to the new indication. That is to say, safety data from real-world use of the device for the approved indication is used to build a prior distribution for the safety assessment of the new indication. There have been several successful experiences in medical device label expansion studies by the Bayesian approach [20, 38]. For example, a drug-eluting coronary stent to the new indications of diabetes patients borrowing information from four real-world databases through a Bayesian hierarchical model [20]. With the rapid speed of accumulating RWD, Bayesian label expansion studies will be more and more widely used in the future registration.
Bayesian FDA submission
Medical devices approved by FDA involving the Bayesian approach from 1998 to 2022 is shown in Table 1. The list is based on the Summaries of Safety and Effectiveness (SSEDs) of the Premarket Approvals (PMA) Database. In general, there have been 47 medical devices approved by FDA which relied on the Bayesian design or Bayesian statistics. Wherein 15 medical devices were approved during 1998–2010. An additional 32 medical devices were approved since FDA published the guidance about the use of Bayesian statistics in medical device clinical trials in 2010. There were 19 (40.4 %) medical devices belonging to cardiovascular and 15 (31.9 %) medical devices belonging to orthopedic because the Bayesian approach could make these medical devices with slow accrual rates and long follow-up much more flexible. Bayesian adaptive study (9, 19.1 %) was the most commonly used designs in medical device clinical trials.
Bayesian information borrowing methods in the era of modern clinical studies
With the development of digital collection and storage technology in the era of modern clinical studies, abundant data sources have been formed and broaden the scope for information borrowing in the Bayesian approach [10]. The exchangeabilities among patients and studies are the basic principle of Bayesian information borrowing. However, the heterogeneity among the current study and different data sources could not be avoided. In recent years, many innovative information borrowing methods have been derived from traditional methods to make effort to deal with the heterogeneity. We summarize these information borrowing methods according to the concurrent borrowing strategy and nonconcurrent borrowing strategy (Table 2).
Descriptions of commonly used Bayesian information borrowing methods.
| Information borrowing | Methods | Features |
|---|---|---|
| Concurrent borrowing | ||
| (1) BHM and its extensions | ||
| BHM | Variance in hierarchical model reflects heterogeneity and estimate it using fully Bayesian method | |
| CBHM | Variance is a function of heterogeneity measurement | |
| BaCIS | Dichotomous cluster between arms and borrow information within each cluster | |
| BCHM | Nonparametric clustering method is used to dynamically determine the number of clusters | |
| CLBHM | Treatment arms are clustered into active and inactive clusters based on the posterior probability of the treatment effect, and then BHM is applied to each cluster for information borrowing | |
| (2) MEMs | ||
| MEMs | Specify all possible pairwise exchangeability models among arms by a symmetric matrix and weight above models | |
| Nonconcurrent borrowing | ||
| (1) PP and its extensions | ||
| PP | Downweigh the historical trial by a prespecified power α | |
| MPP | α follows a vague prior and is estimated by combined data | |
| CPP | α is a function of heterogeneity measurement | |
| (2) CP | ||
| CP | Parameter in the current trial centers around the historical trial | |
| (3) Elastic prior | ||
| Elastic prior | Inflating variance uses an elastic function | |
| (4) MAP and its extensions | ||
| MAP | Parameters in historical trials and the current trial come from the same normal distribution with variance reflecting heterogeneity | |
| RMAP | A hybrid prior is constructed by weighted non-informative prior and MAP | |
| (5) SAM | ||
| SAM | The mixing weight is determined by likelihood ratio test statistics to favor the informative (non-informative) prior component | |
| (6) MEMs | ||
| MEMs | Specify all possible pairwise exchangeability models among trials by a vector and weight above models | |
| (7) PS-integrated priors | ||
| PS-PP | Trimming and stratification by PS; α is specified by a similarity measure between PS distributions of the patients in the current study and the external study | |
| PS-MAP | Trimming and stratification by PS; ESS is adjusted based on a similarity measure between PS distributions of the patients in the current study and the external study | |
| PS-RMAP | Trimming and stratification by PS; a hybrid prior is constructed by weighted non-informative prior and MAP | |
-
BHM, Bayesian hierarchical model; CBHM, calibrated Bayesian hierarchical model; CLBHM, clustered Bayesian hierarchical model; BaCIS, Bayesian hierarchical classification and information sharing; BCHM, Bayesian cluster hierarchical model; MEMs, multisource exchangeability models; PP, power prior; MPP, modified power prior; CPP, calibrated power prior; CP, commensurate power prior; MAP, meta-analytic-predictive prior; RMAP, robust meta-analytic-predictive prior; SAM, self-adapting mixture prior; PS, propensity score; PS-PP, propensity score-integrated power prior; PS-MAP, propensity score-integrated meta-analytic-predictive prior; ESS, effective sample size; PS-RMAP, propensity score-integrated robust meta-analytic-predictive prior.
Concurrent borrowing methods
Concurrent borrowing is applied in the master protocol. It is usually used in the study design with multiple parallel arms, such as basket trial design and platform trial design, to borrowing information within multiple sub studies. These arms are of equal importance and are analyzed simultaneously without a chronologic order. Bayesian hierarchical model (BHM) and its extensions and multisource exchangeability models (MEMs) are commonly used in concurrent borrowing. The I-SPY2 trial was designed as a platform trial that used a BHM to adaptively borrow information between running arms [79].
Bayesian hierarchical model and its extensions
Bayesian hierarchical model (BHM) was first proposed by Thall et al. [80], using variance in a hierarchical model to control the extent of borrowing (Table 2). BHM assumes the interested parameters in different trials comes form same normal distribution in which the variance τ reflects the heterogeneity. Specifically, let θ j denote the interested parameters from arm j, j=1, …, J.j follows the normal distribution with mean μ. A standard hierarchical model is:
HN(․) Denotes half-normal distribution. τ is the heterogeneity measurement parameter of different arms which controls the amount of borrowing from all J arms. Larger τ represents larger heterogeneity, so that the less information would be borrowed. The posterior distribution of τ is updated through the Bayesian approach.
The extensions of BHM focus on the specification of τ and which arms should be included into borrowing. Calibrated Bayesian hierarchical model (CBHM), Bayesian hierarchical classification and information sharing (BaCIS), Bayesian cluster hierarchical model (BCHM), and clustered Bayesian hierarchical model (CLBHM) are the four commonly used extensions of BHM (Table 2).
Calibrated Bayesian hierarchical model (CBHM) was first proposed by Chu et al. [81]. CBHM uses the heterogeneity measurement function to determine the extent of information borrowing, instead of specifying distribution of variance τ. Therefore, CBHM has the advantage of controlling type I error inflation, especially in the study with a small amount of arms.
Bayesian hierarchical classification and information sharing (BaCIS) was first proposed by Chen et al. [82]. Compared to CBHM, BaCIS clusters the arms adaptively with bipartition instead of calculating the heterogeneity across all arms directly. BaCIS uses a latent variable γ to divide arms into two categories: effective cluster and ineffective cluster. Then BHM is used to borrow information within each cluster.
Bayesian cluster hierarchical model (BCHM) was first proposed by Chen et al. [83]. Compared to BaCIS, BCHM uses non-parametric Dirichlet process G to adaptively and dynamically determine the numbers of clusters instead of fixed two clusters. Therefore, BCHM could bring information more flexibility.
Clustered Bayesian hierarchical model (CLBHM) was first proposed by Jiang et al. [84]. This approach first clusters treatment arms into active and inactive clusters based on the posterior probability of the treatment effect, and then apply BHM to each cluster for information borrowing. CLBHM is simple to implement, and often yields better and more robust performance than more complicated BaCIS and BCHM methods [84].
Multisource exchangeability models
Multisource exchangeability models (MEMs) were first proposed by Hobbs et al. in the scenario of multiple parallel arms existing [85], which specify all possible pairwise exchangeability models among arms by a symmetric matrix and weight above models (Table 2). The posterior estimate is the average of all models in which the weights are adaptively determined according to the similarity between arms.
Nonconcurrent borrowing methods
In the era of modern clinical studies, it has become a new trend to use large-scale real-world clinical data and high-quality completed medical data as external data into clinical studies. Nonconcurrent borrowing incorporates historical information from external data into the design of the current study, which offers the possibility of substantially reducing sample size. The paradigm of nonconcurrent borrowing only has one primary study, and others are considered as supplementary studies to provide historical information. Historical information is extracted to construct informative prior, which is further combined with the likelihood function of the current data to make inference and study decisions. Power prior (PP), commensurate prior (CP), elastic prior, meta-analytic-predictive prior (MAP), self-adaptive mixture (SAM) prior, and multisource exchangeability models (MEMs) are examples for nonconcurrent borrowing. In addition, the innovative propensity score (PS)-integrated priors have been proposed, which are considered as an efficient method to deal with the heterogeneity within patient-level covariates.
Power prior and its extensions
Power prior (PP) was first proposed by Ibrahim and Chen et al. [86]. Let H denote the historical data, θ denote the parameter of interest, and π(θ) denote a noninformative prior before accounting for H. PP is constructed by raising the likelihood function of historical data to the pre-specified power α (Table 2):
α lies between 0 and 1 and is fixed in the PP approach, which represents the extent of borrowing from historical data. α=1 represents complete borrowing (no discounting), and α=0 represents no borrowing (complete discounting). For example, the data of 686 subjects from an approved placental immunoassay diagnostic device for spontaneous preterm delivery was reanalyzed by leveraging 511 prior subjects in the PP approach [87, 88]. The posterior mean of α was 0.216 in which 111 prior subjects was borrowed. Finally, the posterior mean of sensitivity and specificity were similar but more precise than the estimates without borrowing.
In practice, it is usually difficult to pre-specify an appropriate value for α. Therefore, several extensions of PP have been proposed to determine the value for α. Modified power prior (MPP) and calibrated power prior (CPP) are the two commonly used extensions of PP (Table 2).
Modified power prior (MPP) was first proposed by Duan et al. [89]. Compared to PP, α in MPP is specified as a distribution instead of a specific value. The prior distribution π(α) is usually specified as non-informative prior or vague prior. Therefore, the posterior distribution is mainly estimated by combined data of historical study and current study. MPP belongs to a data-driven approach instead of subjective determination.
Calibrated power prior (CPP) was first proposed by Pan et al. [90]. Compared to PP, α in CPP is specified as a function which could measure the difference between historical study and current study. CPP could control type I error effectively, especially inter-study heterogeneity existing. Indeed, CPP also belongs to a data-driven approach which could dynamically borrow information based on similarity of historical data and current data.
Commensurate prior and its extensions
Commensurate prior (CP) was first proposed by Hobbs et al. [91]. Compared to PP, CP uses a commensurability parameter τ 2 to control the extent of borrowing from historical data instead of α (Table 2). The interested parameter θ of the current data is assumed following normal distribution and centered on the corresponding parameter θ 0 of historical data. Indeed, the commensurability parameter τ 2 is the variance which measures the heterogeneity between historical study and current study:
τ 2 is estimated by historical data and with smaller τ 2 indicating more extent of borrowing from historical data.
The extensions of CP could also incorporate dynamic borrowing, which is usually used to optimize the number of subjects randomized to a current control group by assessing the similarity of current control with the historical control [92].
Elastic prior
Elastic prior was first proposed by Jiang et al. [93]. In this approach, a full-information prior is first constructed as the posterior distribution of θ based on historical data H as follows,
The elastic prior is obtained by discounting π(θ|H), via inflating its variance, by an elastic function g(T) such that more/less information will be borrowed when the current data and historical data are similar/dissimilar. The similarity measure T can be t-test statistic for continuous endpoints and chi-squared test statistic for binary endpoints. Through the use of the elastic function, the elastic prior proactively controls the information borrowing based on the similarity between the current data and historical data, thus it achieves more accurate dynamic borrowing with better type I error control than PP and CP.
Meta-analytic-predictive prior and its extensions
Meta-analytic-predictive prior (MAP) was first proposed by Neuenschwandera et al. [94], which uses the basic idea of meta-analysis (Table 2). MAP assumes parameters from multiple historical studies and the current study following the same normal distribution:
τ 2 is the common variance of total studies, including all historical studies and the current study. Therefore, the posterior estimation is sensitive to the heterogeneity between studies when the number of historical studies is small.
Robust meta-analytic-predictive prior (RMAP) is the commonly used extension of MAP (Table 2), which was first proposed by Schmidli et al. [95]. Compared to MAP, RMAP leads into a non-informative prior to construct a hybrid prior, so that the posterior estimation is more robust. Indeed, RMAP is the weighted average of non-informative prior and MAP.
Self-adapting mixture prior
One major limitation of RMAP is that it requires the specification of the mixture weight to represent how likely that the historical data are exchangeable to the current study data, which unfortunately is typically unknown at the study design phase. Yang et al. proposed the self-adapting mixture (SAM) prior to address this issue [96], which takes the form a mixture of informative prior π(θ|H) and noninformative prior π(θ):
The SAM prior determines the mixing weight w using likelihood ratio test statistics to favor the informative (non-informative) prior component when there is little (substantial) evidence of prior-data conflict. Thus, it achieves more accurate and robust dynamic information borrowing than RMAP. SAM priors are data-driven, avoiding selection bias and potential data dredging inherent in fixed-weight mixture priors, thereby lowering the barrier for regulatory acceptance of borrowing external historical data. In addition, it seamlessly handles one or multiple external studies.
Multisource exchangeability models
Multisource exchangeability models (MEMs) were first proposed by Kaizer et al. in the scenario of multiple heterogeneous studies existing [21], which cold adaptively select homogeneous trials and borrow information form them among multiple studies. MEMs assume several exchangeable models between historical studies and the current study, and posterior distribution is estimated by model averaging.
Propensity score-integrated priors
In the era of modern clinical studies, the abundant data sources bring both opportunities and challenges. On the one hand, these data sources could support numerous clinical studies both as main data and external prior data to accelerate research progress. On the other hand, the heterogeneity within study-level and patient-level makes evidence synthetize and assess difficultly. The Bayesian approach has gained more attention due to its flexibility in calibrating uncertainty and handling data heterogeneity, and its inherent updating process. We have already summarized commonly used Bayesian information borrowing methods in the previous part of this paper. However, the above methods almost focus on dealing with the heterogeneity within study-level. In practice, patient-level covariates are different among different data sources leading to heterogeneity in efficacy, especially in nonconcurrent scenarios with a large time span. Propensity score (PS) is considered as a powerful tool in causal inference which is used as a balancing score in various ways to adjust for covariates [97]. PS methodology combines Bayesian priors has been proposed and become a new emerging external control borrowing strategy in a regulatory setting. Theoretically, PS-integrated prior could not only exert the advantages from various Bayesian models but also minimize bias from the external data. Examples in previous studies and FDA’s point of view indicated that PS-integrated prior have the potential to share information among data sources, evaluate the uncertainty of model, provide more reliable estimates in the scenarios of small sample size, and improve the efficiency of effect estimation compared with commonly used noncurrent borrowing methods [98], [99], [100], [101]. PS-integrated power prior (PS-PP), PS-integrated meta-analytic-predictive prior (PS-MAP), and PS-integrated robust meta-analytic-predictive prior (PS-RMAP) are the three innovative methods proposed under the framework of PS combining with Bayesian (Table 2).
PS-integrated power prior (PS-PP) was first proposed by Wang et al. for a single-arm study to leverage external RWD [102]. PS is used to pre-select a subset of RWD containing patients that are similar to those in the current study according to covariates, and to stratify the selected patients together with those in the current study into more homogeneous strata. This process is called “trimming”. Then the power prior is applied in which the power parameter α is specified for each strata derived from a similarity measure between PS distributions of the patients in the current study and the external data. Finally, stratum-specific posteriors are combined to obtain the posterior distribution for the parameters of interest. It is worth noting that the PS-PP approach could be applied in the two-stage outcome-free design in a regulatory setting. In the design stage, PS modeling, PS estimation, trimming, stratification, and the specification of α should be completed without outcome data in sight. In the analysis stage, the PS-PP is constructed and the posterior distribution is derived from the PS-PP and the outcome data in the current study. This two-stage outcome-free design ensures the validity and integrity of the clinical study [103].
The PS-PP approach has supported an approval of a new indication for an already approved cardiovascular device [102]. The data from the patient registries could be used as an external source of RWD in view of off-label usage for the targeted indication in the real world. The outcome is the incidence of adverse events (AE) θ in a year. If the posterior probability of θ<36 % was greater than 0.95, the study would be determined as successful. In the design stage, PS was calculated using the study indicator and 17 baseline covariates from 290 patients in the current study and 987 external patients. After trimming, 290 current patients and 941 external patients were included and divided into five PS strata. The similarity between current patients and external patients in each strata was evaluated through the overlapping of their PS distribution. In the analysis stage, the posterior distribution was derived combining the outcome of the current study. The posterior probability of θ<36 % is 96.9 %, which indicated meeting the success criterion.
Furthermore, Lu et al. extended the PS-PP approach to augment the control arm by incorporating multiple external data sources instead of single-arm study design [104]. In addition, Liu et al. proposed the PS-integrated meta-analytic-predictive prior (PS-MAP) approach to deal with large number of external data sources borrowing [105], which has the similar process with the PS-PP approach. Compared to PS-PP, the similarity measure between PS distributions of the current patients and external patients dynamically adjusts the prior effective sample size (ESS) in PS-MAP instead of the power α. However, the PS-PP and PS-MAP approach mainly deal with the heterogeneity between the current study and the external data sources. The heterogeneity between different external data sources is ignored. Zhu et al. used PS to stratify within each data sources instead of stratifying within combined data in the PS-PP and PS-MAP approach, and added non-informative prior into MAP to establish the PS-integrated robust meta-analytic-predictive prior (PS-RMAP) approach [106]. Simulation assessments indicated that the PS-RMAP approach was more efficient and less biased than the currently available information borrowing methods.
Application scenarios of information borrowing methods
Application scenarios of information borrowing methods have been the hot topic discussed by researchers all over the world. The recommendation for application scenarios on borrowing information methods are shown in Figure 1.
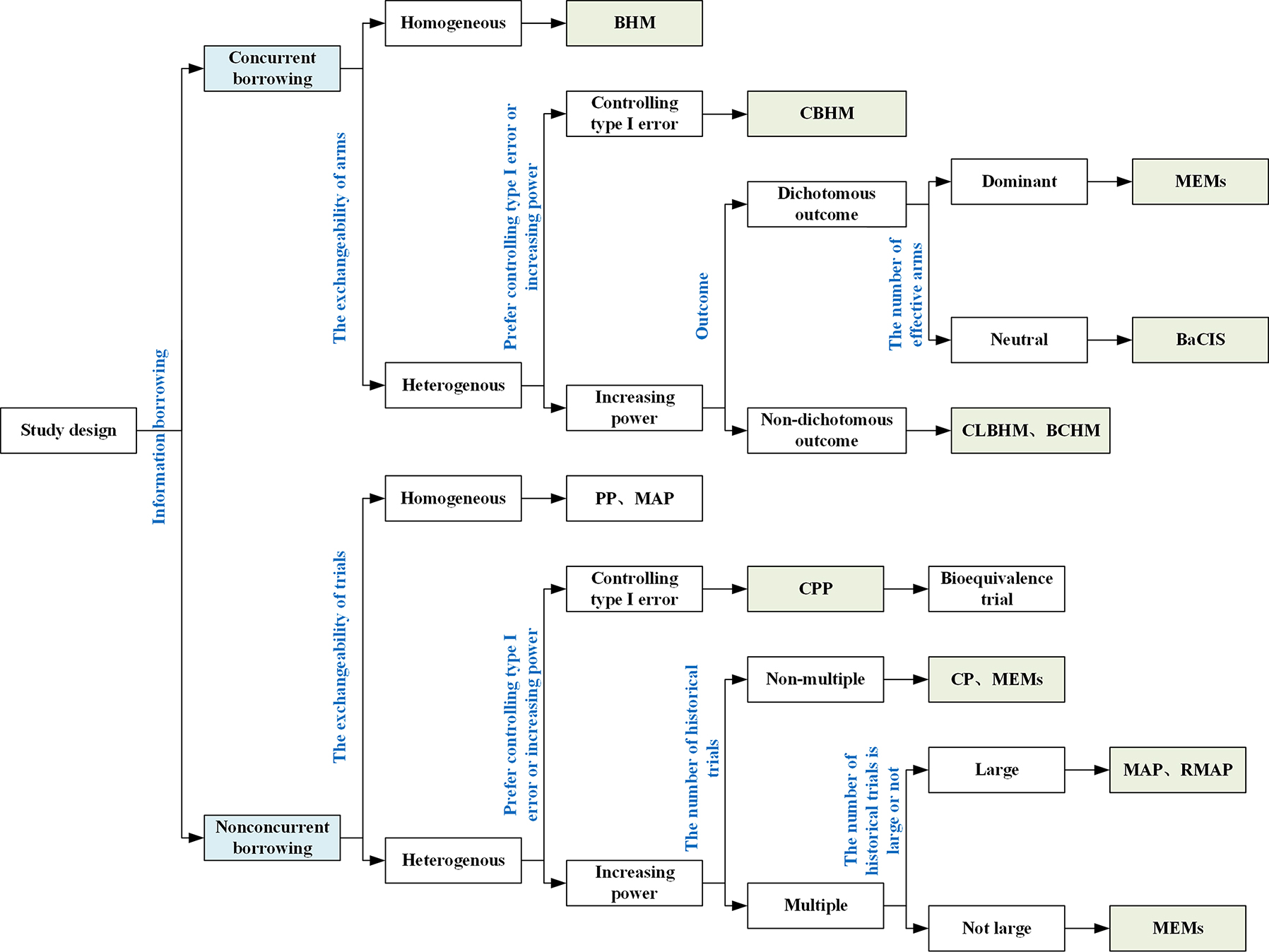
Application scenarios of the Bayesian information borrowing methods. BHM, Bayesian hierarchical model; CBHM, calibrated Bayesian hierarchical model; CLBHM, clustered Bayesian hierarchical model; BaCIS, Bayesian hierarchical classification and information sharing; BCHM, Bayesian cluster hierarchical model; MEMs, multisource exchangeability models; PP, power prior; MPP, modified power prior; CPP, calibrated power prior; CP, commensurate power prior; MAP, meta-analytic-predictive prior; RMAP, robust meta-analytic-predictive prior.
Concurrent borrowing methods are useful for applications involving multiple parallel arms, such as basket and platform trials. To choose an appropriate concurrent borrowing method, we should consider exchangeability, statistical performance, types of outcomes, and the number of effective arms. When all arms are homogeneous, the BHM approach is recommended because it shows greater power than other methods. In practice, it is more common that arms are heterogenous or could not be determine the exchangeability. CBHM with a function of heterogeneity measurement, and CLBHM, BaCIS and BCHM with dynamic clustering are recommended. CBHM shows better performance in controlling type I error, whereas CLBHM, BaCIS and BCHM often yield higher power. In addition, when the outcome is ordinal, BCHM tends to gain greater power. MEMs are recommended when the majority of arms are expected to be effective. In terms of balancing type I error and power gain, CLBHM often outperforms BaCIS, BCHM and MEMs, and also is much easier to implement.
Nonconcurrent borrowing methods are appropriate for applications intended to borrow information from external data or supplementary trials. Again, to choose an appropriate method, we should consider exchangeability, statistical performance, and the number of historical trials. When heterogeneity exists, PP and MAP lead to substantial type I error inflation. In this case, their extensions should be considered to obtain better type I error control. For example, CPP provides a stricter criterion for controlling type I error which is recommended to apply in bioequivalence trial. CP and RMAP place more weight on power gains. SAM prior has the best overall performance in improving power and controlling type I error, due to its ability to adaptively adjust the mixture weight based on the prior-data conflict. In addition, when the number of historical trials is small, it is not appropriated to apply MAP and RMAP, and MEMs should be considered.
Moreover, when patient-level covariates are different among different data sources, the PS-integrated priors approach are recommended. PS-MAP and PS-RMAP are recommended to deal with multiple external data sources because of the ability of type I error controlling [16, 17]. In particular, PS-RMAP considers heterogeneity not only between the current study and the external data sources but also between the external data sources themselves. However, the simulation study of Lu et al. showed that their extended PS-PP approach could have better performance than others in type I error controlling when multiple external data sources exist [102]. Therefore, the more comprehensive simulation studies are needed to assess the application scenarios of these available PS-integrated approaches.
Finally, to choose and use any borrowing information method, we should conduct comprehensive simulation study to evaluate its operating characteristics, e.g., the type I and type II error rates [8]. It is critical to balance power gain and type I error control. Justifying the choice of the borrowing information also requires a great deal of communication between the medical device sponsors and the regulatory agency.
Bayesian statistical software
Bayesian statistical software includes R, Stan, SAS, WinBUGS, Python and et al. R is more available and updates more timely than other software. Moreover, R has the interface to Stan and WinBUGS that provides more comprehensive and friendly operation to researchers. Therefore, R has become the most commonly used software in practice. Table 3 summarizes the available R packages and their functions. Stan is for Bayesian modeling and inference that primarily uses the No-U-Turn sampler (NUTS) to obtain posterior simulations. The R package RStan provides the function of Stan allowing one to conveniently fit Stan models from R and access the output, including posterior inferences and intermediate quantities such as evaluations of the log posterior density and its gradients [107]. The R package SAMprior can be used to dynamically borrow information from single to multiple external RWDs based on the SAM prior method [96]. The R package psrwe [112] and RBesT [113] focus on the PS-integrated methods for incorporating external RWD in clinical studies and synthesize the evidence.
Description of the available R packages and their functions.
| R packages | Functions | Access |
|---|---|---|
| RStan | Interface to software Stan | Stan development Team [107] |
| R2WinBUGS | Interface to BUGS | Gelman et al. [108] |
| mcmc | Simulating continuous distributions of random vectors using Markov chain Monte Carlo (MCMC) | Geyer et al. [109] |
| MCMCpack | Containing functions to perform Bayesian inference using posterior simulation for a number of statistical models | Martin et al. [110] |
| CODA | Output analysis and diagnostics for MCMC | Plummer et al. [111] |
| SAMprior | Dynamical borrowing information from single to multiple external RWDs based on the SAM prior method | Yang et al. [96] |
| psrwe | PS-integrated methods for incorporating external RWDs in clinical studies | Wang et al. [112] |
| RBesT | Bayesian evidence synthesis tools | Weber et al. [113] |
Discussion
Current situations
The FDA and Bayesian statisticians have been working collaboratively to develop Bayesian methodologies for medical device clinical studies since 1998. Nowadays, the Bayesian approach for design and analysis of medical device clinical studies has increased dramatically. This paper summarizes Bayesian designs which are commonly used in the medical device regulatory setting, and reviews several Bayesian information borrowing methods in the era of modern clinical studies and discusses their appropriate application scenarios.
The Bayesian approach provides greater flexibility in study designs compared to the frequentist approach. Bayesian adaptive study design could adjust design elements (e.g., go/no-go, sample size, and population) based on the accumulating data. There have been 9 medical devices with the Bayesian adaptive design acquiring the FDA approval according to the PMA Database since 1998, mainly in cardiovascular and orthopedic regions [25], [26], [27, 57], [58], [59, 61, 68, 74]. They tended to have slow accrual rate but need long follow-up, which is particularly suitable to use the Bayesian adaptive design to reduce sample size and shorten the length of studies. Moreover, the Bayesian approach also has great potential in multiregional studies. The regional variability could be captured by the Bayesian hierarchical model, while allowing information borrowing across regions. This might be difficult to achieve by the frequentist approach. In addition, with the rapid accumulation of RWD in the era of modern clinical studies, the Bayesian approach has been used for label expansion benefiting from its borrowing safety information from registered indication [20, 38]. The above applications in the Bayesian approach have unprecedentedly facilitated medical device registrations.
With the establishment of large cohorts and databases in the era of modern clinical studies, abundant data sources provide opportunities to borrow information to improve trial efficiency. In this paper, we discuss several commonly used information borrowing methods in both concurrent and nonconcurrent borrowing and their appropriate application scenarios. The specification of the borrowing strength parameter is challenging for many information borrowing methods. Numerous researchers are developing innovative methods to achieve more dynamic or adaptive information borrowing to offer better bias and type I error control. From the point of view of regulator, empirically specifying and data driven are the two common ways to determine the borrowing strength parameter. In the empirically specifying approach, communication with clinical investigators and regulator or reference to published studies could obtain the recommended values. In the data driven approach, estimation according to the heterogeneity [85] or model averaging/selection to fit the value [114] may be considered. As for the choice of information borrowing methods, though we discuss their recommended application scenarios, sufficient simulations are also needed to examine the statistical performance to provide the methodology basis for the discussion with regulator.
There are several limitations in the Bayesian approach. The pure Bayesian statistics do not include frequentist operating characteristics, such as type I error and power. Therefore, it is challenging to justify a Bayesian study in the regulatory setting. In practice, the Bayesian approach is used as an expansion tool for the frequentist approach in most cases. Hybrid Bayesian is based on the principles of Bayesian statistics, and combined with the evaluation of frequentist statistical operating characteristics. It could realize flexible design and analysis, and ensure more patients receiving effective treatments from an ethical perspective without sacrificing the integrity of clinical studies and the necessary statistical operating characteristics.
Future and challenges
With the rapid development of medical devices, there has been an increase in the use of Bayesian designs and analysis for regulatory purposes.
The Bayesian approach integrated with propensity score (PS) will play an important role in real-world evidence (RWE) synthesis. It is very common that patient covariates are different in different studies or databases. PS-integrated prior could not only exert the advantages of information borrowing from Bayesian models but also minimize bias from multisource external data. Researchers are developing various methods that integrated PS appropriately into informative prior based on the available methods [14]. With the development of real-world study (RWD) in the era of modern clinical studies, the role of the Bayesian approach integrated with PS on the bias controlling will receive more and more attention.
The Bayesian approach has the potential use in the mock trial design under the virtual patient framework. In 2015, the Medical Device Innovation Consortium (MDIC) virtual patient working group cooperated with FDA stating the method of assessing fatigue fracture in a hypothetical new ICD lead by a mock trial design. Virtual patients were generated from in-silico models of lead failures [115], and prior information was provided by phantoms [116].
Another potential use of the Bayesian approach is incorporating with artificial intelligence (AI)/machine learning (ML) in diagnostic device clinical studies. Compared to almost non-Bayesian ML models, Bayesian ML models could automatically provide uncertainty quantification of model output through the posterior distribution [117]. However, the current computational algorithms for fitting fully Bayesian ML models have not been satisfactory [118]. This will be the next research direction of the relative region.
The National Institutes of Health (NIH) issued the Adaptive Designs Accelerating Promising Trials into Treatments (ADAPT-IT) funding to encourage the Bayesian medical device studies [119]. The National Science Foundation also considered nonparametric Bayesian methods as a great development and Bayesian computation with complex modeling as useful in a wide range of applications [120]. Moreover, the Bayesian approach in evidence-based medicine (EBM) are mentioned and emphasized in medical student teaching [121].
The future for the Bayesian approach in total medicine and medical devices is bright. Using the Bayesian approach has great potential to accelerate the development of innovative medical devices and their accessibility to patients for disease diagnoses and treatments.
Funding source: The Real World Study Project of Hainan Baoao Lecheng Pilot Zone (Real World Study Base of National Medical Products Administration)
Award Identifier / Grant number: HNLC2022RWS017
Funding source: The National Key Research and Development Program of China
Award Identifier / Grant number: 2020YFC2006400
-
Ethical approval: Not applicable.
-
Informed consent: Not applicable.
-
Author contributions: Han Cao: Investigation, Methodology, Visualization, Writing - original draft. Chen Yao: Conceptualization, Investigation, Writing -review & editing, Supervision. Ying Yuan: Conceptualization, Writing -review & editing, Supervision.
-
Competing interests: Authors state no conflict of interest.
-
Research funding: This work was supported by The Real World Study Project of Hainan Boao Lecheng Pilot Zone (Real World Study Base of National Medical Products Administration, grant number HNLC2022RWS017), and The National Key Research and Development Program of China (grant number 2020YFC2006400).
-
Data availability: This is a review and does not involve data availability.
References
1. Berger, Z. Bayesian and frequentist models: legitimate choices for different purposes of clinical research. J Eval Clin Pract 2010;16:1045–7. https://doi.org/10.1111/j.1365-2753.2009.01247.x.Search in Google Scholar PubMed
2. Ventz, S, Trippa, L. Bayesian designs and the control of frequentist characteristics: a practical solution. Biometrics 2015;71:218–26. https://doi.org/10.1111/biom.12226.Search in Google Scholar PubMed
3. Kruschke, JK, Liddell, TM. The Bayesian New Statistics: hypothesis testing, estimation, meta-analysis, and power analysis from a Bayesian perspective. Psychon Bull Rev 2018;25:178–206. https://doi.org/10.3758/s13423-016-1221-4.Search in Google Scholar PubMed
4. FDA. Master Protocols: Efficient clinical trial design strategies to expedite development of oncology drugs and biologics; 2018. https://www.fda.gov/media/120721/download2018 [Accessed 28 May 2023].Search in Google Scholar
5. FDA. Interacting with the FDA on complex innovative trial designs for drugs and biological products; 2020. https://www.fda.gov/media/130897/download2020 [Accessed 28 May 2023].Search in Google Scholar
6. FDA. A Bayesian approach to detection of treatment-related effects in toxicology studies by borrowing information from historical control animals; 2021. https://www.fda.gov/science-research/fda-science-forum/bayesian-approach-detection-treatment-related-effects-toxicology-studies-borrowing-information2021 [Accessed 28 May 2023].Search in Google Scholar
7. Bonangelino, P, Irony, T, Liang, S, Li, X, Mukhi, V, Ruan, S, et al.. Bayesian approaches in medical device clinical trials: a discussion with examples in the regulatory setting. J Biopharm Stat 2011;21:938–53. https://doi.org/10.1080/10543406.2011.589650.Search in Google Scholar PubMed
8. Tidwell, RSS, Peng, SA, Chen, M, Liu, DD, Yuan, Y, Lee, JJ. Bayesian clinical trials at the University of Texas MD Anderson cancer center: an update. Clin Trials 2019;16:645–56. https://doi.org/10.1177/1740774519871471.Search in Google Scholar PubMed PubMed Central
9. FDA. Guidance for the use of bayesian statistics in medical device clinical trials; 2010. https://www.fda.gov/media/71512/download2010 [Accessed 28 May 2023].Search in Google Scholar
10. Magalhães, T, Dinis-Oliveira, RJ, Taveira-Gomes, T. Digital health and big data analytics: implications of real-world evidence for clinicians and policymakers. Int J Environ Res Publ Health 2022;19. https://doi.org/10.3390/ijerph19148364.Search in Google Scholar PubMed PubMed Central
11. Su, L, Chen, X, Zhang, J, Yan, F. Comparative study of bayesian information borrowing methods in oncology clinical trials. JCO Precis Oncol 2022;6:e2100394. https://doi.org/10.1200/po.21.00394.Search in Google Scholar
12. FDA. The summaries of safety and effectiveness (SSEDs) of the premarket approvals; 2023. https://www.accessdata.fda.gov/scripts/cdrh/cfdocs/cfPMA/pma.cfm2023 [Accessed 3 Jun 2023].Search in Google Scholar
13. FDA. Summary of safety and effectiveness data of PMA P180036; 2019. https://www.accessdata.fda.gov/cdrh_docs/pdf18/P180036B.pdf2019 [Accessed 3 Jun 2023].Search in Google Scholar
14. Lin, J, Lin, J. Incorporating propensity scores for evidence synthesis under Bayesian framework: review and recommendations for clinical studies. J Biopharm Stat 2022;32:53–74. https://doi.org/10.1080/10543406.2021.1882481.Search in Google Scholar PubMed
15. Saville, BR, Connor, JT, Ayers, GD, Alvarez, J. The utility of Bayesian predictive probabilities for interim monitoring of clinical trials. Clin Trials 2014;11:485–93. https://doi.org/10.1177/1740774514531352.Search in Google Scholar PubMed PubMed Central
16. Hobbs, BP, Carlin, BP. Practical Bayesian design and analysis for drug and device clinical trials. J Biopharm Stat 2008;18:54–80. https://doi.org/10.1080/10543400701668266.Search in Google Scholar PubMed
17. Giovagnoli, A. The bayesian design of adaptive clinical trials. Int J Environ Res Publ Health 2021:18. https://doi.org/10.3390/ijerph18020530.Search in Google Scholar PubMed PubMed Central
18. Zhou, H, Lee, JJ, Yuan, Y. BOP2: bayesian optimal design for phase II clinical trials with simple and complex endpoints. Stat Med 2017;36:3302–14. https://doi.org/10.1002/sim.7338.Search in Google Scholar PubMed
19. Zhao, Y, Li, D, Liu, R, Yuan, Y. Bayesian optimal phase II designs with dual-criterion decision making. Pharmaceut Stat 2023;22:605–18. https://doi.org/10.1002/pst.2296.Search in Google Scholar PubMed
20. FDA. Summary of safety and effectiveness data of PMA P070015; 2015. https://www.accessdata.fda.gov/cdrh_docs/pdf7/P070015S128B.pdf2015 [Accessed 3 Jun 2023].Search in Google Scholar
21. Kaizer, AM, Koopmeiners, JS, Hobbs, BP. Bayesian hierarchical modeling based on multisource exchangeability. Biostatistics 2018;19:169–84. https://doi.org/10.1093/biostatistics/kxx031.Search in Google Scholar PubMed PubMed Central
22. Irony, T, Simon, R. Application of Bayesian methods to medical device trials, Becker, KM, Whyte, JJ, editors. New York: Humana Press; 2006.Search in Google Scholar
23. Campbell, G. Similarities and differences of Bayesian designs and adaptive designs for medical devices: a regulatory view. Stat Biopharm Res 2013;5:356–68. https://doi.org/10.1080/19466315.2013.846873.Search in Google Scholar
24. Berry, SM, Carlin, BP, Lee, JJ, Muller, P. Bayesian adaptive methods for clinical trials. Boca Raton, FL: CRC Press; 2011.10.1201/EBK1439825488Search in Google Scholar
25. FDA. Summary of safety and effectiveness data of PMA P150009; 2018. https://www.accessdata.fda.gov/cdrh_docs/pdf15/P150009b.pdf2018 [Accessed 3 Jun 2023].Search in Google Scholar
26. FDA. Summary of safety and effectiveness data of PMA P140004; 2015. https://www.accessdata.fda.gov/cdrh_docs/pdf14/P140004b.pdf2015 [Accessed 3 Jun 2023].Search in Google Scholar
27. FDA. Summary of safety and effectiveness data of PMA P100046; 2011. https://www.accessdata.fda.gov/cdrh_docs/pdf10/P100046B.pdf2011 [Accessed 3 Jun 2023].Search in Google Scholar
28. Ryan, EG, Lamb, SE, Williamson, E, Gates, S. Bayesian adaptive designs for multi-arm trials: an orthopaedic case study. Trials 2020;21:83. https://doi.org/10.1186/s13063-019-4021-0.Search in Google Scholar PubMed PubMed Central
29. FDA. Summary of safety and effectiveness data of PMA P030031; 2009. https://www.accessdata.fda.gov/cdrh_docs/pdf3/P030031S011B.pdf2009 [Accessed 3 Jun 2023].Search in Google Scholar
30. Pennello, GA. Bayesian analysis of diagnostic test accuracy when disease state is unverified for some subjects. J Biopharm Stat 2011;21:954–70. https://doi.org/10.1080/10543406.2011.590921.Search in Google Scholar PubMed
31. ICH. Ethnic factors in the acceptability of foreign clinical data (R1); 1998. http://www.ich.org/fileadmin/Public_Web_Site/ICH_Products/Guidelines/Efficacy/E5_R1/Step4/E5_R1_Guideline.pdf1998 [Accessed 5 Jun 2023].Search in Google Scholar
32. Tsong, Y, Chang, WJ, Dong, X, Tsou, HH. Assessment of regional treatment effect in a multiregional clinical trial. J Biopharm Stat 2012;22:1019–36. https://doi.org/10.1080/10543406.2012.701583.Search in Google Scholar PubMed
33. Bean, NW, Ibrahim, JG, Psioda, MA. Bayesian design of multi-regional clinical trials with time-to-event endpoints. Biometrics 2023.10.1111/biom.13820Search in Google Scholar PubMed
34. Chen, YH, Wu, YC, Wang, M. A Bayesian approach to evaluating regional treatment effect in a multiregional trial. J Biopharm Stat 2009;19:900–15. https://doi.org/10.1080/10543400903105471.Search in Google Scholar PubMed
35. Bayman, EO. Bayesian hierarchical models for multi-center clinical trials: power and subgroup analyses. Ames.: University of Iowa; 2008.Search in Google Scholar
36. Deng, Y, Zhang, X, Long, Q. Bayesian modeling and prediction of accrual in multi-regional clinical trials. Stat Methods Med Res 2017;26:752–65. https://doi.org/10.1177/0962280214557581.Search in Google Scholar PubMed PubMed Central
37. FDA. Use of real world evidence to support regulatory decision making for medical devices; 2017. https://www.fda.gov/regulatory-information/search-fda-guidance-documents/use-real-world-evidence-support-regulatory-decision-making-medical-devices2017 [Accessed 28 May 2023].Search in Google Scholar
38. FDA. Summary of safety and effectiveness data of PMA P970003; 2017. https://www.accessdata.fda.gov/cdrh_docs/pdf/P970003s207b.pdf2017 [Accessed 3 Jun 2023].Search in Google Scholar
39. FDA. Summary of safety and effectiveness data of PMA 970033; 1999. https://www.accessdata.fda.gov/cdrh_docs/pdf/P970033B.pdf1999 [Accessed 3 Jun 2023].Search in Google Scholar
40. FDA. Summary of safety and effectiveness data of PMA P970015; 1999. https://www.accessdata.fda.gov/cdrh_docs/pdf/P970015b.pdf1999 [Accessed 3 Jun 2023].Search in Google Scholar
41. FDA. Summary of safety and effectiveness data of PMA 980048; 2001. https://www.accessdata.fda.gov/cdrh_docs/pdf/P980048b.pdf2001 [Accessed 3 Jun 2023].Search in Google Scholar
42. FDA. Summary of safety and effectiveness data of PMA P000053; 2001. https://www.accessdata.fda.gov/cdrh_docs/pdf/P000053b.pdf2001 [Accessed 3 Jun 2023].Search in Google Scholar
43. FDA. Summary of safety and effectiveness data of PMA P000036; 2001. https://www.accessdata.fda.gov/cdrh_docs/pdf/P000036b.pdf2001 [Accessed 3 Jun 2023].Search in Google Scholar
44. FDA. Summary of safety and effectiveness data of PMA P000028; 2002. https://www.accessdata.fda.gov/cdrh_docs/pdf/P000028b.pdf2002 [Accessed 3 Jun 2023].Search in Google Scholar
45. FDA. Summary of safety and effectiveness data of PMA P000058; 2002. https://www.accessdata.fda.gov/cdrh_docs/pdf/P000058b.pdf2002 [Accessed 3 Jun 2023].Search in Google Scholar
46. FDA. Summary of safety and effectiveness data of PMA P020014; 2002. http://www.fda.gov/ohrms/dockets/ac/02/slides/3905s1.htm2002 [Accessed 3 Jun 2023].Search in Google Scholar
47. FDA. Summary of safety and effectiveness data of PMA P020026; 2003. https://www.accessdata.fda.gov/cdrh_docs/pdf2/P020026b.pdf2003 [Accessed 3 Jun 2023].Search in Google Scholar
48. FDA. Summary of safety and effectiveness data of PMA P040021; 2005. https://www.accessdata.fda.gov/cdrh_docs/pdf4/P040021B.pdf2005 [Accessed 3 Jun 2023].Search in Google Scholar
49. FDA. Summary of safety and effectiveness data of PMA P060018; 2007. https://www.accessdata.fda.gov/cdrh_docs/pdf6/P060018b.pdf2007 [Accessed 3 Jun 2023].Search in Google Scholar
50. FDA. Summary of safety and effectiveness data of PMA P040021/S004; 2007. https://www.accessdata.fda.gov/cdrh_docs/pdf4/P040021s004b.pdf2007 [Accessed 3 Jun 2023].Search in Google Scholar
51. FDA. Summary of safety and effectiveness data of PMA P080007; 2008. https://www.accessdata.fda.gov/cdrh_docs/pdf8/P080007b.pdf2008 [Accessed 3 Jun 2023].Search in Google Scholar
52. FDA. Summary of safety and effectiveness data of PMA P060023; 2009. https://www.accessdata.fda.gov/cdrh_docs/pdf6/P060023B.pdf2009 [Accessed 3 Jun 2023].Search in Google Scholar
53. FDA. Summary of safety and effectiveness data of PMA 080032; 2010. https://www.accessdata.fda.gov/cdrh_docs/pdf8/P080032B.pdf2010 [Accessed 3 Jun 2023].Search in Google Scholar
54. FDA. Summary of safety and effectiveness data of PMA P100018; 2011. https://www.accessdata.fda.gov/cdrh_docs/pdf10/P100018B.pdf2011 [Accessed 3 Jun 2023].Search in Google Scholar
55. FDA. Summary of safety and effectiveness data of PMA P100003; 2012. https://www.accessdata.fda.gov/cdrh_docs/pdf10/P100003B.pdf2012 [Accessed 3 Jun 2023].Search in Google Scholar
56. FDA. Summary of safety and effectiveness data of PMA P110008; 2012. https://www.accessdata.fda.gov/cdrh_docs/pdf11/P110008B.pdf2012 [Accessed 3 Jun 2023].Search in Google Scholar
57. FDA. Summary of safety and effectiveness data of PMA P040043; 2013. https://www.accessdata.fda.gov/cdrh_docs/pdf4/P040043S051B.pdf2013 [Accessed 3 Jun 2023].Search in Google Scholar
58. FDA. Summary of safety and effectiveness data of PMA P010015; 2014. https://www.accessdata.fda.gov/cdrh_docs/pdf/P010015s205b.pdf2014 [Accessed 3 Jun 2023].Search in Google Scholar
59. FDA. Summary of safety and effectiveness data of PMA P010031; 2014. https://www.accessdata.fda.gov/cdrh_docs/pdf/P010015s205b.pdf2014 [Accessed 3 Jun 2023].Search in Google Scholar
60. FDA. Summary of safety and effectiveness data of PMA P090029; 2014. https://www.accessdata.fda.gov/cdrh_docs/pdf9/P090029b.pdf2014 [Accessed 3 Jun 2023].Search in Google Scholar
61. FDA. Summary of safety and effectiveness data of PMA P130013; 2015. https://www.accessdata.fda.gov/cdrh_docs/pdf13/P130013b.pdf2015 [Accessed 3 Jun 2023].Search in Google Scholar
62. FDA. Summary of safety and effectiveness data of PMA P150010; 2015. https://www.accessdata.fda.gov/cdrh_docs/pdf15/P150010B.pdf2015 [Accessed 3 Jun 2023].Search in Google Scholar
63. FDA. Summary of safety and effectiveness data of PMA P140005; 2015. https://www.accessdata.fda.gov/cdrh_docs/pdf14/P140005B.pdf2015 [Accessed 3 Jun 2023].Search in Google Scholar
64. FDA. Summary of safety and effectiveness data of PMA P110019; 2015. https://www.accessdata.fda.gov/cdrh_docs/pdf11/P110019s075b.pdf2015 [Accessed 3 Jun 2023].Search in Google Scholar
65. FDA. Summary of safety and effectiveness data of PMA P160050; 2016. https://www.accessdata.fda.gov/cdrh_docs/pdf16/P160050b.pdf2016 [Accessed 3 Jun 2023].Search in Google Scholar
66. FDA. Summary of safety and effectiveness data of PMA P090029; 2016. https://www.accessdata.fda.gov/cdrh_docs/pdf9/P090029s003b.pdf2016 [Accessed 3 Jun 2023].Search in Google Scholar
67. FDA. Summary of safety and effectiveness data of PMA P170019; 2016. https://www.accessdata.fda.gov/cdrh_docs/pdf17/P170019B.pdf2016 [Accessed 3 Jun 2023].Search in Google Scholar
68. FDA. Summary of safety and effectiveness data of PMA P130021; 2017. https://www.accessdata.fda.gov/cdrh_docs/pdf13/P130021S033b.pdf2017 [Accessed 3 Jun 2023].Search in Google Scholar
69. FDA. Summary of safety and effectiveness data of PMA P160018; 2017. https://www.accessdata.fda.gov/cdrh_docs/pdf16/P160018B.pdf2017 [Accessed 3 Jun 2023].Search in Google Scholar
70. FDA. Summary of safety and effectiveness data of PMA P170013; 2018. https://www.accessdata.fda.gov/cdrh_docs/pdf17/P170013b.pdf2018 [Accessed 3 Jun 2023].Search in Google Scholar
71. FDA. Summary of safety and effectiveness data of PMA P180007; 2018. https://www.accessdata.fda.gov/cdrh_docs/pdf18/P180007b.pdf2018 [Accessed 3 Jun 2023].Search in Google Scholar
72. FDA. Summary of safety and effectiveness data of PMA P170030; 2019. https://www.accessdata.fda.gov/cdrh_docs/pdf17/P170030b.pdf2019 [Accessed 3 Jun 2023].Search in Google Scholar
73. FDA. Summary of safety and effectiveness data of PMA P170027; 2019. https://www.accessdata.fda.gov/cdrh_docs/pdf17/P170027b.pdf2019 [Accessed 3 Jun 2023].Search in Google Scholar
74. FDA. Summary of safety and effectiveness data of PMA P180050; 2019. https://www.accessdata.fda.gov/cdrh_docs/pdf18/P180050b.pdf2019 [Accessed 3 Jun 2023].Search in Google Scholar
75. FDA. Summary of safety and effectiveness data of PMA P190016; 2019. https://www.accessdata.fda.gov/cdrh_docs/pdf19/P190016B.pdf2019 [Accessed 3 Jun 2023].Search in Google Scholar
76. FDA. Summary of safety and effectiveness data of PMA P180027; 2019. https://www.accessdata.fda.gov/cdrh_docs/pdf18/P180027B.pdf2019 [Accessed 3 Jun 2023].Search in Google Scholar
77. FDA. Summary of safety and effectiveness data of PMA P190019; 2020. https://www.accessdata.fda.gov/cdrh_docs/pdf19/P190019B.pdf2020 [Accessed 3 Jun 2023].Search in Google Scholar
78. FDA. Summary of safety and effectiveness data of PMA P210034; 2022. https://www.accessdata.fda.gov/cdrh_docs/pdf21/P210034B.pdf2022 [Accessed 3 Jun 2023].Search in Google Scholar
79. Nanda, R, Liu, MC, Yau, C, Shatsky, R, Pusztai, L, Wallace, A, et al.. Effect of pembrolizumab plus neoadjuvant chemotherapy on pathologic complete response in women with early-stage breast cancer: an analysis of the ongoing phase 2 adaptively randomized I-SPY2 trial. JAMA Oncol 2020;6:676–84. https://doi.org/10.1001/jamaoncol.2019.6650.Search in Google Scholar PubMed PubMed Central
80. Thall, PF, Wathen, JK, Bekele, BN, Champlin, RE, Baker, LH, Benjamin, RS. Hierarchical Bayesian approaches to phase II trials in diseases with multiple subtypes. Stat Med 2003;22:763–80. https://doi.org/10.1002/sim.1399.Search in Google Scholar PubMed
81. Chu, Y, Yuan, Y. A Bayesian basket trial design using a calibrated Bayesian hierarchical model. Clin Trials 2018;15:149–58. https://doi.org/10.1177/1740774518755122.Search in Google Scholar PubMed PubMed Central
82. Chen, N, Lee, JJ. Bayesian hierarchical classification and information sharing for clinical trials with subgroups and binary outcomes. Biom J 2019;61:1219–31. https://doi.org/10.1002/bimj.201700275.Search in Google Scholar PubMed PubMed Central
83. Chen, N, Lee, JJ. Bayesian cluster hierarchical model for subgroup borrowing in the design and analysis of basket trials with binary endpoints. Stat Methods Med Res 2020;29:2717–32. https://doi.org/10.1177/0962280220910186.Search in Google Scholar PubMed
84. Jiang, L, Li, R, Yan, F, Yap, TA, Yuan, Y. Shotgun: a Bayesian seamless phase I–II design to accelerate the development of targeted therapies and immunotherapy. Contemp Clin Trials 2021;104:106338. https://doi.org/10.1016/j.cct.2021.106338.Search in Google Scholar PubMed PubMed Central
85. Hobbs, BP, Landin, R. Bayesian basket trial design with exchangeability monitoring. Stat Med 2018;37:3557–72. https://doi.org/10.1002/sim.7893.Search in Google Scholar PubMed
86. Chen, IMH, Ibrahim, JG. Power prior distributions for regression models. Stat Sci 2000;15:46–60. https://doi.org/10.1214/ss/1009212673.Search in Google Scholar
87. Han, Z, Zhang, Q, Wang, M, Ye, K, Chen, MH. On efficient posterior inference in normalized power prior Bayesian analysis. Biom J 2023;65:e2200194. https://doi.org/10.1002/bimj.202200194.Search in Google Scholar PubMed
88. FDA. Summary of safety and effectiveness data of PMA P160052; 2022. https://www.accessdata.fda.gov/cdrh_docs/pdf16/P160052B.pdf2022 [Accessed 3 Jun 2023].Search in Google Scholar
89. Duan, Y, Ye, K, Smith, EP. Evaluating water quality using power priors to incorporate historical information. Environmetrics 2006;17:95–106. https://doi.org/10.1002/env.752.Search in Google Scholar
90. Pan, H, Yuan, Y, Xia, J. A calibrated power prior approach to borrow information from historical data with application to biosimilar clinical trials. J R Stat Soc Ser C Appl Stat 2017;66:979–96. https://doi.org/10.1111/rssc.12204.Search in Google Scholar PubMed PubMed Central
91. Hobbs, BP, Carlin, BP, Mandrekar, SJ, Sargent, DJ. Hierarchical commensurate and power prior models for adaptive incorporation of historical information in clinical trials. Biometrics 2011;67:1047–56. https://doi.org/10.1111/j.1541-0420.2011.01564.x.Search in Google Scholar PubMed PubMed Central
92. Hobbs, BP, Carlin, BP, Sargent, DJ. Adaptive adjustment of the randomization ratio using historical control data. Clin Trials 2013;10:430–40. https://doi.org/10.1177/1740774513483934.Search in Google Scholar PubMed PubMed Central
93. Jiang, L, Nie, L, Yuan, Y. Elastic priors to dynamically borrow information from historical data in clinical trials. Biometrics 2023;79:49–60. https://doi.org/10.1111/biom.13551.Search in Google Scholar PubMed
94. Neuenschwander, B, Capkun-Niggli, G, Branson, M, Spiegelhalter, DJ. Summarizing historical information on controls in clinical trials. Clin Trials 2010;7:5–18. https://doi.org/10.1177/1740774509356002.Search in Google Scholar PubMed
95. Schmidli, H, Gsteiger, S, Roychoudhury, S, O’Hagan, A, Spiegelhalter, D, Neuenschwander, B. Robust meta-analytic-predictive priors in clinical trials with historical control information. Biometrics 2014;70:1023–32. https://doi.org/10.1111/biom.12242.Search in Google Scholar PubMed
96. Yang, P, Zhao, Y, Nie, L, Vallejo, J, Yuan, Y. SAM: self-adapting mixture prior to dynamically borrow information from historical data in clinical trials. Biometrics, to appear, arXiv (preprint); 2023:arXiv:2305.12279.10.1111/biom.13927Search in Google Scholar PubMed
97. Rosenbaum, PR, Rubin, DB. The central role of the propensity score in observational studies for causal effects. Biometrika 1983;70:41–55. https://doi.org/10.1093/biomet/70.1.41.Search in Google Scholar
98. Wang, C, Rosner, GL. A Bayesian nonparametric causal inference model for synthesizing randomized clinical trial and real-world evidence. Stat Med 2019;38:2573–88. https://doi.org/10.1002/sim.8134.Search in Google Scholar PubMed
99. Lin, J, Gamalo-Siebers, M, Tiwari, R. Propensity-score-based priors for Bayesian augmented control design. Pharmaceut Stat 2019;18:223–38. https://doi.org/10.1002/pst.1918.Search in Google Scholar PubMed
100. Yue, LQ, Campbell, G, Lu, N, Xu, Y, Zuckerman, B. Utilizing national and international registries to enhance pre-market medical device regulatory evaluation. J Biopharm Stat 2016;26:1136–45. https://doi.org/10.1080/10543406.2016.1226336.Search in Google Scholar PubMed
101. Yue, LQ. Regulatory considerations in the design of comparative observational studies using propensity scores. J Biopharm Stat 2012;22:1272–9. https://doi.org/10.1080/10543406.2012.715111.Search in Google Scholar PubMed
102. Wang, C, Li, H, Chen, WC, Lu, N, Tiwari, R, Xu, Y, et al.. Propensity score-integrated power prior approach for incorporating real-world evidence in single-arm clinical studies. J Biopharm Stat 2019;29:731–48. https://doi.org/10.1080/10543406.2019.1657133.Search in Google Scholar PubMed
103. Yue, LQ, Lu, N, Xu, Y. Designing premarket observational comparative studies using existing data as controls: challenges and opportunities. J Biopharm Stat 2014;24:994–1010. https://doi.org/10.1080/10543406.2014.926367.Search in Google Scholar PubMed
104. Lu, N, Wang, C, Chen, WC, Li, H, Song, C, Tiwari, R, et al.. Propensity score-integrated power prior approach for augmenting the control arm of a randomized controlled trial by incorporating multiple external data sources. J Biopharm Stat 2022;32:158–69. https://doi.org/10.1080/10543406.2021.1998098.Search in Google Scholar PubMed
105. Liu, M, Bunn, V, Hupf, B, Lin, J, Lin, J. Propensity-score-based meta-analytic predictive prior for incorporating real-world and historical data. Stat Med 2021;40:4794–808. https://doi.org/10.1002/sim.9095.Search in Google Scholar PubMed
106. Zhu, AY, Roy, D, Zhu, Z, Sailer, MO. Propensity score stratified MAP prior and posterior inference for incorporating information across multiple potentially heterogeneous data sources. J Biopharm Stat 2023:1–15. https://doi.org/10.1080/10543406.2023.2181354.Search in Google Scholar PubMed
107. Stan-Development-Team. RStan: the R interface to Stan; 2023. https://mirrors.sjtug.sjtu.edu.cn/cran/web/packages/rstan/vignettes/rstan.html2023 [Accessed 5 Jun 2023].Search in Google Scholar
108. Gelman, A, Sturtz, S, Ligges, U, Gorjanc, G, Kerman, J. R2WinBUGS; 2015. https://cran.r-project.org/web/packages/R2WinBUGS/index.html2015 [Accessed 5 Jun 2023].Search in Google Scholar
109. Geyer, CJ, Johnson, LT. mcmc; 2020. https://cran.r-project.org/web/packages/mcmc/index.html2020 [Accessed 5 Jun 2023].Search in Google Scholar
110. Martin, AD, Quinn, KM, Park, JH. MCMCpack: Markov chain Monte Carlo in R. J Stat Software 2011;42:1–21. https://doi.org/10.18637/jss.v042.i09.Search in Google Scholar
111. Plummer, M. R-beta: CODA package for R; 2006. https://stat.ethz.ch/pipermail/r-help/1998-May/002474.html2006 [Accessed 5 Jun 2023].Search in Google Scholar
112. Wang, C. Psrwe: propensity score-integrated methods for incorporating real-world evidence in clinical studies; 2022. https://mirrors.sjtug.sjtu.edu.cn/cran/web/packages/psrwe/vignettes/vignette.html2022 [Accessed 5 Jun 2023].Search in Google Scholar
113. Weber, S, Li, Y, Seaman, JWIii, Kakizume, T, Schmidli, H, De Toni, E, et al.. Applying meta-analytic-predictive priors with the R bayesian evidence synthesis tools. J Stat Software 2021;100:1–32. https://doi.org/10.1159/000517158.Search in Google Scholar PubMed PubMed Central
114. Tang, R, Shen, J, Yuan, Y. ComPAS: A Bayesian drug combination platform trial design with adaptive shrinkage. Stat Med 2019;38:1120–34. https://doi.org/10.1002/sim.8026.Search in Google Scholar PubMed
115. Haddad, T, Himes, A, Thompson, L, Irony, T, Nair, R. Incorporation of stochastic engineering models as prior information in Bayesian medical device trials. J Biopharm Stat 2017;27:1089–103. https://doi.org/10.1080/10543406.2017.1300907.Search in Google Scholar PubMed
116. Badano, A, Graff, CG, Badal, A, Sharma, D, Zeng, R, Samuelson, FW, et al.. Evaluation of digital breast tomosynthesis as replacement of full-field digital mammography using an in silico imaging trial. JAMA Netw Open 2018;1:e185474. https://doi.org/10.1001/jamanetworkopen.2018.5474.Search in Google Scholar PubMed PubMed Central
117. Benjamens, S, Dhunnoo, P, Meskó, B. The state of artificial intelligence-based FDA-approved medical devices and algorithms: an online database. NPJ Digit Med 2020;3:118. https://doi.org/10.1038/s41746-020-00324-0.Search in Google Scholar PubMed PubMed Central
118. Dunson, DB. Statistics in the big data era: failures of the machine. Stat Probab Lett 2018;136. https://doi.org/10.1016/j.spl.2018.02.028.Search in Google Scholar
119. Meurer, WJ, Lewis, RJ, Tagle, D, Fetters, MD, Legocki, L, Berry, S, et al.. An overview of the adaptive designs accelerating promising trials into treatments (ADAPT-IT) project. Ann Emerg Med 2012;60:451–7. https://doi.org/10.1016/j.annemergmed.2012.01.020.Search in Google Scholar PubMed PubMed Central
120. He, X, Madigan, D, Yu, B, Wellner, J. Statistics at a crossroads: who is for the challenge; 2019. https://www.nsf.gov/mps/dms/documents/Statistics_at_a_Crossroads_Workshop_Report_2019.pdf2019 [Accessed 5 Jun 2023].Search in Google Scholar
121. Kurzenhäuser, S, Hoffrage, U. Teaching Bayesian reasoning: an evaluation of a classroom tutorial for medical students. Med Teach 2002;24:516–21. https://doi.org/10.1080/0142159021000012540.Search in Google Scholar PubMed
© 2023 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Articles in the same Issue
- Frontmatter
- Editorials
- The role of clinical trials in advancing reproductive medicine: a comprehensive overview
- New insights into non-invasive screening of esophageal squamous cell carcinoma
- Reviews
- The application of artificial intelligence in the management of sepsis
- Macrophages and microglia in inflammation and neuroinflammation underlying different pain states
- Bayesian approach for design and analysis of medical device trials in the era of modern clinical studies
- Nanostructured boron agents for boron neutron capture therapy: a review of recent patents
- Perspective
- Iron oxide nanoparticles in magnetic drug targeting and ferroptosis-based cancer therapy
Articles in the same Issue
- Frontmatter
- Editorials
- The role of clinical trials in advancing reproductive medicine: a comprehensive overview
- New insights into non-invasive screening of esophageal squamous cell carcinoma
- Reviews
- The application of artificial intelligence in the management of sepsis
- Macrophages and microglia in inflammation and neuroinflammation underlying different pain states
- Bayesian approach for design and analysis of medical device trials in the era of modern clinical studies
- Nanostructured boron agents for boron neutron capture therapy: a review of recent patents
- Perspective
- Iron oxide nanoparticles in magnetic drug targeting and ferroptosis-based cancer therapy


