Home On topological properties of hierarchical hypercube network based on Ve and Ev degree
Article Open Access

On topological properties of hierarchical hypercube network based on Ve and Ev degree

  • Nida Zahra EMAIL logo and Muhammad Ibrahim EMAIL logo
Published/Copyright: June 18, 2021
Download Article (PDF)
Main Group Metal Chemistry
From the journal Main Group Metal Chemistry Volume 44 Issue 1

Abstract

Grid implementation is a principal unit in electrical and electronic engineering but it depends on the domain of these projects. For example, depending on the grid and the signal processing in that fields of electronic and electrical engineering, such as more abstract mathematics in signal conversion and e-transmission theory griding, etc. Provides transmission through grid nodes. Graph theory is very useful in research fields. As topological indices, there are more actual numbers associated with chemical composition complaints connected to the chemical grid with physical and chemical properties and reactions. In this paper, we expand the work to interconnected grid and examine the first Zagreb, the second Zagreb, Randic, sum-connectivity, harmonic, geometric, and atom bond connectivity exponents of hierarchical hypercube network based on vertex-edge and edge-vertex degree.

Keywords: hierarchical hypercube network (HHN); edge-vertex degree; vertex-edge degree; molecular topological indices

1 Introduction

It usually requires a multi-processor interconnect grid to connect to thousands of analogs, copies of processor-memory pairs, each this pairing is called processing node. No need to use shared memory, all integration and transmission with processing nodes to execution of the program is usually completed by message transferring. Utilization and structure of various processor linkage grid is recently captured more attention due to accessibility of cheap, solid nano processor and bit cache. Web grid has been known as universal interconnection grid as a large-scale linkage parallel computing. Web/ring like low dimensional grid, they have received more consideration recently due to their improvement, compared to more complex grid, it can be extended to larger grid, such as hypercube. Especially failure has studied reliance on network collaboration (Gutman et al., 2012), which have a lot lately. Algorithm development on optical system and extremal weights of graph are studied by Al-Ayyoub et al. (2006) and Bollobas and Erdos (1998). Basic operations (Wang and Sahni, 1998a), image processing (Wang and Sahni, 2000), and many more about the OTIS-Mesh optoelectronic computer are studied by Wang and Sahni (1998b). To lessen the grid and to use the locus of transmission to lessen link costs exist in similar utilization, Hierarchical interconnection network (HIN) provide design framework. Various level are engaged by HIN. The core grid facilitates native transmission, whereas developed grids provides distant transmission. Various leveled grid have been in use for a long time. The transmission grid performs similar calculations (Konstantinidou, 1992). Some web networking topology characteristics are studied in Aslam et al. (2017), Baig and Naeem (2018), Hayat and Imran (2014), and Shao et al. (2018). Chemicals composite and their structure are designed by molecular diagrams. A molecular design is a design of atoms as points of the given structure and links are their linkage. Topological indices is a digital figure related to the structure describe the topological feature. It is invariant under the automorphism of the graph. More briefly, the topological descriptor, the Top(G) of graph G is a number, and each graph H that is isomorphic to graph G, Top(H) = Top(G). The work completed by Wiener (1947) gave the idea of topological descriptor, while working at the breaking point of the paraffin. He called this indices the routing number. Then, the routing number was recalled as Wiener indices. This topological descriptor had provided base to the topological indices, from the perspective of theory and application, for details, see Dobrynin et al. (2001), Estrada et al. (1998), and Gutman and Polansky (1986). So chemically and quantitatively literature, the most commonly used topological lesion are Wiener, Zagreb, Randic, and atom-bond connectivity (Chen et al. 2012; Das et al. 2011; Ediz 2017a, 2017b; Li et al., 2010; Wiener, 1947; Zhou and Trinajstiae 2010; Zhou et al., 2013). In any in this case, all the above work has been completed using the previous degree concepts. Later on, Chellali et al. (2017) discovered two new degree ideas in grid history, specifically, vertex-edge degree, and edge-vertex degree. Many researchers explore different networks by using these two new ideas such as Ediz (2018). These ideas are the transformation of previous degree-based concept (Estrada et al. 1998; Sahin and Ediz, 2018).

2 Preliminaries

This part comprises of some primary concepts related to graph which is usually represented by H = (V,E) where V represents collection of nodes and E is collection of links of graph. The total number of links attached to a node is degree of that node. In connected graph there exist adjacency of nodes. The open neighborhood, denoted by N(y), for a node y can be defined as the N(y) =x∈V| x y, ∈E. Similarly, the closed neighborhood of y, denoted by N[y], can be defined as If we add the node y to the collection of N(y), then we get the edge-vertex degree of the link f =xy∈E, denoted by ϕ˜ev(f) defined in Cancan (2019) is equal to the number of nodes in the union of the closed neighborhoods of x and y. Furthermore, The vertex-edge degree, denoted by ϕ˜ve(y) , defined in Cancan (2019) of the node y ∈V, is equal to the number of links that are joined to any nodes from the closed neighborhood of y but in this collection there is not repetition occur.

Let H be a simple graph and f =xy ∈ E(H). For detail associated to vertex-edge and edge-vertex degree topological indices, we mention (Cancan, 2019; Chellali et al., 2017).

In the given all descriptions, consider H be a simple graph and y ∈ V(H).

The edge-vertex degree Zagreb indices is defined as:

(1) ℳev(H)=∑f∈E(H)ϕ˜ev(f)2

The first vertex-edge degree Zagreb alpha indices is define as:

(2) ℳ1αve(H)=∑x∈V(G)ϕ˜ve(x)2

The first vertex-edge degree Zagreb beta indices is define as:

(3) ℳ1βve(H)=∑xy∈E(H)(ϕ˜ve(x)+ϕ˜ve(y))

The second vertex-edge degree Zagreb indices is define as:

(4) ℳ2ve(H)=∑xy∈E(H)(ϕ˜ve(x)×ϕ˜ve(y))

The vertex-edge degree Randic indices is define as:

(5) ℛve(H)=∑xy∈E(H)(ϕ˜ve(x)×ϕ˜ve(y))−12

The edge-vertex degree Randic indices is define as:

(6) ℛev(H)=∑f∈E(H)ϕ˜ve(f)−12

The vertex-edge degree atom-bond connectivity indices is define as:

(7) 𝒜ℬ𝒞ve(H)=∑xy∈E(H)ϕ˜ve(x)+ϕ˜ve(y)−2ϕ˜ve(x)+ϕ˜ve(y)

The vertex-edge degree geometric-arithmetic (ve-GA) indices is define as:

(8) 𝒢𝒜ve(H)=∑xy∈E(H)2ϕ˜ve(x)+ϕ˜ve(y)ϕ˜ve(x)+ϕ˜ve(y)

The vertex-edge degree harmonic (ve-H) indices is defined as:

(9) ℋve(H)=∑xy∈E(H)2ϕ˜ve(x)+ϕ˜ve(y)

The vertex-edge degree sum-connectivity (ve-χ) indices is defined as:

(10) χve(H)=∑xy∈E(H)(ϕ˜ve(x)×ϕ˜ve(y))−12

3 Hierarchical hypercube network (HHN-1)n×n

In this segment, we determine some vertex-edge and edge-vertex degree based topological indices for hierarchical hypercube network (HHN−1), from Guirao et al. (2018), see Figure 1. Let (HHN−1)n×n be a hierarchical hypercube network. The (HHN−1)n×n have 16n + 16 nodes and 24n + 20 links. We divide the link collection with respect to the degrees of end nodes of each link of (HHN−1)n×n into two component. One link component E1((HHN−1)n×n) comprises of 16 links uv, where deg(u) = 2, deg(v) = 3. The other link part E2((HHN−1)n×n) comprises of 24n + 4 links uv, where deg(u) = deg(v) = 3.

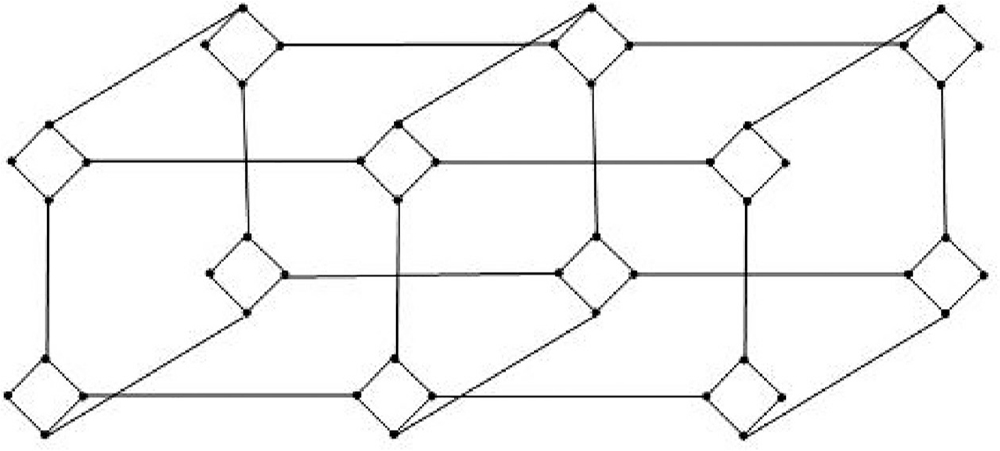
Figure 1 Hierarchical hypercube network (HNN-1)2×2.
Figure 1

Hierarchical hypercube network (HNN-1)2×2.

Similarly, we divide the node collection with respect to the degrees of nodes into two components. One component comprises the 8 nodes with degree 2 and the other is comprises the 16n + 8 nodes with degree 3.

We splits the links, based on edge-vertex degree of the (HHN−1)n×n for n ≥ 2 in Table 1. Similarly, we splits the nodes and links, based on vertex-edge degree of (HHN−1)n×n for n ≥ 2 in Tables 2 and 3.

Table 1

Link partitioning of (HHN − 1)n×n

No. of links Deg of end nodes Edge-vertex degrees
16 (2,3) 5
24n + 4 (3,3) 6
Table 2

Nodes partitioning of (HHN − 1)n×n

No. of nodes Deg(u) Vertex-edge degrees
8 2 6
16 3 8
16n − 8 3 9
Table 3

The vertex-edge degree of the end nodes of links of (HHN − 1)n×n

No. of links Deg of end nodes Vertex-edge degrees of end nodes
16 (2,3) (6,8)
16 (3,3) (8,9)
24n − 12 (3,3) (9,9)

3.1 Edge-vertex degree base indices

Now for the hierarchical hypercube network (HHN−1)n×n, we will determine Zagreb and Randic indices based on the edge-vertex degree.

3.1.1 Zagreb index

The Zagreb index using Table 1 is computed as:

ℳev(HHN−1)=∑f∈E(HHN−1)ϕ˜ev(f)2,ℳev(HHN−1)=16×52+(24n+4)×62=400+864n+144=864n+544.

3.1.2 The Randic index

The Randic index using Table 1 is computed as:

ℛev(HHN−1)=∑f∈E(HHN−1)ϕ˜ev(f)12,ℛev(HHN−1)=16×5−12+(24n+4)×6−12=165+246n+46=9.79n+8.78.

3.2 Vertex-edge degree base indices

Now for the hierarchical hypercube network (HHN−1)n×n, we will determine the vertex-edge degree based first Zagreb alpha, first Zagreb beta, the second Zagreb, Randic, atom-bond connectivity, geometric-arithmetic, harmonic, and sum-connectivity indices.

3.2.1 The first Zagreb alpha index

The first Zagreb alpha index using Table 2 can be computed as:

ℳ1αve(HHN−1)=∑x∈V(HHN−1)ϕ˜ve(x)2,ℳ1αve(HHN−1)=8×62+16×82+(16n−8)×92=288+1024+1296n−648=12964n+664.

3.2.2 The first Zagreb beta index

The first Zagreb beta index using Table 3 can be computed as:

ℳ1βve(HHN−1)=∑xy∈E(HHN−1)(ϕ˜ve(x)+ϕ˜ve(y)),ℳ1βve(HHN−1)=16×14+16×17+(24n−12)×18=224+272+432n−216=432n+280.

3.2.3 The second Zagreb index

The second Zagreb index using Table 3 can be computed as:

ℳ2ve(HHN−1)=∑xy∈E(HHN−1)(ϕ˜ve(x)+ϕ˜ve(y)),ℳ2ve(HHN−1)=16×48+16×72+(24n−12)×81=768+1152+1944n−972=1944n+948.

3.2.4 The Randic index

The Randic index using Table 3 can be computed as:

ℛve(HHN−1)=∑xy∈E(HHN−1)(ϕ˜ve(x)×ϕ˜ve(y))−12,ℛev(HHN−1)=16×48−12+16×72−12(24n−12)×81−12=43+832+83n−43=2.67n+2.86.

3.2.5 The atom-bond connectivity index

The atom-bond connectivity index using Table 3 can be computed as:

𝒜ℬ𝒞ve(HHN−1)=∑xy∈E(HHN−1)ϕ˜ve(x)+ϕ˜ve(y)−2ϕ˜ve(x)+ϕ˜ve(y),𝒜ℬ𝒞ve(HHN−1)=16×14−248+16×17−272+(24n−12)×18−281=8+8152+323n−163=10.67n+24.57.

3.2.6 The geometric-arithmetic index

The geometric arithmetic index using Table 3 can be computed as:

𝒢𝒜ve(HHN−1)=∑xy∈E(HHN−1)2ϕ˜ve(x)+ϕ˜ve(y)ϕ˜ve(x)+ϕ˜ve(y),𝒢𝒜ve(HHN−1)=16×24814+16×27217+(24n−12)×28118+6437+192217+24n−12=24n+19.81.

3.2.7 The harmonic index

The harmonic index using Table 3 can be computed as:

ℋve(HHN−1)=∑xy∈E(HHN−1)2ϕ˜ve(x)+ϕ˜ve(y),ℋve(HHN−1)=16×214+16×217+(24n−12)×218+167+3217+83n−43=2.67n+2.83.

3.2.8 The sum-connectivity index

The sum-connectivity index using Table 3 can be computed as:

χve(HHN−1)=∑xy∈E(HHN−1)(ϕ˜ve(x)+ϕ˜ve(y))−12,χve(HHN−1)=16×14−12+16×17−12+(24n−12)×18−12=1614+1617+82n−42=5.66n+5.33.

4 Hierarchical hypercube network (HHN−2)n×n

In this segment, we determine some vertex-edge and edge-vertex degree based topological indices for hierarchical hypercube network (HHN−2), from Guirao et al. (2018), see in Figure 2. The (HHN−2)n×n have 16n + 16 nodes and 32n + 28 links. We divide the link collection with respect to the degrees of end nodes of each link of (HHN−2)n×n into two components. One link component E1((HHN−2)n×n) comprises of 24 links uv, where deg(u) = 3, deg(v) = 4. The other link component E2((HHN−2)n×n) comprises of 32n + 4 links uv, where deg(u) = deg(v) = 4.

Figure 2 Hierarchical hypercube network (HNN-2)2×2.
Figure 2

Hierarchical hypercube network (HNN-2)2×2.

Similarly, we divide the node collection with respect to the degrees of nodes into two components. One component comprises of 8 nodes with degree 3 and the other component comprises of 16n + 8 nodes with degree 4.

We split the links, based on edge-vertex degree of the (HHN−2)n×n for n ≥ 2 in Table 4. Similarly, we divide the nodes and links, based on vertex-edge degree of (HHN−2)n×n for n ≥ 2 in Tables 5 and 6.

Table 4

Link partitioning of (HHN − 2)n×n

No. of links Deg of end nodes Edge-vertex degrees
24 (3,4) 5
24n (4,4) 6
8n + 4 (4,4) 8
Table 5

Nodes partitioning of (HHN − 2)n×n

No. of nodes Deg(u) Vertex-edge degrees
8 3 9
24 4 12
16n − 16 4 13
Table 6

The vertex-edge degree of the end nodes of links of (HHN − 2)n×n.

No. of links Deg of end nodes Vertex-edge degrees of end nodes
24 (3,4) (9,12)
32 (4,4) (12,12)
8 (4,4) (12,13)
32n − 36 (4,4) (13,13)

4.1 Edge-vertex degree base indices

Now for the hierarchical hypercube network (HHN−1)n×n we will compute Zagreb and Randic indices based on the edge-vertex degree.

4.1.1 Zagreb index

The Zagreb index using Table 4 can be computed as:

ℳev(HHN−2)=∑e∈E(HHN−1)(ϕ˜ev(e)2),ℳev(HHN−2)=24×52+24n×62+(8n+4)×82=600+864n+512n+256=1376n+856.

4.1.2 The Randic index

The Randic index using Table 4 can be computed as:

ℛev(HHN−2)=∑e∈E(HHN−1)ϕ˜ev(e)−12,ℛev(HHN−2)=24×5−12+24n×6−12+(8n+4)×8−12=245+246n+42n+22=12.63n+12.15.

4.2 Vertex-edge degree base indices

Now for the hierarchical hypercube network (HHN−1)n×n, we will compute first Zagreb alpha, first Zagreb beta, the second Zagreb, Randic, atom-bond connectivity, geometric-arithmetic, harmonic, and sum-connectivity indices based on the vertex-edge degree.

4.2.1 The first Zagreb alpha index

The first Zagreb alpha index using Table 5 can be computed as:

ℳ1αve(HHN−1)=∑v∈V(HHN−1)ϕ˜ve(v)2,ℳ1αve(HHN−1)=8×92+24×122+(16n−16)×132=648+3456+2704n−2704=2704n+1400.

4.2.2 The first Zagreb beta index

The first Zagreb beta index using Table 6 can be computed as:

ℳ1βve(HHN−2)=∑uv∈V(HHN−1)(ϕ˜ve(u)+ϕ˜ve(v)),ℳ1βve(HHN−2)=24×21+32×24+8×25+(32n−36)×26=504+768+200+832n−936=832n+536.

4.2.3 The second Zagreb index

The second Zagreb index using Table 6 can be computed as:

ℳ2ve(HHN−2)=∑uv∈E(HHN−1)(ϕ˜ve(u)×ϕ˜ve(v)),ℳ2ve(HHN−2)=24×108+32×144+8×156+(32n−36)×169=2592+4608+1248+5408n−6084=5408n+2364.

4.2.4 The Randic index

The Randic index using Table 6 can be computed as:

𝒣ve(HHN−2)=∑uv∈E(HHN−1)2ϕ˜ve(u)+ϕ˜ve(v),𝒣ve(HHN−2)=24×221+32×224+8225×(32n−36)×226+167+83+1625+3213n−3613=2.46n+2.82.

4.2.5 The atom-bond connectivity index

The atom-bond connectivity index using Table 6 can be computed as:

𝒜ℬ𝒞ve(HHN−2)=∑uv∈E(HHN−1)ϕ˜ve(u)+ϕ˜ve(v)−2ϕ˜ve(u)+ϕ˜ve(v),𝒜ℬ𝒞ve(HHN−2)=24×21−2108+32×24−2144+8×25−2156+(32n−36)×26−2169=4193+8223+42339+64613n−72613=12.06n+12.08.

4.2.6 The geometric-arithmetic index

The geometric arithmetic index using Table 6 can be computed as:

𝒢𝒜ve(HHN−2)=∑uv∈E(HHN−1)2ϕ˜ve(u)−ϕ˜ve(v)ϕ˜ve(u)−ϕ˜ve(v),𝒢𝒜ve(HHN−2)=24×210821+32×214424+8×215625+(32n−36)×216926=9637+32+323925+32n−36=32n+27.75.

4.2.7 The harmonic index

The harmonic index using Table 6 can be computed as:

𝒣ve(HHN−2)=∑uv∈E(HHN−1)2ϕ˜ve(u)+ϕ˜ve(v),𝒣ve(HHN−2)=24×221+32×224+8×225+(32n−36)×226+167+83+1625+3213n−3613=2.46n+2.82.

4.2.8 The sum-connectivity index

The sum-connectivity index using Table 6 can be computed as:

χve(HHN−2)=∑uv∈E(HHN−1)(ϕ˜ve(u)+ϕ˜ve(v))−12,χve(HHN−2)=24×21−12+32×24−12+8×25−12+(32n−36)×26−12=2421+166+85+3226n−3626=6.27n+6.31.

5 Graphical representation and discussion

In this part, we debate diagrammatically illustration relative to the edge-vertex degree and vertex-edge degree based topological indices for the hierarchical hypercube network (HHN − 1) and (HHN − 2). We manipulate the precise results for the edge-vertex degree based Zagreb and Randic indices, vertex-edge degree based First Zagreb alpha, first Zagreb beta, the second Zagreb, Randic, atom-bond connectivity (ve-𝒜ℬ𝒞), geometric-arithmetic (ve-𝒢𝒜), harmonic (ve-ℋ), and sum-connectivity (ve-χ) indices for the hierarchical hypercube network HHN −1 and HHN − 2.

The diagrammatically illustration of hierarchical hypercube network HHN −1 are given below. All indicators grow with growing values of n, can be noticed from given Figures 3 and 4. It can also be detected that vertex-edge degree based Randic and harmonic indices behave same for all values of n.

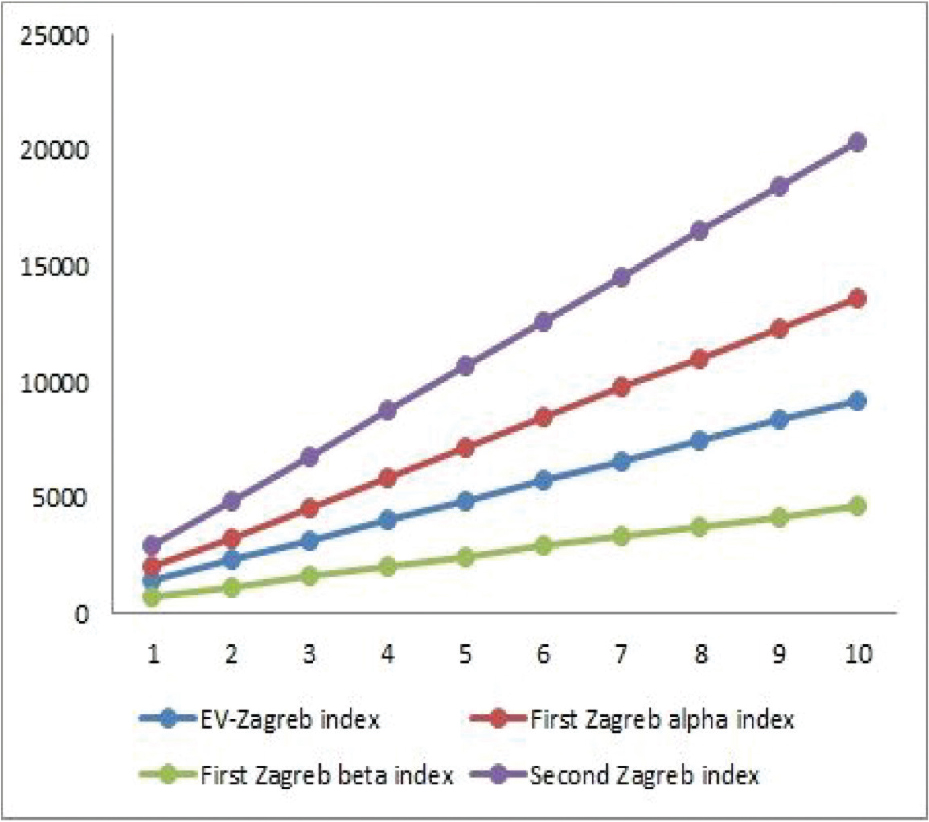
Figure 3 Graphical comparison of Mev, M1αve M_1^{\alpha ve} , M1βve M_1^{\beta ve} , and M2ve M_2^{ve} for HNN-1.
Figure 3

Graphical comparison of Mev, M1αve , M1βve , and M2ve for HNN-1.

Figure 4 Graphical comparison of Rev, GAve, ABCve Hve, Rve, and χve for HNN-1.
Figure 4

Graphical comparison of Rev, GAve, ABCve Hve, Rve, and χve for HNN-1.

Similarly, The diagrammatically illustration of hierarchical hypercube network HHN − 2 are given below. All indicators expand with expansion of n, can be noticed from given Figures 5 and 6. It can also be noticed that vertex-edge degree based Randic and harmonic indices act same for all values of n.

Figure 5 Graphical comparison of Mev, M1αve M_1^{\alpha ve} , M1βve M_1^{\beta ve} , and M2ve M_2^{ve} for HNN-2.
Figure 5

Graphical comparison of Mev, M1αve , M1βve , and M2ve for HNN-2.

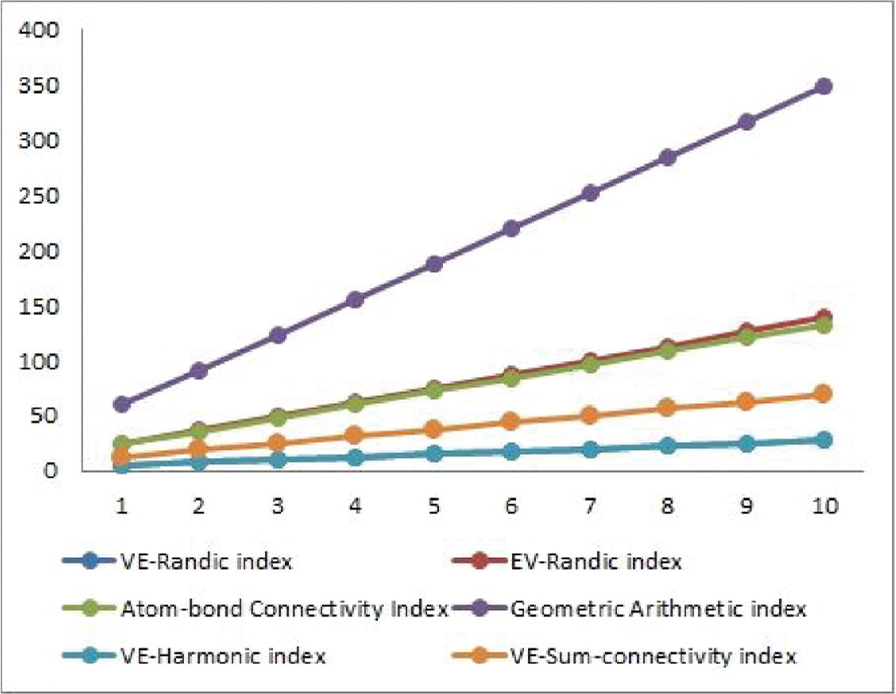
Figure 6 Graphical comparison of Rev, GAve, ABCve Hve, Rve, and χve for HNN-2.
Figure 6

Graphical comparison of Rev, GAve, ABCve Hve, Rve, and χve for HNN-2.

6 Conclusion

Research the network through graphs, topological indices are important to understand its fundamental topology. Such researches has a global utilization in the computer field science, which uses various indices based on graph invariance to deal with some provocation scenarios. In the investigation of quantitative structure-activity relationship (QSAR) and quantitative structure-property relationship (QSPR), figure invariants are important tools for approximation and predicateization the characteristics of chemical networking.

In this paper, we have presented some outcomes with respect to the edge-vertex degree and vertex-edge degree based indices such as the edge-vertex degree Zagreb and Randic indices, vertex-edge degree based First Zagreb alpha, first Zagreb beta, the second Zagreb, Randic, atom-bond connectivity (ve-𝒜ℬ𝒞), geometric-arithmetic (ve-𝒢𝒜), harmonic (ve-ℋ), and sum-connectivity (ve-χ) indices for the hierarchical hypercube network HHN −1 and HHN − 2.

Acknowledgement

Authors are grateful to anonymous referees for nice suggestion that improved the final version of the paper.

  1. Funding information:

    Authors state no funding involved.

  2. Author contribution:

    All authors contribute equally.

  3. Conflict of interest:

    Authors state no conflict of interest.

References

Al-Ayyoub A., Awwad A., Day K., Ould-Khaoua M., Generalized methods for algorithm development on optical systems. J. Supercomput., 2006, 38, 111–125.10.1007/s11227-006-7447-6Search in Google Scholar

Aslam A., Guirao J.L.G., Ahmad S., Gao W., Topological indices of the line graph of subdivision graph of complete bipartite graphs. Appl. Math. Inf. Sci., 2017, 11, 1631–1636.10.18576/amis/110610Search in Google Scholar

Baig A.Q., Naeem M., Revan and hyper revan indices of octahedral and icosahedral networks. App. Math. Nonl. Sci., 2018, 3, 33–40.10.21042/AMNS.2018.1.00004Search in Google Scholar

Bollobas B., Erdos P., Graphs of extremal weights. Ars Combinatoria, 1998, 50, 225–233.10.1016/S0012-365X(98)00320-3Search in Google Scholar

Cancan M., On edge-vertex degree and vertex-edge degree Topological Properties of Tickysim Spiking Neural Network. Comput. Intel. Neurosc., 2019, 8, 11–31.10.1155/2019/8429120Search in Google Scholar PubMed PubMed Central

Chellali M., Haynes T.W., Hedetniemi S.T., Lewis T.M., On ve-degrees and ev-degrees in graphs. Discrete Math., 2017, 340(2), 31–38.10.1016/j.disc.2016.07.008Search in Google Scholar

Chen J., Liu J., Guo X., Some upper bounds for the atom-bond connectivity indices of graphs. Appl. Math. Lett., 2012, 25, 1077–1081.10.1016/j.aml.2012.03.021Search in Google Scholar

Das K.C., Gutman I., Furtula B., On atom-bond connectivity indices. Chem. Phys. Lett., 2011, 511, 452–454.10.1016/j.cplett.2011.06.049Search in Google Scholar

Dobrynin A.A., Entringer R., Gutman I., Wiener index of trees: Theory and applications. Acta Appl. Math., 2001, 66, 211–249.10.1023/A:1010767517079Search in Google Scholar

Ediz S., Predicting some Physicochemical Properties of Octane Isomers. A Topological Approach Using ev-Degree and ve-Degree Zagreb Indices. Int. J. System Sci. Appl. Math., 2017a, 9(4), 87–94.10.20944/preprints201701.0101.v1Search in Google Scholar

Ediz S., A New Tool for QSPR Researchers: ev-Degree Randic Index. Celal Bayar Univ. J. Sci., 2017b, 13(3), 615–618.10.18466/cbayarfbe.339313Search in Google Scholar

Ediz S., On ve-degree Molecular Topological Properties of Silicate and Oxygen Network. Int. J. System Sci. Appl. Math., 2018, 9(1), 1–12.10.1504/IJCSM.2018.10011733Search in Google Scholar

Estrada E., Torres L., Rodriguez L., Gutman I., An atom-bond connectivity indices: Modelling the enthalpy of formation of alkanes. Indian J. Chem., 1998, 37, 849–855.Search in Google Scholar

Guirao J.L.G., Siddiqui M.K., Hussain A., On topological properties of block shift and hierarchical hypercube networks. Open Phys., 2018, 16, 810–819.10.1515/phys-2018-0101Search in Google Scholar

Gutman I., Polansky O.E., Mathematical Concepts in Organic Chemistry. Springer-Verlag, New York, 1986.10.1007/978-3-642-70982-1Search in Google Scholar

Gutman I., Tošoviæ J., Radenkovi S., Markovi S., On atom–bond connectivity index and its chemical applicability. Indian J. Chem., 2012, 51A, 690–694.Search in Google Scholar

Hayat S., Imran M., Computation of topological indices of certain networks. Appl. Math. Comput., 2014, 240, 213–228.10.1016/j.amc.2014.04.091Search in Google Scholar

Konstantinidou S., The selective extra stage butterfly. IEEE T. VLSI Syst., 1992, 1, 502–506.10.1109/ICCD.1992.276326Search in Google Scholar

Li Y., Li F., Zhou Z., Chen Z., SiC2 silagraphene and its one-dimensional derivatives: where planar tetracoordinate silicon happens. J. Am. Chem. Soc., 2010, 133(4), 900–908.10.1021/ja107711mSearch in Google Scholar PubMed

Sahin B., Ediz S., On ev-Degree and ve-Degree Topological Indices. Iran. J. Math. Chem., 2018, 9(4), 236–27710.20944/preprints201701.0047.v1Search in Google Scholar

Shao Z., Siddiqui M.K., Muhammad M.H., Computing Zagreb Indices and Zagreb Polynomials for Symmetrical Nanotubes. Symmetry, 2018, 10, 1–20.10.3390/sym10070244Search in Google Scholar

Wang C.F., Sahni S., Basic operations on the OTIS-Mesh optoelectronic computer. IEEE T. Parall. Distr., 1998a, 9, 1226–1236.10.1109/71.737698Search in Google Scholar

Wang C.F., Sahni S., Image processing on the OTIS-Mesh optoelectronic computer. IEEE T. Parall. Distr., 2000, 11, 97–109.10.1109/71.841747Search in Google Scholar

Wang C.F., Sahni S., Chapter 5: OTIS optoelectronic computers. In: Li K., Pan Y., Zheng S.-Q. (Eds.), Parallel Computation Using Optical Interconnection. Kluwer Academic Publishers, 1998b, 99–116.10.1007/978-0-585-27268-9_5Search in Google Scholar

Wiener H., Structural determination of parafln boiling points. J. Am. Chem. Soc., 1947, 69, 17–20.10.1021/ja01193a005Search in Google Scholar PubMed

Zhou B., Trinajstiæ N., On general sum-connectivity indices. J. Math. Chem., 2010, 47, 210–218.10.1007/s10910-009-9542-4Search in Google Scholar

Zhou L.J., Zhang Y.F., Wu L.M., SiC2 siligraphene and nanotubes: novel donor materials in excitonic solar cells. Nano Lett., 2013, 13(11), 5431–5436.10.1021/nl403010sSearch in Google Scholar PubMed

Received: 2021-03-08
Accepted: 2021-05-12
Published Online: 2021-06-18

© 2021 Nida Zahra et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. A novel approach for the production of zinc borate (4ZnO·B2O3·H2O) using a single-step hydrothermal method
  3. Fabrication, characterization, and photocatalytic performance of ternary cadmium chalcogenides CdIn2S4 and Cd7.23Zn2.77S10-ZnS thin films
  4. New cyclic and spirocyclic aminosilanes
  5. Determination of essential and non-essential element contents of drinking water and baby water for infant’s nutrition
  6. Syntheses and molecular structures of some di(amidino)monosilanes
  7. New horizons for the synthesis of nanoparticles: Germanium nanoparticles from metastable GeBr-solutions
  8. Synthesis and antimalarial activity of some triphenyltin(IV) aminobenzoate compounds against Plasmodium falciparum
  9. Coordination behavior of PPh2{C6H4[CH2N(CH2CH2)2O]-2}: Case study CdCl2[PPh2{C6H4[CH2N(CH2CH2)2O]-2}]
  10. Rapid Communications
  11. Synthesis and structure of 2,8-dimethyl-10,10-dichlorophenoxatellurine
  12. Synthesis and crystal structure of one new Pb(II) complex constructed by 1,10-phenanthroline and two carboxylate ligands
  13. Organotin(IV) selenate derivatives – Crystal structure of [{(Ph3Sn)2SeO4} ⋅ CH3OH]n
  14. Synthesis and structural characterization of a novel 2D supramolecular lead coordination polymer with phenanthroline derivate and adipic acid
  15. X-ray crystal structures of carbonate and hydroxide bridged MnII/MgII heterobimetallic complexes formed by reduction of CO2 or H2O by a Mn0–MgII bonded compound
  16. Review Articles
  17. Variable combinations of organophosphines in PtP3X derivatives: Structural aspects
  18. Tetradentate organophosphines in Pt(η4–A4L) (A = P4, P3Si, P2X2 (X2 = N2, S2, C2), PX3 (X3 = N3, N2O)): Structural aspects
  19. Special Issue: Topological descriptors of chemical networks: Theoretical studies (Guest Editors: Muhammad Imran and Muhammad Javaid)
  20. Editorial: Topological investigations of chemical networks
  21. Forgotten coindex of some non-toxic dendrimers structure used in targeted drug delivery
  22. Eccentricity based topological indices of face centered cubic lattice FCC(n)
  23. Irregular topological indices of certain metal organic frameworks
  24. Molecular topological invariants of certain chemical networks
  25. Szeged-type indices of subdivision vertex-edge join (SVE-join)
  26. Fractional metric dimension of metal-organic frameworks
  27. On topological descriptors of ceria oxide and their applications
  28. On analysis of thermodynamic properties of cuboctahedral bi-metallic structure
  29. M-polynomial-based topological indices of metal-organic networks
  30. Two modified Zagreb indices for random structures
  31. Some degree-based topological indices of caboxy-terminated dendritic macromolecule
  32. Hosoya properties of the commuting graph associated with the group of symmetries
  33. On topological properties of hierarchical hypercube network based on Ve and Ev degree
  34. On vertex PI index of certain triangular tessellation networks
  35. Some topological properties of uniform subdivision of Sierpiński graphs
https://doi.org/10.1515/mgmc-2021-0022
Keywords for this article
hierarchical hypercube network (HHN); edge-vertex degree; vertex-edge degree; molecular topological indices
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. A novel approach for the production of zinc borate (4ZnO·B2O3·H2O) using a single-step hydrothermal method
  3. Fabrication, characterization, and photocatalytic performance of ternary cadmium chalcogenides CdIn2S4 and Cd7.23Zn2.77S10-ZnS thin films
  4. New cyclic and spirocyclic aminosilanes
  5. Determination of essential and non-essential element contents of drinking water and baby water for infant’s nutrition
  6. Syntheses and molecular structures of some di(amidino)monosilanes
  7. New horizons for the synthesis of nanoparticles: Germanium nanoparticles from metastable GeBr-solutions
  8. Synthesis and antimalarial activity of some triphenyltin(IV) aminobenzoate compounds against Plasmodium falciparum
  9. Coordination behavior of PPh2{C6H4[CH2N(CH2CH2)2O]-2}: Case study CdCl2[PPh2{C6H4[CH2N(CH2CH2)2O]-2}]
  10. Rapid Communications
  11. Synthesis and structure of 2,8-dimethyl-10,10-dichlorophenoxatellurine
  12. Synthesis and crystal structure of one new Pb(II) complex constructed by 1,10-phenanthroline and two carboxylate ligands
  13. Organotin(IV) selenate derivatives – Crystal structure of [{(Ph3Sn)2SeO4} ⋅ CH3OH]n
  14. Synthesis and structural characterization of a novel 2D supramolecular lead coordination polymer with phenanthroline derivate and adipic acid
  15. X-ray crystal structures of carbonate and hydroxide bridged MnII/MgII heterobimetallic complexes formed by reduction of CO2 or H2O by a Mn0–MgII bonded compound
  16. Review Articles
  17. Variable combinations of organophosphines in PtP3X derivatives: Structural aspects
  18. Tetradentate organophosphines in Pt(η4–A4L) (A = P4, P3Si, P2X2 (X2 = N2, S2, C2), PX3 (X3 = N3, N2O)): Structural aspects
  19. Special Issue: Topological descriptors of chemical networks: Theoretical studies (Guest Editors: Muhammad Imran and Muhammad Javaid)
  20. Editorial: Topological investigations of chemical networks
  21. Forgotten coindex of some non-toxic dendrimers structure used in targeted drug delivery
  22. Eccentricity based topological indices of face centered cubic lattice FCC(n)
  23. Irregular topological indices of certain metal organic frameworks
  24. Molecular topological invariants of certain chemical networks
  25. Szeged-type indices of subdivision vertex-edge join (SVE-join)
  26. Fractional metric dimension of metal-organic frameworks
  27. On topological descriptors of ceria oxide and their applications
  28. On analysis of thermodynamic properties of cuboctahedral bi-metallic structure
  29. M-polynomial-based topological indices of metal-organic networks
  30. Two modified Zagreb indices for random structures
  31. Some degree-based topological indices of caboxy-terminated dendritic macromolecule
  32. Hosoya properties of the commuting graph associated with the group of symmetries
  33. On topological properties of hierarchical hypercube network based on Ve and Ev degree
  34. On vertex PI index of certain triangular tessellation networks
  35. Some topological properties of uniform subdivision of Sierpiński graphs
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 20.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/mgmc-2021-0022/html
Scroll to top button