Abstract
Rubin, Hannah, and Cailin O’Connor (2018. “Discrimination and Collaboration in Science.” Philosophy of Science 85 (3): 380–402) introduced a game-theoretic model to examine the dynamics of collaboration and discrimination in academia. They found that small minority groups face higher rates of discrimination in collaboration, despite moral and legal demands for equality. This paper extends their work by assessing the effectiveness of anti-discrimination measures, focusing on German legal provisions for discrimination in the workplace: internal complaints boards and training and organisational measures as mandated by the General Equal Treatment Act. My results show that internal boards are effective in preventing discrimination in initially fair (i.e. non-discriminatory) environments, but fall short in already discriminatory environments. In contrast, training and organisational measures significantly reduce discriminatory behaviour, even where awareness is low. This highlights the importance of proactive anti-discrimination measures.
1 Introduction
Philosophers of science have long used formal frameworks such as agent-based models to show how structuring communication and collaboration can have a significant impact on the scientific enterprise (see, for example, Zollman 2007; Zollman 2010; Mayo-Wilson, Zollman, and Danks 2013; Grim et al. 2015; Holman and Bruner 2015; Rosenstock, O’Connor, and Bruner 2017). One insight from this body of work suggests that maintaining a diversity of beliefs within an epistemic community is essential for the group to eventually converge on an accurate understanding of the world (Zollman 2010). At the same time, feminist philosophers of science have argued that personal diversity, including variations in gender, race, and cultural background, serves as an important source for fostering such epistemic diversity (see, for example, Haraway 1989; Longino 1990; Harding 1991).
This literature has prompted research into the factors that influence or potentially undermine the diversity of collaborative networks. Bruner (2019) demonstrated that in interactions between diverse social groups, where one group has majority status and the other is in the minority, the minority group is often disadvantaged in situations involving repeated bargaining and resource allocation (such as determining the order of authorship in a collaborative paper). This is because minority agents are statistically more likely to encounter majority agents, simply because of the size advantage of the majority group. Consequently, in negotiation scenarios, minority agents often make modest demands to avoid the consequences of unsuccessful negotiations. Over time, this leads to minority agents making smaller demands, which in turn teaches majority agents that they can take advantage of the minority by making unfairly high demands.
Rubin and O’Connor (2018) and O’Connor and Bruner (2019) have further analysed this effect in the context of academic collaboration. Using evolutionary game theory methods, they found that small minority groups, such as female scientists, are likely to be discriminated against in collaborations. This occurs despite the assumption that majority and minority agents are equally competent in terms of knowledge and skill levels, and are not inherently biased (e.g., sexist). Rubin and O’Connor (2018) also studied the co-evolution of discrimination and collaboration, observing the emergence of partially segregated networks in which some agents adhere to discriminatory behaviours. These findings suggest that discrimination in science could potentially reduce diversity in collaborative networks.
To understand these findings, we first need to clarify what we mean by ‘discrimination’ or ‘discriminatory behaviour’. The concept of discrimination is inherently complex and nuanced, with no universally accepted definition in the legal and political spheres (Edwards and Vandenhole 2007, p. 33). For example, neither the International Covenant on Civil and Political Rights nor the European Convention for the Protection of Human Rights provide a clear definition of discrimination, instead offering a non-exhaustive list of prohibited grounds, such as sex, race, or political opinion. As a general approximation, discrimination can be characterised as behaviour and policies that place individuals at a comparative disadvantage due to their membership in a particular social group (Altman 2020, Section 1.1).[1] In the context of a collaboration network, discrimination manifests as behaviour in which agents treat members of their own social group and those from different social groups differently, to the disadvantage of minority group members. In bargaining and resource allocation, discrimination thus involves the practice of distributing resources unequally based on factors such as gender, race, or other social group characteristics (Epstein 2012, p. 177).
Not only may discrimination negatively affect the ability of collaborative networks to arrive at true beliefs, as shown e.g., by Rubin and O’Connor’s work, but the dominant position in philosophical, political, and legal discourse is that discrimination is morally reprehensible and should be legally prohibited in many contexts (Altman 2020). In fact, the vast majority of countries around the world have either constitutional or legislative measures prohibiting discrimination (Porat 2005). In this paper, I focus on German law as an example of how anti-discrimination measures can be embedded within a country’s constitution and legislation. The German constitution (Grundgesetz) calls for the equality of all people and explicitly prohibits any form of discrimination. In particular, it affirms the equal rights of men and women and obliges the state to promote the realisation of these rights and to work towards the elimination of existing disadvantages (Grundgesetz, Article 3 (2)). The General Equal Treatment Act (Allgemeines Gleichbehandlungsgesetz) further elaborates on anti-discrimination measures, particularly in the area of working life and, by extension, within the academic sphere.
Given the specific understanding of discrimination described above and Rubin and O’Connor’s findings on the impact of discrimination on academic collaboration, my aim in this paper is to study whether current anti-discrimination measures, as specified in the General Equal Treatment Act, can effectively prevent and stop discrimination in collaboration networks. To assess this, I extend Rubin and O’Connor’s game-theoretic framework to model two current anti-discrimination measures. I examine a) the impact of an internal complaints board to which agents can turn if they experience or observe discriminatory behaviour, and b) the impact of training and organisational measures that help employers identify discrimination in their organisation. My game theoretic model shows that the existence of an internal complaints board is an effective means of preventing discrimination in an initially non-discriminatory society. However, in the case of an initially discriminatory environment, even though discriminatory behaviour is still reduced, the establishment of an internal complaints board is no longer sufficient to effectively stop discrimination. Compared to an internal complaints board, I show that training and organisational measures are much more effective in preventing and stopping discriminatory behaviour, even in environments where there is little or no general awareness of discrimination.
This paper proceeds as follows. In Section 2 I describe the Nash demand game that Rubin and O’Connor (2018) use as the basic model to explain discrimination in academic collaboration. Section 3 then presents how discrimination emerges in Rubin and O’Connor’s model. Following this, I describe two anti-discrimination measures (Section 4) and how they are modelled in the game-theoretic framework (Section 5). Section 5 also shows the results for the different measures. Finally, Section 6 summarises the main findings, discusses the relevance of these results and presents some open research questions.
2 Bargaining and Discrimination
Rubin and O’Connor (2018) have presented a model to study the evolution of discrimination in collaborative networks.[2] Their analysis focuses on academic settings and is motivated by the Matilda effect in academia: The persistent undervaluation of women’s contributions to science in favour of their male collaborators (Lincoln et al. 2012; Rossiter 1993).[3] For example, West et al. (2013) found that women were much less likely to be listed as first or last author, the most prestigious author positions, on a paper (see also Larivière et al. 2013). This finding is also supported by Feldon et al.’s (2017) study, which showed that while female PhD students in biology worked significantly more hours, their male counterparts were 15 % more likely to receive authorship of the journal articles they produced. In summary, these studies suggest that women receive less credit than men for collaborative work, and are persistently under-recognised.
Rubin and O’Connor’s aim is to explain this finding using an evolutionary game-theoretic model. Evolutionary game theory provides a structured framework for analysing the evolution of group behaviour in strategic interactions over time. Originally developed to explain the dynamics of natural selection, it was quickly adopted by researchers across the social sciences to understand cultural learning in humans (Alexander 2021). This framework is particularly suited to studying the topic of interest because it addresses strategic situations such as collaboration and negotiation, where each participant’s outcome is shaped by the actions of others. Moreover, behaviour in these scenarios evolves through individual experience of past interactions, suggesting a systematic change over time, which is well suited to evolutionary analysis.
Evolutionary game theoretic models are, not surprisingly, built around a game, which is a simplified representation of the interaction between agents (often referred to as players). It is defined by a set of players, a set of strategies for each player, the information each player has during the game, and the possible payoffs for each possible combination of strategies chosen. To represent the specific case of academic collaboration and the associated division of labour and credit, Rubin and O’Connor (2018, p. 382) use the Nash demand game (Nash 1950).
In this game, two agents have the opportunity to share a resource. To do this, they simultaneously state their desired share, i.e. the agents only learn of the other agent’s request after they have stated their own. If the requests are compatible, each agent gets what they asked for. If their demands are incompatible, i.e. they exceed the available resource, the agents receive a bad payoff. Thus, the Nash demand game is characterised by mutual gain when agents cooperate. Table 1 shows the payoffs for this game, given that agents can make three different demands – low (L), medium (M) and high (H).
A payoff table for a mini Nash demand game. The total resource is 10. Both players can make a low (1–4), medium (5) or high (6–9) demand. The rows show the possible strategies for Player 1. The columns show the possible strategies for Player 2. The corresponding payoffs are listed first for Player 1 and then for Player 2.
| Player 2 | ||||
|---|---|---|---|---|
| Low L | Medium M | High H | ||
| Low L | L, L | L, 5 | L, H | |
| Player 1 | Medium M | 5, L | 5, 5 | 0, 0 |
| High H | H, L | 0, 0 | 0, 0 | |
According to Rubin and O’Connor (2018, pp. 382, 383), the Nash demand game is a useful model of academic collaboration because it captures two key features of collaboration. First, academic collaboration involves joint action, which generates more recognition than solo work. Second, this joint action requires two different types of bargaining: The agents have to agree both on who contributes how much to the project and on who gets which position in the list of authors of the paper at the end. Consequently, we can think of the demands in the game as requests for author positions in relation to the actual work contributed. Someone who does most of the work and claims first authorship in return makes a medium claim M. In contrast, someone who puts in more effort but only asks for co-authorship will make a low request L. Finally, someone who contributes little to the project but still claims second authorship makes a high demand H.[6]
Now consider a population that is divided into two social groups – for example, women and men.[7] In addition, we assume that agents can condition their strategy on the group membership of the agent with whom they interact. For example, male agents may adopt a different strategy when interacting with male (in-group) and female (out-group) agents. Agents then play the Nash demand game repeatedly and may change their strategy to optimise their expected payoff. Thus, the proportion of a population playing a particular strategy will change as a function of how successful that strategy is for those playing it. In particular, a strategy that is more successful than average will proliferate in a population, and one that is less successful will be crowded out.
As a result, different norms may emerge within and between groups. I here follow Rubin and O’Connor (2018, p. 383, footnote 7) in understanding norms as emerging patterns of behaviour at the group level.[8] Three different norms could be established between the two social groups. Either the groups learn to make medium demands M from each other, or one group learns to always make high demands H and the other learns to always make low demands L. According to Epstein (2012, p. 177), these latter types of outcomes represent discriminatory norms. Agents treat in-group agents (i.e., members of their own social group) and out-group agents (i.e., members of another social group) differently, harming out-group members. In contrast, an equity (Epstein 2012, p. 177) or fair (Rubin and O’Connor 2018, p. 383) norm is one that does not discriminate.
3 The Emergence of Discriminatory Norms
Using the general framework described in the previous section, Rubin and O’Connor (2018) have built a computational model of academic collaboration networks. In what follows, I first reconstruct their model, originally programmed in the matrix-based software MATLAB, in NetLogo. This model will serve as the basis for my own analysis, which I will turn to in Section 5.
Netlogo is an open source programming language that comes with an integrated development environment (IDE) and is explicitly designed for agent-based modelling (ABM). An ABM consists of a number of independent decision-making agents. Each agent evaluates their situation and decides what to do based on a set of rules (Bonabeau 2002, p. 7280). In addition, the agents repeatedly interact with each other. In the model I am going to study, the agents represent the scientists of an academic community and belong to two different social groups (men or women). One of the social groups (women) constitutes a minority of the total population. Collaboration, on the other hand, is represented by links: The presence of a link between two agents means that they collaborate. Conversely, agents that are not connected by a link do not collaborate. Furthermore, I distinguish between in-group links, which connect agents belonging to the same social group, and out-group links, which connect agents with different social identities. In particular, each agent has a probability pin of forming an in-group link and a (possibly different) probability pout of forming an out-group link. Finally, agents randomly choose an initial strategy for the Nash demand game. Their strategy can be either low (L), medium (M) or high (H). Moreover, they can have different strategies for in-group and out-group members, i.e. their strategy can be conditioned on the social identity of their collaborator. Importantly, however, Rubin and O’Connor’s model does not assume that agents are inherently sexist or more generally biased. The initial network is therefore norm-free (Epstein 2012, p. 177) and the agents’ only goal is to maximise their payoff in the game.
After this initial setup of the network, the agents repeatedly interact with their collaborators. In each round, the agents play the Nash demand game against all their collaborators and, with some small probability, decide to change their strategy using the myopic best response. This updating can again be conditioned on the group memberships of the collaborators and is based solely on the payoffs the agent receives from interacting with their collaborators: The strategy the agent will use in the next round is the one that would have given them the highest payoff in this round, given their collaborators’ current strategies.[9] This updating rule reflects the fact that the agents seek to maximise their payoffs, i.e. they want to choose a strategy that promises the highest possible payoff in a successful collaboration, while avoiding the poor payoff of a failed negotiation.
Following Rubin and O’Connor, I examined “the frequencies with which populations converged to different bargaining norms” (Rubin and O’Connor 2018, p. 386) in order to quantify the emergence of a discriminatory norm in this network. Due to the probabilistic nature of the model, I counted simulation runs in which two or fewer agents played strategies that deviated from the equilibrium expectation as converged (as these agents may not have had the opportunity to adjust their strategies). I also used Rubin and O’Connor’s general parameter setting. Thus, I first assumed that agents update their strategy with a probability of 0.1 in each round.[10] Second, I ran all simulations for 1,000 rounds. Third, I changed the number of agents from 20 to 100 (with a step size of 20) and held the high H and low demand L constant at 6 and 4 respectively. Fourth, I explored scenarios where the minority group comprised 10–50 % of the total number of agents (with a step size of 10 %). Fifth, I varied the probability pout of an out-group link from 0.2 to 0.8 (in steps of 0.1), while keeping the probability pin of an in-group link constant at 0.4.[11] Sixth, I ran each parameter combination 100 times.
Within each group, the populations are very likely to converge to a fair norm of equal sharing where both agents make an medium demand M (see Figure A.1 in Supplementary Material). Even though the population also converged to a fair division between the members of the different social groups most of the time, they developed a discriminatory norm in a significant number of cases.[12] In line with Epstein’s definition (2012, p. 177), I count an agent as discriminating if they have a different strategy for in-group and out-group members and demand high H from an out-group member.
Figure 1 examines out-group strategies in more detail by showing the proportion of runs that converged to a specific bargaining norm as a function of minority size in percent.
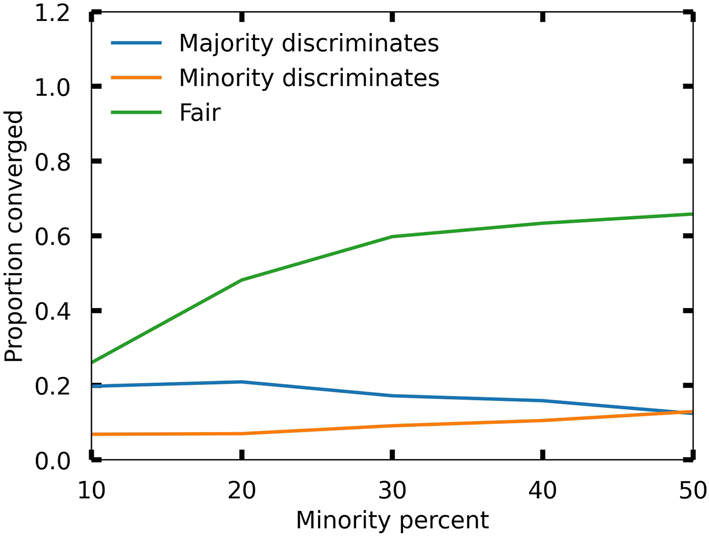
Convergence to different bargaining norms as a function of the minority size (in percent). The out-group strategies of majority and minority members are shown. The agents’ initial strategies are assigned randomly. The plots are averaged over the number of agents (between 20 and 100) and the probability pout of forming a link between two agents with different social identities (varying from 0.2 to 0.8). The high payoff H was held constant at 6.
The blue line represents the proportion that converged to a discriminatory norm where the majority discriminates against the minority, i.e. the majority members play high against the minority members and the minority members play low against the majority members. The orange line displays the opposite case, where the minority discriminates against the majority. Finally, the green line shows the results for a fair split between minority and majority agents. For a small minority, the majority is more likely to make a high demand H and thus discriminate against the minority. As the size of the minority increases, a fair division between majority and minority agents corresponding to a medium demand M becomes more likely. Furthermore, the figure indicates that both groups become equally likely to discriminate as the minority size approaches 50 % of the total population.
The observed presence of discriminatory norms when the minority size is small is a consequence of the imbalance in the average number of links (collaborators) for each group (see also Ventura 2023). Consider the following example of a population with 10 majority and 5 minority members.[13] The network is characterised by 10 out-group links. Thus, on average, a majority agent has one out-group link, while a minority agent has two. For the majority agent, each strategy (low, medium and high) is equally likely to be their best out-group response. In contrast, for the minority agent, both of their collaborators would have to demand 4 for their best response to be 6. Since the strategies are initially randomly assigned, the initial probability of this is (1/3) ∗ (1/3) = 1/9. On the other hand, only one of their collaborators would have to demand 6 for their best response to be 4. Again, since the initial network is random, this happens with probability (1/3) ∗ (1 + (1/3) + (1/3)) = 5/9. Thus, in the beginning, a minority agent is significantly more likely to demand 4 and significantly less likely to demand 6 than a majority agent. Over time, populations are driven to a state where the majority demands high, and minorities tend to be discriminated against in collaboration.
4 Anti-Discrimination Measures
In the previous section, we saw that minority groups are more likely to be discriminated against in collaboration networks. In particular, once a discriminatory norm has been established, i.e. majority members discriminate against minority members, the majority members never stop their discriminatory behaviour (see Figure A.2 in Supplementary Material). This illustrates that minority members have no chance of improving their situation without additional measures. However, the prevailing consensus in philosophical, political, and legal discourse is that discrimination is morally wrong and should be legally prohibited in many contexts (Altman 2020). Indeed, the vast majority of countries worldwide have adopted constitutional or legislative measures to prohibit discrimination (Porat 2005).
In this paper, I focus on legal protections against discrimination in Germany as an example of how such measures can be implemented at the national level. Germany’s approach is particularly illustrative due to its strong constitutional commitment to equality and its comprehensive legislative framework.[14] In Germany, the equality of all people before the law is enshrined in Article 3 of the German Basic Law (Grundgesetz). In particular, Article 3 (2) states: “Men and women shall have equal rights. The state shall promote the actual implementation of equal rights for women and men and take steps to eliminate disadvantages that now exist.” Protection is further codified in the General Equal Treatment Act (Allgemeines Gleichbehandlungsgesetz, AGG). It explicitly prohibits discrimination in the world of work, which includes academia, and aims to prevent and end discrimination (Federal Anti-Discrimination Agency 2019, p. 9). I will focus on two anti-discrimination measures described in the AGG and briefly introduce each of them below.
4.1 Internal Complaints Board
Employers have the right to file a complaint if they are experiencing any form of discrimination in the workplace, either with the relevant office within the company (internal complaints board) or with a state institution (Federal Anti-Discrimination Agency, 2019, p. 28; see also Section 13 of the AGG). Employers are required by law to set up such internal complaints boards (Federal Anti-Discrimination Agency 2019, p. 28). The complaint must be properly investigated and the outcome communicated to the complainant (Federal Anti-Discrimination Agency 2021). To stop the discriminatory behaviour, employers can take “measures such as reprimands, reassignment, transfer or dismissal” (Federal Anti-Discrimination Agency 2019, p. 28).
4.2 Training and Organisational Measures
The AGG requires employers to make their employees aware of the illegality of discrimination and to ensure that discrimination does not take place in their company (Federal Anti-Discrimination Agency 2021). One-to-one interviews, internal or external training, continuing education and staff meetings are some examples of how this can be done (Federal Anti-Discrimination Agency 2021). Employers must also protect their employees from discrimination by third parties (Federal Anti-Discrimination Agency 2019, p. 27). Works and staff councils also have a duty to promote anti-discrimination measures (Federal Anti-Discrimination Agency 2019, p. 27).
5 The Effect of Anti-Discrimination Measures on the Evolution of Discrimination
In Rubin and O’Connor’s (2018) setup, agents’ strategies are known only to themselves. The only time an agent learns about the current strategy of another agent is during the Nash demand game: Both agents simultaneously state their demand, thereby informing the other agent of their current bargaining strategy. If both agents belong to the same social group, they learn the other agent’s current in-group strategy; otherwise, they learn the other agent’s current out-group strategy. Therefore, in Rubin and O’Connor’s setup, agents are never in a position to judge whether another agent’s behaviour is discriminatory (since they learn either an agent’s current in-group strategy or out-group strategy, but never both). In what follows, I relax this assumption. Collaboration with other people is always embedded in a social network, where other collaborators or the employer may notice discriminatory behaviour. Both of the anti-discrimination measures I presented in the last section make use of this fact.
In this section I will discuss both anti-discrimination measures in turn. For each of them, I will first explain how I model them within Rubin and O’Connor’s game theoretic framework, and then show how they affect discriminatory behaviour in a collaboration network. For both measures, as in Section 3, I consider a collaboration network consisting of two different types of agents (e.g., men and women) in which one social group (e.g., women) is in the minority. The agents then repeatedly play a Nash demand game and update their strategy with small probability by calculating their expected payoffs (see Section 2 for details). Since an agent’s learning, and hence the convergence of a network to a particular bargaining norm, depends solely on their (expected) payoff in the Nash demand game, I model all anti-discrimination measures as changes in the payoff matrix. Furthermore, I examine the effects of the measures both on initially non-discriminatory networks (i.e., the initial strategies are randomly assigned) and on initially discriminatory networks where the majority demands high and the minority demands low at the beginning of the simulation.
5.1 Internal Complaints Board
To model the existence of an internal complaints board within an institution, I assume that in each round of the Nash demand game, the agent’s strategies become known to one (in-group or out-group) collaborator. For example, we could imagine that the agent works more closely with this collaborator because they are both responsible for a particular project. Due to this close collaboration, the collaborator sees how the agent treats their other (in-group and out-group) collaborators. I further assume that only if the collaborator is non-discriminatory[15] themselves they recognise whether the agent shows discriminatory behaviour. If this is indeed the case, the collaborator will, with some probability p c , report the agent to the responsible office.[16]
I introduce this probability of reporting p c as studies have found that both people who themselves experience discrimination or harassment on the basis of gender, race and other protected classes and people who witness such harassment often do not file a complaint (Suff 2020; Rai and Agarwal 2017). For example, victims of discrimination may decide not to report an incident because they fear that their complaint will not be taken seriously or that they will be blamed and ridiculed (Zheng 2020). Witnesses of discrimination, on the other hand, may fear that the perpetrator will retaliate against them, for example by passing them over for promotions or by giving them negative performance reviews (U.S. Equal Employment Opportunity Commission n.d.). For simplicity, I will also assume that an agent who has been reported to the internal complaints board is certain to be punished. The punishment is a payoff of 0 for the current round.[17]
In this section, agents repeatedly engage in the Nash demand game with all their collaborators, as outlined in Section 3. To remain consistent with Rubin and O’Connor’s (2018) work, I use the same updating rule as they do: agents update their strategies with a probability of 0.1 in each round, using myopic best response. This specific updating rule offers an additional advantage in the context of my work: it avoids introducing a bias towards fair, non-discriminatory behaviour. Specifically, agents treat poor payoffs resulting from punishment due to discriminatory behaviour as salient events but do not disproportionately emphasise them relative to the high payoffs they receive when their discriminatory behaviour goes undetected. Moreover, myopic best response offers practical advantages: it has a low computational cost and minimal memory requirements compared to other updating rules, such as fictitious play or rational learning (Izquierdo, Izquierdo, and Vega-Redondo 2012). The update probability of 0.1 is motivated by empirical evidence that people have a strong tendency to stick to their last behavioural choice (even for unethical behaviour), and that this tendency is even more pronounced than adjusting behaviour using myopic best response (Alós-Ferrer, Hügelschäfer, and Li 2016; Erev and Haruvy 2020; Zhang, Cornwell, and Higgins 2014).
Finally, an agent’s updating procedure relies solely on the payoffs they receive from interactions with their collaborators, as in Section 3. The strategy selected for the next round is the one that would have yielded the highest payoff in the current round. However, unlike the previous section, the expected payoff now depends not only on the current strategies of the collaborators but also on the anti-discrimination measure. This measure modifies the original payoff table (Table 1), replacing it with Table 2 for any discriminating agent reported to the internal complaints board in the current round.
The payoff table in the mini Nash demand game for a discriminatory agent (Player 1) who has been reported to the internal complaints board. The total resource is 10. Both players can make a low (4), medium (5) or high (6) demand.
| Player 2 | ||||
|---|---|---|---|---|
| Low L | Medium M | High H | ||
| Low L | L | L | L | |
| Player 1 | Medium M | 5 | 5 | 0 |
| High H | 0 | 0 | 0 | |
However, if an agent is not reported to the internal complaints board in the current round, their expected payoff continues to be determined by the original payoff table (Table 1). The probability of a discriminatory agent being reported is based on the ratio of non-discriminatory collaborators to total collaborators, as well as the probability p c (see the description of the anti-discrimination measure in the model above for details). Agents who do not engage in discriminatory behaviour are unaffected by the anti-discrimination measure, so their payoffs remain the same as in the original payoff table (Table 1).[18]
In order to quantify how the anti-discrimination measure affects the evolution of the discriminatory norm, I again examine the frequency with which populations converge to different bargaining norms (see p. 9). As in Section 3, agents updated their strategy with probability 0.1 in each round, and all simulations were run for 1,000 rounds. The number of agents was varied from 20 to 100 (with a step size of 20). The high demand H and the minority size were fixed at 6 and 20 %, respectively. Figure 2 shows how the presence of an internal complaints board affects the convergence of the population to different bargaining norms, i.e. it plots the proportion of converged runs as a function of the probability p c of being reported by a collaborator.[19]
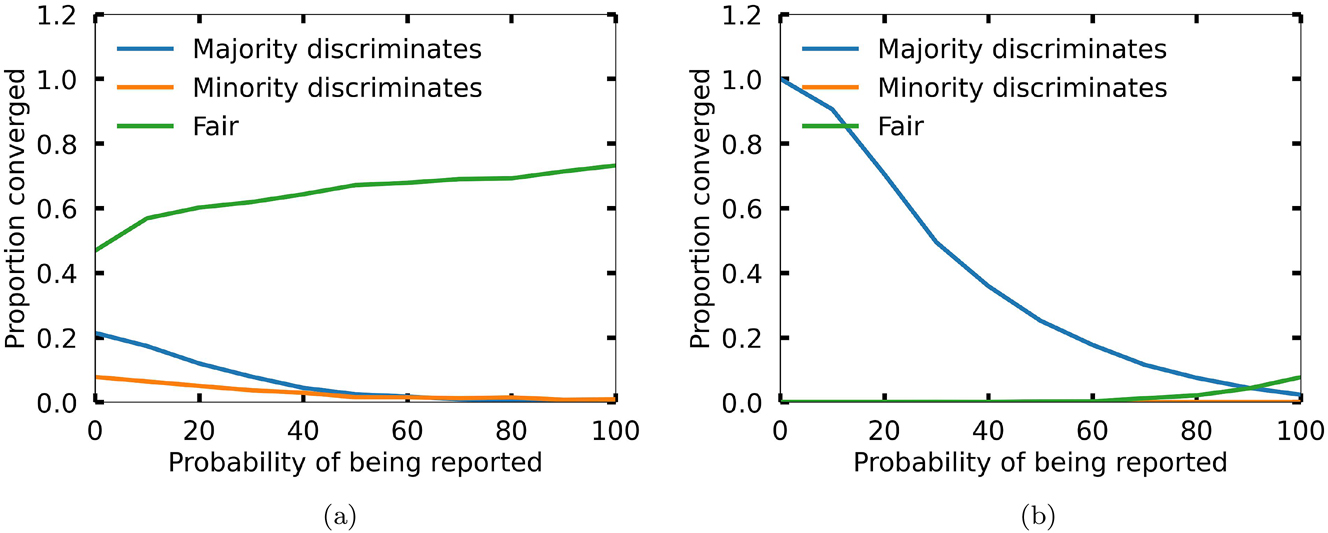
Convergence to different bargaining norms as a function of the probability p c of being reported by a collaborator if the anti-discrimination measure of an internal complaints board is applied. The out-group strategies of majority and minority members are shown. Initially, the out-group strategies are either (a) assigned randomly or (b) discriminate against the minority. The plots are averaged over the number of agents (between 20 and 100) and the probability pout of forming a link between two agents with different social identities (varying from 0.2 to 0.8). The high payoff H and the minority size (in percent) were held constant at 6 and 20 %, respectively.
Figure 2a presents the results for an initially non-discriminatory society in which the strategies for the Nash demand game are randomly assigned, while Figure 2b illustrates the data for an initially discriminatory society in which all majority members make high demands when playing against minority members and all minority members make low demands when playing against majority members. For both initial networks, as the probability p c increases, the population converges more and more towards a fair norm. If the initial distribution of strategies is random, the population is most likely to end up in a state of fair division. At a low value of p c = 10 %, the proportion of runs converging to the discriminatory norm, where the majority discriminates against the minority, is slightly below 0.2 and decreases to nearly 0 as p c approaches 100 %. In particular, the proportion of runs converging to a discriminatory norm falls below 0.06 for p c greater than 40 %. If p c is even higher, the proportion where the majority discriminates against the minority drops below 0.01. Without any anti-discrimination measure, the proportion of runs converging to a discriminatory norm is significantly higher, namely 0.21 (see Section 3, Figure 1). Conversely, the fair norm starts at about 0.55 when p c = 10 % and increases steadily to about 0.7 when p c reaches 100 %. The norm where the minority discriminates against the majority remains negligible throughout, hovering close to 0.
The reason why the population is less likely to converge to a discriminatory norm is that the measure makes it less attractive for majority agents to make a high demand H when playing against minority members. As a simple example, consider a majority agent who is currently behaving discriminatorily. Suppose further that they have one (non-discriminatory) out-group collaborator who is currently making a low demand L. In the absence of any anti-discrimination policy, the agent’s best response is to play high,[20] since this strategy yields the highest expected payoff (namely a payoff of 6). However, if the anti-discrimination measure is in place, the collaborator will report discriminatory behaviour with probability p c . If the majority agent is indeed reported to the internal complaints board, their expected payoff for playing high changes from 6 to 0, and playing medium, resulting in a payoff of 5, becomes the best strategy. Over time, therefore, majority agents learn to play fairly against minority members, and minority members are consequently less likely to end up discriminated against. The simulation thus shows that the existence of an internal complaints board is an effective means of preventing discrimination in an initially non-discriminatory society.
However, if the initial distribution of strategies is discriminatory (Figure 2b), in most cases the population converges to a norm where the majority continues to discriminate against the minority (unless the probability p c is above 90 %). At a low probability of being reported p c = 10 %, the proportion of runs converging to a society where the majority discriminates against the minority is close to 0.9, indicating almost complete convergence to discrimination. As p c increases, this proportion gradually decreases, but is still around 0.1 even at p c = 80 %. The fair norm, on the other hand, starts very low at almost 0.0 at p c = 10 % and does not exceed the norm with majority agents showing discriminatory behaviour until p c reaches about 90 %, eventually rising to about 0.1 at p c = 100 %. Minority discrimination remains minimal, similar to the case of a random initial distribution of strategies.
This effect results from the complete dominance of discriminatory behaviour in the initial society. Since I assume that agents who discriminate themselves do not report discriminatory behaviour (e.g., due to a lack of awareness), the only possibility is that the discriminatory agent is reported by a member of the minority. However, as the minority represents only 20 % of the population, this is very unlikely. Consider a simple illustrative example where the probability of being reported by a collaborator is set to p c = 40 %. Suppose a discriminatory majority member has two in-group links and one out-group link. If both of their in-group members are non-discriminatory, then the probability that their discriminatory behaviour will be noticed and reported to the internal complaints board is 0.4 ∗ (1/3 + 1/3 + 1/3) = 0.4. If, on the other hand, the agent’s in-group collaborators are themselves discriminatory agents, this probability is lowered to 0.4 ∗ 1/3 = 0.13.
This simple example illustrates that an initially discriminatory network reduces the number of agents who have the general awareness to notice discrimination and thus reduces the number of agents who might report discriminatory behaviour to the internal complaints board. As a result, discriminatory agents are less likely to be reported and therefore less likely to stop their discriminatory behaviour in favour of a fair strategy. Consequently, although discriminatory behaviour is reduced compared to a situation without anti-discrimination measures (see Figure A.2), the measure of establishing an internal complaints board does not seem sufficient to effectively stop discrimination in an initially discriminatory society.
Figure 2 reveals another interesting point, namely that the number of runs that converged to a fair norm is very low compared to Figure 1, especially in the case of an initial discriminatory distribution of strategies as shown in Figure 2b. One hypothesis why this might be the case is that in an initially discriminatory society it takes a long time to unravel discrimination. A discriminatory majority agent needs to be first reported to the initial complaints board by either a discriminated minority agent or a non-discriminatory majority agent and must subsequently update their strategy accordingly which happens with probability 0.1.
To address this point, I conducted additional simulations with an extended duration of 10,000 rounds, compared to the original 1,000 rounds. These simulations were performed for both an initial random distribution of strategies and an initially discriminatory distribution and can be found in Figure A.4 in Supplementary Material. The results showed that extending the simulation time did not significantly increase the proportion of runs converging to a fair norm. Specifically, the change was less than 0.09 % for both initial conditions, suggesting that the original simulation duration was sufficient.
This outcome implies that rather than a delay in convergence, the model may not reach a stable equilibrium where one strategy consistently dominates. In other words, while the internal complaints board may reduce discrimination to some extent, it may not be sufficient to establish a stable social norm of fairness. Two assumptions of my model are likely to contribute to this: First, agents in the model update their strategies based on a myopic best response, considering only the outcome of the Nash demand game from the current round. Second, the anti-discrimination measure implemented is a one-time intervention, penalising agents only in the round where discrimination is observed and reported.
For instance, consider a majority agent with one minority collaborator. If the minority agent demands low, the majority agent’s optimal response is to demand high. However, if the majority agent’s discriminatory behaviour is observed and reported by a non-discriminatory agent, they will receive a poor payoff and shift to a medium demand strategy. Given the myopic strategy updates, the agent may end up oscillating between making high and medium demands, depending on whether their behaviour has been reported in the current round. This cyclical pattern could explain the limited convergence to a fair norm. Although the current model setup only allows for the analysis of the final state after 1,000 rounds, future research could examine the temporal evolution of strategies to determine whether such cyclical behaviour indeed occurs.
So far, I have explored two initial distributions of strategies: one where strategies are randomly assigned, and another where all majority agents discriminate against the minority. However, neither of these scenarios fully reflects realistic conditions. To address this, and following Schneider, Rubin, and O’Connor (2022), I examined an additional initial distribution of strategies that represents a more nuanced, mixed scenario in the Nash demand game, where only some majority agents exhibit discriminatory behaviour from the outset.
This mixed case is intended to capture two key aspects of discrimination and the measures implemented to combat it. First, as discussed in Section 2, minorities often receive fewer benefits from collaboration in real academic communities. Second, anti-discrimination measures tend to be introduced in societies where some degree of discrimination already exists. To account for these dynamics, I adjust the initial probabilities of out-group strategies. Specifically, there is a 45 % probability that a majority group member will demand a high payoff when interacting with a minority group member, and a 45 % probability that a minority group member will demand a low payoff when interacting with a majority group member. The remaining strategies are given equal probability. While these probabilities are somewhat arbitrary, they are designed to represent a scenario where discrimination is already embedded in the community (see Schneider, Rubin, and O’Connor 2022). The results of this setup are illustrated in Figure 3.
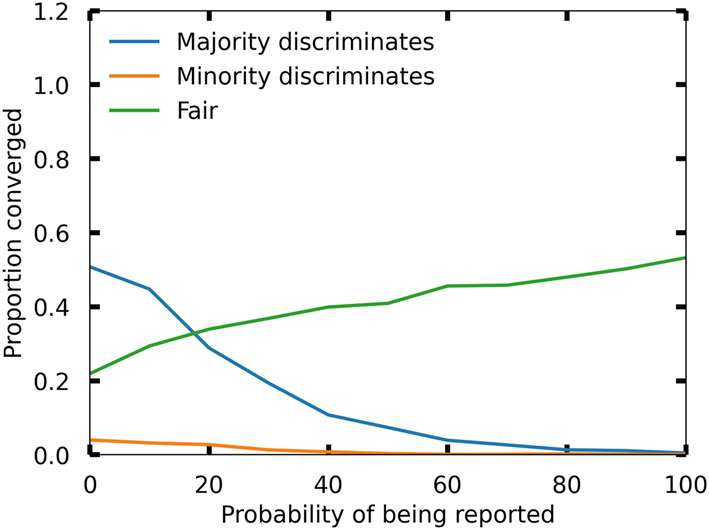
Convergence to different bargaining norms as a function of the probability p c of being reported by a collaborator if the anti-discrimination measure of an internal complaints board is applied. The out-group strategies of majority and minority members are shown. Initially, the out-group strategies are assigned such that there is a 45 % probability that a majority agent discriminates against the minority. The plots are averaged over the number of agents (between 20 and 100) and the probability pout of forming a link between two agents with different social identities (varying from 0.2 to 0.8). The high payoff H and the minority size (in percent) were held constant at 6 and 20 %, respectively.
As the figure shows, the fair norm gradually gains traction as p c increases, although the rate of adoption is slower than when strategies are initially randomly assigned. At the same time, the proportion of runs in which the majority discriminates against the minority also decreases, but this decrease is less pronounced than in the scenario with an initial random distribution of strategies. For example, when p c = 40 %, the proportion of runs converging to a discriminatory norm is about 0.1 in the case where there is a 45 % probability that a majority agent initially discriminates against a minority agent, compared to a lower value of 0.06 in the scenario with a random initial distribution of strategies.
More generally, a comparison of Figure 3 with Figure 2 shows that the results for an initially mixed set of strategies – where some majority agents begin by discriminating against minority agents – can be understood as a superposition of the two more extreme cases: the fully random and the fully discriminatory initial distributions of strategies. In the mixed case, we see elements of both the rapid convergence to a fair norm typical of a random initial setup, and the persistence of discriminatory norms characteristic of an initially discriminatory environment. This mixture results in an intermediate scenario where the transition to fairness is neither as rapid as in the random case nor as sluggish as in the fully discriminatory case.
In summary, the internal complaints board is most effective in promoting fairness when the initial distribution of strategies is random, with a rapid decline in discriminatory norms and a rapid adoption of fair norms. Its effectiveness declines in mixed and especially initially discriminatory societies, where fair norms take longer to establish. The rate of convergence to fairness is fastest in initially non-discriminatory societies and slowest in discriminatory ones, suggesting that initial conditions influence the success of anti-discrimination measures. Discriminatory norms are most persistent in initially discriminatory societies, requiring much higher reporting probabilities p c to significantly reduce them.
5.2 Training and Organisational Measures
The various training and organisational measures are designed to make employees more aware of discriminatory behaviour. In addition, the individual interviews in particular allow employers to uncover existing discrimination in the workplace. To model these effects in a game-theoretic framework, I assume that in each round of the Nash demand game, the behaviour of the currently playing agent is controlled by the employer with probability p e . If an agent is found to have engaged in discriminatory behaviour, they will be punished. For example, they may have to undergo additional anti-discrimination training and therefore cannot continue working on their project, or they may be assigned a completely new project to protect the discriminated minority agent. In my simulation I subsume all these different types of measures by a payoff of 0 in the current round. All other parameters are set as in the last section (see p. 16).
Figure 4 illustrates how training and organisational measures affect the convergence of the population to different bargaining norms by plotting the proportion of converged runs as a function of the probability p e .[21] Figure 4a shows the results for an initially random network, while Figure 4b displays the data for an initially discriminating society. In the case of a community in which strategies are initially randomly assigned, at a low probability of inspection p e = 10 %, the proportion of runs converging to a society in which the majority discriminates against the minority is about 0.1, which decreases to 0.0 as p e increases to 100 %. In particular, even a low probability p e = 20 % almost completely prevents discriminatory behaviour. Moreover, compared to the simulation where no anti-discrimination measure is applied (see Figure 1), the measure significantly increases the proportion of runs converging to a fair norm (from 0.48 to 0.6). This proportion continues to increase with increasing probability p e , reaching slightly below 0.8 at p e = 100 %. The norm where the minority discriminates against the majority remains almost negligible throughout, staying close to 0.0.
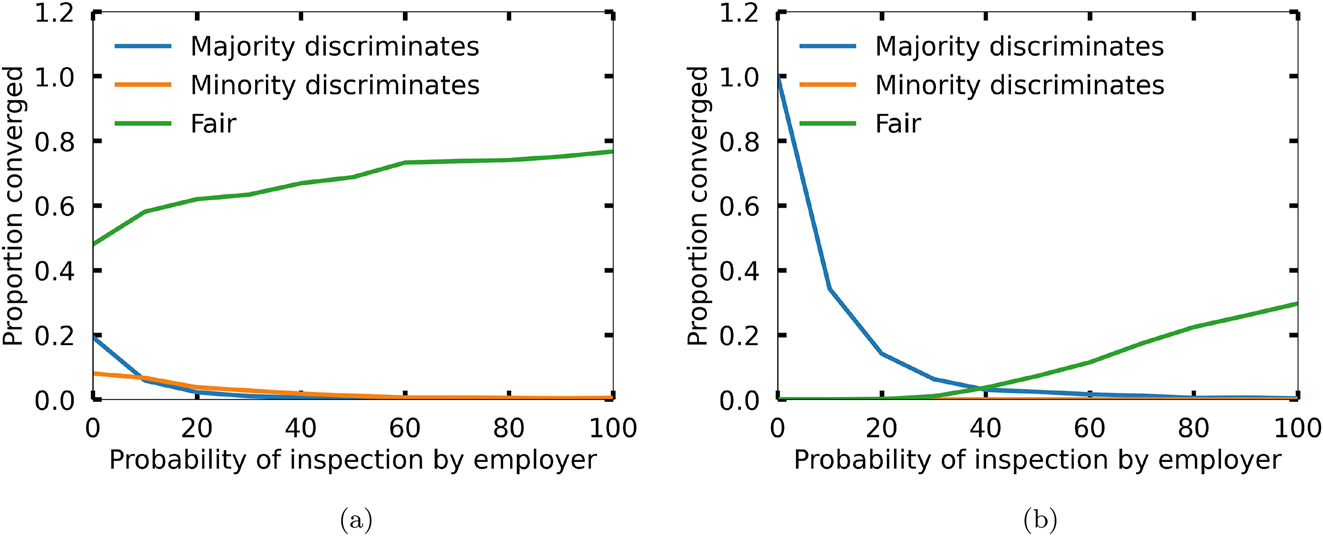
Convergence to different bargaining norms as a function of the probability p e of an inspection by the employer if training and organisational anti-discrimination measures are applied. The out-group strategies of majority and minority members are shown. Initially, the out-group strategies are either (a) assigned randomly or (b) discriminate against the minority. The plots are averaged over the number of agents (between 20 and 100) and the probability pout of forming a link between two agents with different social identities (varying from 0.2 to 0.8). The high payoff H and the minority size (in percent) were held constant at 6 and 20 %, respectively.
On the other hand, when the initial society is dominated by a discriminatory norm (Figure 4b), the measure does not stop this behaviour 14 % of the time for a probability of inspection of p e = 20 %. However, the number of runs that maintain the discriminatory norm already drops to 0.04 when the probability of control is increased to p e = 40 %. At the same time, the probability that the population will develop a fair division between majority and minority members increases, reaching 0.3 at p e = 100 %.
Similarly to the analysis in Section 5.1, I also examined the scenario where there is a 45 % probability that a majority agent initially discriminates against a minority agent. The results of this analysis are presented in Figure A.6 in Appendix A. Much like the case with the internal complaints board, the scenario with initially mixed strategies shows characteristics of the two extreme cases: one with an initially random distribution of strategies and the other with a completely discriminatory distribution. Compared to the initially random distribution, the mixed case shows a slower decline in discriminatory norms and a slower rise in fair norms, but it still performs better than the initially discriminatory distribution of strategies. This again highlights how the presence of some initial discrimination can slow the effectiveness of training and organisational measures, yet not as drastically as when the entire society is initially discriminatory.
Compared to the anti-discrimination measure of an internal complaints board (see Figure 2), the training and organisational measures analysed in this paper appear to be much more effective in preventing and stopping discriminatory behaviour. It is important to clarify that the training and organisational measures discussed here are not preventative measures applied to everyone, but rather punitive measures applied specifically after an agent has engaged in discriminatory behaviour.
The key difference between the last and this section is who is monitoring for discriminatory behaviour. In the case of the internal complaints board, the monitoring is carried out by the agent’s collaborators. As discussed earlier, a discriminatory majority agent with two in-group employees and one out-group employee faces a probability of being reported for discrimination that varies between 13 and 40 %, depending on whether their in-group collaborators are also discriminatory. In contrast, when training and organisational measures are used as a punitive response, the probability of being monitored and punished is consistently 40 %, regardless of the behaviour of the collaborators. This consistent monitoring by the employer, rather than by peers, means that training and organisational measures are effective even in environments where there is little or no general awareness of discrimination.
In summary, then, training and organisational measures, when used as a targeted punishment after discriminatory behaviour has occurred, are an effective way of preventing and stopping such behaviour.
6 Conclusions
The starting point for this paper was Rubin and O’Connor’s (2018) model for studying the evolution of discrimination in academic collaboration. Their game-theoretic framework has shown that small minority groups are significantly more likely to be discriminated against in collaboration, even when agents are not assumed to be inherently biased. Building on Rubin and O’Connor’s work, I have modelled and evaluated two different anti-discrimination measures of the German General Equal Treatment Act for the area of working life, which includes academia: a) an internal complaints board that employees can turn to if they experience or observe discriminatory behaviour, and b) training and organisational measures that allow employers to identify discriminatory behaviour in the workplace.
Both measures proved effective in preventing the emergence of a discriminatory norm in a society that was not initially characterised by discriminatory behaviour. In contrast, in a population where members of the majority were already discriminating against members of the minority, the existence of an internal complaints board was not sufficient to stop the existing discriminatory behaviour. In these cases, training and organisational measures proved to be effective in combating discrimination. In summary, my findings suggest that the current legal intervention can protect minority groups in collaboration. It is worth noting that these findings do not rely on any kind of (long-term) change in the moral beliefs of the agents. Instead, they are based on only four conditions: 1) agents condition their bargaining strategy on the social identity of their collaborator (in-group vs. out-group), 2) agents of one social identity are in the minority, 3) agents adapt their bargaining strategy to their own advantage, and 4) with some probability, the anti-discrimination measure sanctions discriminatory behaviour in the form of a single, short-term punishment.
Unfortunately, there is currently no empirical work that allows me to compare my models with empirical observations. The reports commissioned by the Federal Anti-Discrimination Agency focus heavily on the practical implementation of the General Equal Treatment Act and necessary amendments (Berghahn et al. 2016; Federal Anti-Discrimination Agency 2020; Icks et al. 2022). They provide little information about the effectiveness of different measures to prevent discrimination in academia once they are in place (Icks et al. 2022, p. 33). What they do show, however, is that universities are still struggling to implement anti-discrimination measures as required by the General Equal Treatment Act. For example, only 44 % of the universities surveyed provide anti-discrimination training (Federal Anti-Discrimination Agency 2020, p. 59). 50 % reported that they had developed policies to protect against specific forms of discrimination and 40 % that they had developed general policies to protect against discrimination (Federal Anti-Discrimination Agency 2020, p. 59). Regarding the requirement to have an internal complaints board, 58 % of the universities surveyed stated that they had such a body to which employees could complain if they felt they had been discriminated against (Federal Anti-Discrimination Agency 2020, p. 39). However, the Federal Anti-Discrimination Agency (2020, p. 9) also points out that there is no comprehensive information on the extent to which universities fulfil their obligation, as there is no monitoring.
Rubin and O’Connor’s analysis, and by extension my own, builds on West et al.’s (2013) empirical observation that women’s contributions in academia are consistently undervalued in favour of their male collaborators, as evidenced by the significantly lower likelihood of women holding prestigious author positions on published papers. My simulations examined the effectiveness of two anti-discrimination measures proposed by the German government to combat such inequalities and discrimination in the workplace. However, I did not address the enforceability of these measures in the context of collaboration inequality. Indeed, enforceability in these cases poses unique challenges. Unlike more straightforward forms of discrimination, such as pay disparities between individuals with the same qualifications but different genders, collaboration inequality involves complex social dynamics that are often difficult to quantify. The work of West et al. focuses on the gender composition of authorship in the JSTOR corpus, but does not delve into the nuances of the collaborative processes that lead to authorship decisions. As such, their study does not provide insights into the enforceability of the proposed measures in real collaborative settings. This issue highlights the need for further empirical research into the social dynamics of collaboration to better understand how anti-discrimination measures might be enforced in such contexts.
Given the current lack of data and the question of enforceability, how useful are my models? Do they have any real value?[22] Game theoretic models are remarkably simple, and thus serve only as idealised representations of complex (social) dynamics. In particular, these models assume that agents simultaneously choose their bargaining strategy, informed only by their previous experience with that strategy. In reality, situations where agents engage in continuous discussion and negotiation are likely to be more common. Another simplification is the assumption that agents learn only from personal experience and adopt strategies and behaviours that maximise their immediate utility, ignoring the myriad influences that shape human behaviour, including learning from peers and ethical considerations. Despite these simplifications, such models shed light on mechanisms within complex scenarios that would otherwise be difficult to discern. For example, the models I have presented in this paper allow us to draw the following three conclusions.
First, the results suggest that interventions such as formal complaints procedures, training and organisational measures can be effective in reducing discrimination. The findings thus provide a theoretical basis for legislators to consider adopting such measures as part of anti-discrimination policies. Second, since the anti-discrimination measures discussed in this paper only punish the discriminating agent for a single bargaining round, successful interventions can be short term. However, the effectiveness of such short-term interventions depends on the severity of the punishment. If the punishment is substantial – such as a complete loss of payoffs for the round, as modelled here – then the intervention can have a significant impact on the discriminator’s behaviour. On the other hand, if the punishment is less severe, or if the discrimination is difficult to detect, the deterrent effect may be significantly weakened. Therefore, the short-term nature of these interventions should be evaluated in the context of both the severity of the punishment and the detectability of the discriminatory behaviour. We leave the study of the interaction between these factors to future research. Third, the results highlight the crucial role of training and organisational measures in combating discrimination, especially in environments where discriminatory behaviour is highly prevalent. Where only an internal complaints board exists, the incentive for majority agents to treat minority agents fairly is very weak. This is because the likelihood of interacting with a minority agent who would then report discriminatory behaviour is often too low to act as a strong deterrent. On the other hand, training and organisational measures taken by the employer are less dependent on the behaviour of other employees. They are therefore effective even in cases where a significant proportion of the majority discriminate (assuming that the employer is sufficiently likely to notice discriminatory behaviour). My findings therefore point to the need for measures that go beyond simply enabling discrimination complaints to be made; there also needs to be wider awareness raising and proactive action by the employer to address the underlying inequalities.
In light of these findings, it seems reasonable to consider what measures the legislature could take. While my results provide a preliminary game-theoretic analysis suggesting that the anti-discrimination measures outlined in the General Equal Treatment Act can, in principle, help to prevent and stop discrimination, it is crucial to recognise the limitations of this study. The models used are highly abstract and cannot by themselves provide definitive guidance for legislative action. Instead, these findings should be seen as a starting point for further empirical research and policy discussion. On the face of it, it seems essential that legislators ensure proper implementation and enforcement of these measures, while also considering additional context-specific strategies to effectively combat discrimination in collaborative environments. I hope that my work will contribute to the ongoing discussions on how to address and prevent discrimination in collaborative settings.
Finally, I would like to point out some possible extensions of the game-theoretic framework I have used in this paper. This paper adhered to a myopic best response updating rule, where agents only consider the outcome of their most recent interactions to adjust their strategy. While this assumption is consistent with previous work by Rubin and O’Connor (2018) and reduces the computational cost of the simulations, it has inherent limitations. Agents lack the ability to consider longer-term patterns, which may underrepresent the potential for sustained behavioural change through repeated punishments and thus underestimate the effectiveness of anti-discrimination measures in promoting fairness. Future versions of the model could incorporate updating rules for longer-term memory, where punishment events have lasting effects on payoff expectations, potentially increasing the effectiveness of anti-discrimination policies. A first promising candidate is the updating rule of fictitious play (Brown 1951). A fictitious play (FP) agent acts under the assumption that each of their collaborators follows a specific mixed strategy (Izquierdo, Izquierdo, and Vega-Redondo 2012). This mixed strategy is estimated based on the observed frequencies of the collaborators’ actions up to the current point in the game. Unlike the models discussed in this paper, where agents only consider the actions taken by their collaborators in the most recent time step, FP players implicitly incorporate the entire history of the game into their updating. Once an FP player forms these frequency-based beliefs about their collaborators’ strategies, they choose their own strategy to optimally respond to these beliefs. The proposed extensions may thus provide a more nuanced understanding of the conditions under which fair strategies are likely to emerge and persist.
Furthermore, following Rubin and O’Connor (2018), the model assumed a relatively low probability of 0.1 for agents to update their strategy, reflecting slow behavioural change. While this reflects empirical evidence that people have a strong tendency to stick to their last behavioural choice (even for unethical behaviour), and that this tendency is even more pronounced than adjusting behaviour using the myopic best response (Alós-Ferrer, Hügelschäfer, and Li 2016), it makes fairness harder to achieve: For a discriminatory majority agent to switch to non-discriminatory behaviour, they must be punished just before they update their strategy. In addition, for the majority agent to maintain non-discriminatory behaviour, some of their collaborators must switch to a fair strategy before the agent’s next update opportunity, to prevent demanding high from becoming the best strategy again. Future work could therefore investigate the interplay between the updating probability and the effectiveness of anti-discrimination policies. This investigation would be particularly interesting in a model that not only considers convergent communities, as is the case in Rubin and O’Connor’s (2018), and thus my model, but also considers the dynamics of the different norms over time.
When studying the effects of an internal complaints board, I assumed that non-discriminatory employees report a discriminatory agent with some probability. If they do not report someone for discriminatory behaviour, it could be because they have not noticed it or because they are deliberately ignoring it. Importantly, the model assumes that their inaction has no negative consequences for them. They could observe or know about a discriminatory act and still choose not to say anything.[23] This tacit tolerance could represent a kind of complicity. It would therefore be interesting to investigate the effect of including a metanorm game in the simulation. This would amount to implementing a norm that punishes those who deliberately fail to report an agent who engages in discriminatory behaviour (see Axelrod 1986, p. 1101).
There is one additional measure the General Equal Treatment Act mentions but that I have not studied in this paper, namely positive measures (Federal Anti-Discrimination Agency 2010), often subsumed under the term ‘affirmative action’ in the Anglo-American world (Wladasch and Liegl 2009, p. 8). Positive measures allow employers to take targeted measures in the workplace to support groups that have been discriminated against in the past (Federal Anti-Discrimination Agency 2019, p. 28; see also Section 5 of the AGG). Proactive measures aim to eliminate, compensate for and prevent (existing) discrimination. The objective is to ensure full and effective equality of opportunity for all members of society who are disadvantaged or otherwise suffer the consequences of past or present discrimination (Federal Anti-Discrimination Agency 2010, p. 5). Positive measures are justified when a group of people is much less represented in certain contexts than in the population as a whole. An example of a positive measure is the quota, which seeks to improve the representation of women in certain areas of the workforce (Senatsverwaltung für Wissenschaft). Future work could think about how to model such positive measures within a game theoretic framework, in particular how such measures might affect the bargaining strategies of minority agents.
In this paper, I considered flat, non-hierarchical collaboration networks, i.e. the links between agents were completely randomly generated and no agent had any special role in the network. In particular, there were no interdependencies between agents. However, academic and working life in general is characterised by hierarchical structures, e.g., between a research group leader and their PhD students. Schneider et al. (2011) have found that women are still underrepresented in higher academic positions and are much more likely to leave academia than their male colleagues. The effects of this asymmetry could therefore be studied using a hierarchical network. In particular, future work could explore the circumstances under which these networks lead to discrimination and how this can be prevented. In this context, modelling and studying the effects of affirmative action seems particularly interesting. For example, a quota might increase the representation of minorities in higher positions. As a result, employees may feel more comfortable reporting discriminatory behaviour because they believe their complaint will be taken seriously. In addition, minority representatives in higher positions could support minority employees in the bargaining process with majority employees and encourage them not to accept unfair bargaining outcomes.
Acknowledgments
I would like to thank Jurgis Karpus for his invaluable feedback on earlier drafts of this paper, which have significantly enhanced its quality. I am also grateful to Ignacio Ojea Quintana for his thoughtful guidance during the review process. My thanks further go to the anonymous reviewer for their detailed comments and constructive suggestions, which have contributed greatly to the refinement of this paper. Finally, I am indebted to my supervisors, Hannes Leitgeb and Alexander Reutlinger, for their unwavering support and encouragement.
References
Alexander, J. McKenzie. 2000. “Evolutionary Explanations of Distributive Justice.” Philosophy of Science 67 (3): 490–516. https://doi.org/10.1086/392792.Suche in Google Scholar
Alexander, J. McKenzie. 2021. “Evolutionary Game Theory.” In The Stanford Encyclopedia of Philosophy, edited by Edward N. Zalta, Summer 2021 ed.. Stanford: Metaphysics Research Lab, Stanford University.Suche in Google Scholar
Alós-Ferrer, Carlos, Sabine Hügelschäfer, and Jie Li. 2016. “Inertia and Decision Making.” Frontiers in Psychology 7 (169), https://doi.org/10.3389/fpsyg.2016.00169.Suche in Google Scholar
Altman, Andrew. 2020. “Discrimination.” In The Stanford Encyclopedia of Philosophy, edited by Edward N. Zalta, Winter 2020 ed.. Stanford: Metaphysics Research Lab, Stanford University.Suche in Google Scholar
Axelrod, Robert. 1986. “An Evolutionary Approach to Norms.” American Political Science Review 80 (4): 1095–111. https://doi.org/10.1017/s0003055400185016.Suche in Google Scholar
Berghahn, Sabine, Vera Egenberger, Micha Klapp, Alexander Klose, Linda Liebscher, Dorisand Supik, and Alexander Tischbirek. 2016. Evaluation des Allgemeinen Gleichbehandlungsgesetzes. https://www.antidiskriminierungsstelle.de/SharedDocs/downloads/DE/publikationen/AGG/agg_evaluation.pdf?__blob=publicationFile&v=12 (Accessed April 27, 2024).Suche in Google Scholar
Bonabeau, Eric. 2002. “Agent-based Modeling: Methods and Techniques for Simulating Human Systems.” In Proceedings of the National Academy of Sciences, Vol. 99, 7280–7.10.1073/pnas.082080899Suche in Google Scholar
Brown, G. W. 1951. “Iterative Solution of Games by Fictitious Play.” In Activity Analysis of Production and Allocation, edited by T. C. Koopmans, 374–6. New York: Wiley.Suche in Google Scholar
Bruner, Justin. 2019. “Minority (Dis)Advantage in Population Games.” Synthese 196 (1): 413–27. https://doi.org/10.1007/s11229-017-1487-8.Suche in Google Scholar
Bruner, Justin, and Cailin O’Connor. 2017. “Power, Bargaining, and Collaboration.” In Scientific Collaboration and Collective Knowledge, edited by Thomas Boyer-Kassem, Conor Mayo-Wilson, and Michael Weisberg. New York: Oxford University Press.Suche in Google Scholar
Davaki, Konstantina. 2012. Gender Equality Policies in the USA. https://www.europarl.europa.eu/RegData/etudes/note/join/2012/462439/IPOL-FEMM_NT(2012)462439_EN.pdf (Accessed September 30, 2022).Suche in Google Scholar
Del Carmen, Alejandro, and Robert L. Bing. 2000. “Academic Productivity of African Americans in Criminology and Criminal Justice.” Journal of Criminal Justice Education 11 (2): 237–49. https://doi.org/10.1080/10511250000084891.Suche in Google Scholar
Edwards, Alice, and Wouter Vandenhole. 2007. “Non-Discrimination and Equality in the View of the UN Human Rights Treaty Bodies.” Human Rights Law Review 7 (1): 267–9, https://doi.org/10.1093/hrlr/ngl032.Suche in Google Scholar
Eidelson, Benjamin. 2015. Discrimination and Disrespect. Oxford, United Kingdom: Oxford University Press UK.10.1093/acprof:oso/9780198732877.001.0001Suche in Google Scholar
Epstein, Joshua M. 2012. Generative Social Science: Studies in Agent-Based Computational Modeling. Princeton: Princeton University Press.10.1515/9781400842872Suche in Google Scholar
Erev, Ido, and Ernan Haruvy. 2020. “Learning the Economics of Small Decisions.” In The Handbook of Experimental Economics, Vol. 2, edited by John H. Kagel, and Alvin E. Roth. Princeton: Princeton University Press.Suche in Google Scholar
Federal Anti-Discrimination Agency. 2010. Positive Maßnahmen zur Verhinderung oder zum Ausgleich bestehender Nachteile im Sinne des § 5 AGG. https://www.antidiskriminierungsstelle.de/SharedDocs/downloads/DE/publikationen/Expertisen/expertise_positive_massnahmen.pdf?__blob=publicationFile&v=3 (Accessed September 28, 2022).Suche in Google Scholar
Federal Anti-Discrimination Agency. 2019. Guide to the General Equal Treatment Act. https://www.antidiskriminierungsstelle.de/SharedDocs/downloads/DE/publikationen/Wegweiser/agg_wegweiser_engl_guide_to_the_general_equal_treatment_act.pdf?__blob=publicationFile&v=14 (Accessed September 26, 2022).Suche in Google Scholar
Federal Anti-Discrimination Agency. 2020. Bausteine f’́ur einen systematischen Diskriminierungsschutz an Hochschulen. https://www.antidiskriminierungsstelle.de/SharedDocs/downloads/DE/publikationen/Expertisen/bausteine_f_e_systematischen_diskrimschutz_an_hochschulen.pdf?__blob=publicationFile&v=5 (Accessed April 27, 2024).Suche in Google Scholar
Federal Anti-Discrimination Agency. 2021. Employer Obligations. https://www.antidiskriminierungsstelle.de/EN/about-discrimination/areas-of-life/work-life/obligations-of-employers/obligations-of-employers.html?nn=306544 (Accessed September 26, 2022).Suche in Google Scholar
Feldon, David F., James Peugh, Michelle A. Maher, Josipa Roksa, and Colby Tofel-Grehl. 2017. “Time-to-Credit Gender Inequities of First-Year PhD Students in the Biological Sciences.” CBE Life Sciences Education 16 (1), https://doi.org/10.1187/cbe.16-08-0237.Suche in Google Scholar
Fibbi, Rosita, Arnfinn H. Midtbøen, and Patrick Simon. 2021. Migration and Discrimination: IMISCOE Short Reader. Cham: Springer.10.1007/978-3-030-67281-2Suche in Google Scholar
Grim, Patrick, Daniel J. Singer, Christopher Reade, and Steven Fisher. 2015. “Germs, Genes, and Memes: Function and Fitness Dynamics on Information Networks.” Philosophy of Science 82 (2): 219–43. https://doi.org/10.1086/680486.Suche in Google Scholar
Haraway, Donna Jeanne. 1989. Primate Visions: Gender, Race, and Nature in the World of Modern Science. New York: Psychology Press.Suche in Google Scholar
Harding, Sandra. 1991. Whose Science? Whose Knowledge? Thinking from Women’s Lives. Ithaca: Cornell University Press.Suche in Google Scholar
Hellman, Deborah. 2016. “Two Concepts of Discrimination.” Virginia Law Review 102 (4): 895.Suche in Google Scholar
Holman, Bennett, and Justin P. Bruner. 2015. “The Problem of Intransigently Biased Agents.” Philosophy of Science 82 (5): 956–68. https://doi.org/10.1086/683344.Suche in Google Scholar
Icks, Annette, Bijedić Teita, Rosemarie Kay, Philipp Latzke, Andreas Merx, and Christian Mappala. 2022. Der Schutz vor Diskriminierung und die Förderung personaler Vielfalt im Arbeitsleben. https://www.antidiskriminierungsstelle.de/SharedDocs/downloads/DE/publikationen/Expertisen/Studie_Schutz_vor_Diskr_im_Arbeitsleben.pdf?__blob=publicationFile&v=3 (Accessed April 27, 2024).Suche in Google Scholar
Izquierdo, Luis R., Segismundo S. Izquierdo, and Fernando Vega-Redondo. 2012. “Learning and Evolutionary Game Theory.” In Encyclopedia of the Sciences of Learning, edited by Norbert M. Seel. Boston, MA: Springer.10.1007/978-1-4419-1428-6_576Suche in Google Scholar
Larivière, Vincent, Chaoqun Ni, Yves Gingras, Blaise Cronin, and Cassidy Sugimoto. 2013. “Bibliometrics: Global Gender Disparities in Science.” Nature 504 (7479): 211–3, https://doi.org/10.1038/504211a.Suche in Google Scholar
Lincoln, Anne E., Stephanie Pincus, Janet Bandows Koster, and Phoebe S. Leboy. 2012. “The Matilda Effect in Science: Awards and Prizes in the US, 1990s and 2000s.” Social Studies of Science 42 (2): 307–20. https://doi.org/10.1177/0306312711435830.Suche in Google Scholar
Longino, Helen E. 1990. Science as Social Knowledge: Values and Objectivity in Scientific Inquiry. Princeton: Princeton University Press.10.1515/9780691209753Suche in Google Scholar
Malueg, David. 2010. “Mixed-strategy Equilibria in the Nash Demand Game.” Economic Theory 44 (2): 243–70. https://doi.org/10.1007/s00199-009-0478-5.Suche in Google Scholar
Mayo-Wilson, Conor, Kevin Zollman, and David Danks. 2013. “Wisdom of the Crowds vs. Groupthink: Learning in Groups and in Isolation.” International Journal of Game Theory 42 (3): 695–723. https://doi.org/10.1007/s00182-012-0329-7.Suche in Google Scholar
Nash, John F. 1950. “The Bargaining Problem.” Econometrica 18 (2): 155–62. https://doi.org/10.2307/1907266.Suche in Google Scholar
O’Connor, Cailin, and Justin Bruner. 2019. “Dynamics and Diversity in Epistemic Communities.” Erkenntnis 84 (1): 101–19. https://doi.org/10.1007/s10670-017-9950-y.Suche in Google Scholar
Porat, Dina. 2005. Legislating Against Discrimination: An International Survey of Anti-discrimination Norms. Leiden: Martinus Nijhoff.10.1163/9789047415398Suche in Google Scholar
Rai, Arpana, and Upasna A. Agarwal. 2017. “Workplace Bullying Among Indian Managers: Prevalence, Sources and Bystanders’ Reactions.” International Journal of Indian Culture and Business Management 15 (1): 58–81. https://doi.org/10.1504/ijicbm.2017.10006293.Suche in Google Scholar
Rosenstock, Sarita, Cailin O’Connor, and Justin Bruner. 2017. “In Epistemic Networks, Is Less Really More?” Philosophy of Science 84 (2): 234–52. https://doi.org/10.1086/690717.Suche in Google Scholar
Rossiter, Margaret W. 1993. “The Matthew Matilda Effect in Science.” Social Studies of Science 23 (2): 325–41. https://doi.org/10.1177/030631293023002004.Suche in Google Scholar
Rubin, Hannah, and Cailin O’Connor. 2018. “Discrimination and Collaboration in Science.” Philosophy of Science 85 (3): 380–402. https://doi.org/10.1086/697744.Suche in Google Scholar
Schneider, Beth Z., William Carden, Alyson Francisco, and Thomas O. JonesJr. 2011. Women ‘Opting Out’of Academia: At what Cost. https://files.eric.ed.gov/fulltext/EJ944197.pdf (Accessed April 27, 2024).Suche in Google Scholar
Schneider, Mike, Hannah Rubin, and Cailin O’Connor. 2022. Promoting Diverse Collaborations, 54–72. Pittsburgh: University of Pittsburgh Press.10.2307/j.ctv31djr2f.7Suche in Google Scholar
Senatsverwaltung für Wissenschaft, Gesundheit, Pflege und Gleichstellung. 2022. Zum Verhältnis von Antidiskriminierung und Förderung. https://www.berlin.de/sen/frauen/recht/agg/verhaeltnis-agg-lgg/ (Accessed September 28, 2022).Suche in Google Scholar
Šešelja, Dunja. 2023. “Agent-Based Modeling in the Philosophy of Science.” In The Stanford Encyclopedia of Philosophy, edited by Edward N. Zalta, and Uri Nodelman, Winter 2023 ed.. Stanford: Metaphysics Research Lab, Stanford University.Suche in Google Scholar
Skyrms, Brian. 1994. “Sex and Justice.” Journal of Philosophy 91 (6): 305–20. https://doi.org/10.2307/2940983.Suche in Google Scholar
Skyrms, Brian. 2014. Evolution of the Social Contract, 2nd ed. Cambridge: Cambridge University Press.10.1017/CBO9781139924825Suche in Google Scholar
Skyrms, Brian, and Kevin J. S. Zollman. 2010. “Evolutionary Considerations in the Framing of Social Norms.” Politics, Philosophy and Economics 9 (3): 265–73. https://doi.org/10.1177/1470594x09339744.Suche in Google Scholar
Suff, Rachel. 2020. Managing Conflict in the Modern Workplace. https://www.cipd.org/globalassets/media/knowledge/knowledge-hub/reports/managing-conflict-in-the-workplace-2_tcm18-70655.pdf (Accessed April 25, 2024).Suche in Google Scholar
U.S. Equal Employment Opportunity Commission. n.d. Facts about Retaliation. https://www.eeoc.gov/facts-about-retaliation (Accessed April 29, 2024).Suche in Google Scholar
U.S. Equal Employment Opportunity Commission. 2021. Prohibited Employment Policies/Practices. https://www.eeoc.gov/prohibited-employment-policiespractices (Accessed September 30, 2022).Suche in Google Scholar
Ventura, Rafael. 2023. “Structural Inequality in Collaboration Networks.” Philosophy of Science 90 (2): 336–53. https://doi.org/10.1017/psa.2022.73.Suche in Google Scholar
West, Jevin D., Jennifer Jacquet, Molly M. King, Shelley J. Correll, and Carl T. Bergstrom. 2013. “The Role of Gender in Scholarly Authorship.” PLoS One 8 (7): 1–6. https://doi.org/10.1371/journal.pone.0066212.Suche in Google Scholar
Wippermann, Carsten. 2019. Sexismus im Alltag – Wahrnehmungen und Haltungen der deutschen Bevölkerung. https://www.bmfsfj.de/resource/blob/141246/b24dff04fcbf73ebf5e794a062e271ef/sexismus-im-alltag-pilotstudie-data.pdf (Accessed September 29, 2022).Suche in Google Scholar
Wladasch, Katrin, and Barbara Liegl. 2009. Positive Maßnahmen. Ein Handbuch zur praxistauglichen Umsetzung von Maßnahmen zur Bekämpfung von struktureller Diskriminierung und zur Herstellung von mehr Chancengleichheit. Wien: Ludwig Boltzmann Institut für Menschenrechte.Suche in Google Scholar
Young, H. P. 1993. “An Evolutionary Model of Bargaining.” Journal of Economic Theory 59 (1): 145–68. https://doi.org/10.1006/jeth.1993.1009.Suche in Google Scholar
Zhang, Sarah, James F. M. Cornwell, and E. Tory Higgins. 2014. “Repeating the Past: Prevention Focus Motivates Repetition, Even for Unethical Decisions.” Psychological Science 25 (1): 179–87. https://doi.org/10.1177/0956797613502363.Suche in Google Scholar
Zheng, Lily. 2020. “Do Your Employees Feel Safe Reporting Abuse and Discrimination?” https://hbr.org/2020/10/do-your-employees-feel-safe-reporting-abuse-and-discrimination (Accessed April 29, 2024).Suche in Google Scholar
Zollman, Kevin J. S. 2007. “The Communication Structure of Epistemic Communities.” Philosophy of Science 74 (5): 574–87. https://doi.org/10.1086/525605.Suche in Google Scholar
Zollman, Kevin J. S. 2010. “The Epistemic Benefit of Transient Diversity.” Erkenntnis 72 (1): 17–35. https://doi.org/10.1007/s10670-009-9194-6.Suche in Google Scholar
Supplementary Material
This article contains supplementary material (https://doi.org/10.1515/krt-2024-0014).
© 2024 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.

