Numerical and experimental study of the dynamic factor of the dynamic load on the urban railway

1 Introduction

Dynamic load is an important value in the railway design process. Thus, accurate study of the DLF will lead to safe and economical designs. However, determining the DLF is a rather complicated problem because of the interaction between rail and moving vehicles.

The dynamic load is generally expressed as a function of the static load (Eq. 1) [1]

Where P_d is the dynamic wheel load, ∅ is the dynamic wheel load factor (∅ > 1), and P_s is the static wheel load.

Studies by authors around the world have published research results on dynamic load of railway. In 1953, Talbot [2] had given a dynamic load factor that relates to train speed and wheel diameter for heavy haul railway with the train speed less than 80 km/h. In 1969, Indian Railways had proposed dynamic load factor for narrow gauge track incorporates track modulus and train speed [3]. Eisenmann (1972) had used dynamic load factor for high speed railway track that incorporates train speed and the condition of the track [4]. The Office of Research and Experiments (ORE) of the International Union of Railways and Birmann [5] had proposed dynamic load factor for speeds up to 200 km/h incorporates the track geometry, vehicle suspension, vehicle speed, vehicle center of gravity, age of track, curve radius, super-elevation, and cant deficiency. The Germany Railways (1943) using an equation with the train speed is no more than 200 km/h to calculate the dynamic load factor only using train speed [6]. The dynamic load factor formula is used for South African Railways is similar to the Talbot formula, but is calculated for narrow gauge track [2]. Clarke formula algebraically combines the Talbot and Indian Railways dynamic load factors [7]. In 1968, a dynamic load factor only depended on the train speed was prepared for the Washington Metropolitan Area Transit Authority (WMATA) and used in subsequently recommended standards for transit trackwork [8]. In 2010, Sadeghi had proposed a dynamic load factor in Iran. This factor depends on train speed [9]. The speed of the train is no more 200km/h. The use of the AREMA recommendation for dynamic impact factor is suggested for the railway with the train speed from 32 km/ h to 193 km/ h [10]. The China Railways proposed dynamic load factors that depend on train speed and wheel load shift coefficient in curves. This factor is used for high speed railway [11]. In 2017, Leonid and Andrey had researched dynamic live load factor for bridge structures on High speed railway [12].

In this study, the authors studied the DLF for the urban railway based on field measurement and simulation calculations. The strain gage is used to measure relative deformation. Simulation calculations are implemented by SIMPACK software.

2 Experimental method to determinate DLF

2.1 Test equipments

The rail is mounted the equipment to measure deformation. Relative deformation was measured by the strain gage with length 10mm. Strain gage was placed at the bottom center of the rail foot (Figure 1).

Figure 1

The strain gage

2.2 Load test arrangements

Test loads are trains on Cat Linh – Ha Dong urban railway line as Figure 2.

Figure 2

The train of Cat Linh – Ha Dong urban railway line

Each train includes 4 cars [13] with the following set-up method: + Tc-M + M-Tc such as Figure 3, in which:

Figure 3

Model of the train

“+”: semi-automatic central buffer coupler

“−”: Semi-permanent central buffer coupler

“M”: motor car

“Tc”: trailer car

Load arrangement of the train is set up such as Figure 4

Figure 4

Model of test train load

2.3 Test results

Figure 5 shows the dynamic deformation time-history curves of the rail foot in the first test point on Cat Linh – Ha Dong urban railway line with train speed V = 30 km/h. The maximum of dynamic deformation is 0.00011732.

Figure 5

Dynamic deformation versus time for train speed V = 30km/h

Figure 6 shows the dynamic deformation time-history curves of the rail foot in the second test point on Cat Linh – Ha Dong urban railway line with train speed V = 50 km/h. The maximum of dynamic deformation is 0.000127.

Figure 6

Dynamic deformation versus time for train speed V = 50km/h

Figure 7 shows the dynamic deformation time-history curves of the rail foot in the third test point on Cat Linh – Ha Dong urban railway line with train speed V = 80 km/h. The maximum of dynamic deformation is 0.000145.

Figure 7

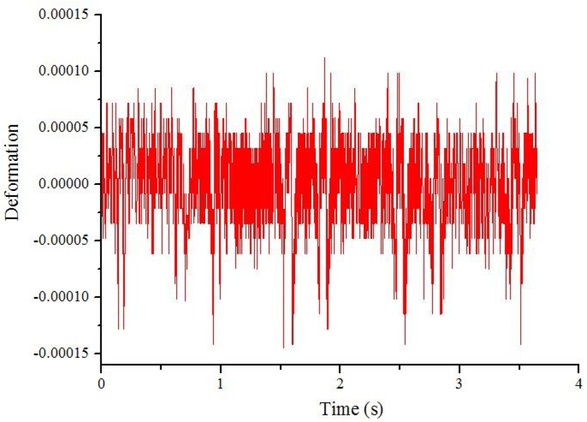
Dynamic deformation versus time for train speed V = 80km/h

Measuring the static deformation of the rail we have the following results:

Table 1

Table of results of static deformation

No.	Measurement times	Static deformation
1	The first	0.00010735
2	The second	0.00010519
3	The third	0.00010004
	Average value	0.00010419

Some typical results of the dynamic load factors are depicted in the form of graphs comprising load histories under different train speeds (Figure 8).

Figure 8

Dynamic load factors increasing due to speed for urban railway

By using linear regression analysis of the DLF. Using Minitab simulation software. The results from the minitab software are as follows

Regression equation

Φ=0.9909+0.004853.V

Coefficients

Term	Coef	SE Coef	T-Value	P-Value	VIF
Constant	0.9909	0.0124	79.94	0.000
V	0.004853	0.000250	19.38	0.003	1.00

Model Summary

S	R-sq	R-sq(adj)	R-sq(pred)
0.0146026	99.47%	99.21%	96.25%

Analysis of variance

Source	DF	Adj SS	Adj MS	F-Value	P-Value
Regression	1	0.080074	0.080074	375.52	0.003
V	1	0.080074	0.080074	375.52	0.003
Error	2	0.000426	0.000213
Total	3	0.080500

The equation of DLF is proposed such as Eq. 2.

(2)Φ=0.9909+0.004853.V

Where V is velocity (km/h)

It can be seen that the values of dynamic load factor increasing due to speed such as Eq. 2. It was created based on support stiffness, rail material, train load and train speed.

3 Application of software to simulate dynamic model vehicle-track interactions

3.1 Numerical simulation process

The model of vehicles is included 3 parts: car body, bogie and wheel set. Each part of the system has five degrees of freedom: bouncing, lateral, rolling, yawing and pitching. So, each car has 35 degrees of freedom as follows in Table 2.

The model of track structure with the continuous elastic point support model uses a series of point support spacing intervals of the discrete elastic (Figure 9, 10).

Figure 9

Track structure lateral view

Figure 10

Track structure side view

These models are established using SIMPACK software to simulate the model of urban railway dynamic such as Figure 11 to 14.

Figure 11

Simulation of wheel model of Cat Linh – Ha Dong line

Table 2

Vehicle vibration model degrees of freedom

Freedom	Bouncing	Lateral	Rolling	Yawing	Pitching
Car body	Zc	Yc	ϕc	ψc	βc
Front bogie	Zt1	Yt1	ϕt1	ψt1	βt1
Rear bogie	Zt2	Yt2	ϕt2	ψt2	βt2
First wheel set	Zw1	Yw1	ϕw1	ψw1	βw1
Second wheel set	Zw2	Yw2	ϕw2	ψw2	βw2
Third wheel set	Zw3	Yw3	ϕw3	ψw3	βw3
Fourth wheel set	Zw4	Yw4	ϕw4	ψw4	βw4

Table 3

The specifications of the urban railway train

No.	Technical parameters	Symbols, units	Values
1	Mass of car body	Mc [ton]	22.4
2	Mass of frame	Mt [ton]	3.52
3	Mass of wheel set	Mw [ton]	1.539
4	The car body around the X axes’ rotational inertia;	Icx [ton.m2]	23.2
5	The car body around the Y axes’ rotational inertia;	Icy [ton.m2]	943
6	The car body around the Z axes’ rotational inertia;	Icz [ton.m2]	941
7	The bogie around the X axes’ rotational inertia;	Itx [ton.m2]	1.43
8	The bogie around the Y axes’ rotational inertia;	Ity [ton.m2]	1.76
9	The bogie around the Z axes’ rotational inertia;	Itz [ton.m2]	2.96
10	The wheel set around the X axes’ rotational inertia	Iwx [ton.m2]	0.801
11	The wheel set around the Y axes’ rotational inertia	Iwy [ton.m2]	0.104
12	The wheel set around the Z axes’ rotational inertia	Iwz [ton.m2]	0.814
13	The distance between two bogie centre plates	2L [mm]	12,600
14	The distance between two wheel axes	Lt [mm]	2,200
15	The hight from the rail surface to the center of the body	Hc [mm]	1,800
16	The height from the rail surface to the center of the bogie	Hf [mm]	500
17	The lateral distance between two axle box springs	2dw [mm]	1,930
18	The lateral distance between two air springs	2ds [mm]	1,850
19	The longitudinal distance between two axle box springs	2c1 [mm]	550
20	The height from the top of the air spring to the center of the body	hc [mm]	1,005
21	The height from the bottom of the air spring to the center of the bogie	hf [mm]	196.8
22	Height from rail surface to damper	H2 [mm]	697
23	The height from the rail face to the restraining bar	H3 [mm]	465
24	Diameter of wheel	D [mm]	840
25	Distance between two wheel rollers	2S [mm]	1,493
26	Longitudinal stiffness of one side of the air spring	Ksx [MN/m]	0.21
27	Lateral stiffness of one side of the air spring	Ksy [MN/m]	0.21
28	The vertical stiffness of one side of the air spring	Ksz [MN/m]	0.45
29	Longitudinal stiffness of an axle box	Kpx [MN/m]	10.6
30	Lateral stiffness of an axle box	Kpy [MN/m]	7.8
31	Vertical stiffness of an axle box	Kpz [MN/m]	1.7
32	Lateral damping coefficient of air springs	Csy [kN.s/m]	30.0
33	Vertical damping coefficient of air springs	Csz [kN.s/m]	60.0
34	Vertical damping coefficient of axle box springs	Cpz [kN.s/m]	10.0

Figure 12

Simulation of bogie model of Cat Linh – Ha Dong line

Figure 13

Simulation of car body model of Cat Linh – Ha Dong line

3.2 Results

The dynamic load of the wheels acting on the rails when the cars of Cat Linh – Ha Dong line run on the rails with train speed V = 30 km/h are shown in Figure 15. The maximum of dynamic load is 48.625 kN.

Figure 14

3D model calculating dynamic of car of Cat Linh – Ha Dong line

Figure 15

Graph of vertical dynamic force of wheel load acting on rail with V = 30 km/h

The dynamic load of the wheels acting on the rails when the cars of Cat Linh – Ha Dong line run on the rails with train speed V = 50 km/h are shown in Figure 16. The maximum of dynamic load is 52.883 kN.

Figure 16

Graph of vertical dynamic force of wheel load acting on rail with V = 50 km/h

The dynamic load of the wheels acting on the rails when the cars of Cat Linh – Ha Dong line run on the rails with train speed V = 80 km/h are shown in Figure 17. The maximum of dynamic load is 59.228 kN.

Figure 17

Graph of vertical dynamic force of wheel load acting on rail with V = 80 km/h

It can be seen that the experimental results of dynamic load factors are similar to the simulation values. These results are compared with the results of other authors that are suitable [7].

Table 4

Comparison of dynamic load factor

Velocity	Dynamic load factor		Deviation
	Experiment results	Simulation results	ration
30 km/h	1.13	1.15	1.77%
50 km/h	1.22	1.25	2.46%
80 km/h	1.39	1.40	0.72%

Figure 18

Comparison of dynamic load factor with other authors

4 Conclusions

The authors performed DLF research and proposed a DLF function for the urban railway in Vietnam. The results can be used to provide design flexibility and broadening the design principle. Besides, this study may also support in calculating railway maintenance and repair. There are many dynamic load factors for railway, but in this article, the authors assess DLF on the urban railway in Vietnam (1,435 mm gauge). In the future, the next development direction is to study DLF for prestressed concrete sleepers of narrow railway (1,000mmgauge) and high speed railway (1435mm gauge) in Vietnam.