Scaling Oversmoothing Factors for Kernel Estimation of Spatial Relative Risk

2.1 Estimator

Falling within some geographical region , we observe two spatial point patterns and which represent cases and controls, respectively. Assuming that X and Y have arisen from independent Poisson processes with respective densities f and g, the goal in practice is to estimate the ratio in order to attain the relative risk surface (Bithell 1990, 1991). The initial work by Kelsall and Diggle (1995) explored in detail the substitution of these unknown densities with corresponding planar kernel density estimates and , giving

[1]

where

[2]

and where for some kernel function K, and is an edge-correction factor.

Controlling the amount of smoothing applied to the observations via the kernel function, and are critical to the quality of the estimates from eq. [2]. A poor (i.e. too large or too small) choice of bandwidth for a given estimate has the result of providing an unrealistic impression of the true density. Preference is therefore typically given to some form of “data-driven” bandwidth selection, as opposed to subjective selection, which is often simply based on a visual inspection of the estimate.

Of lesser importance when compared with “appropriate” selection of the bandwidth(s) is the choice of K (see e.g. Wand and Jones 1995; Silverman 1986). For theoretical convenience, it is usually preferable to choose K as a radially symmetric probability density – and the Gaussian kernel (where represents Euclidian norm) is arguably the most common kernel used in the applied literature. Given the practical focus of this work, we will therefore implement the Gaussian K in the subsequent investigations.

Finally, note that it is often sensible to work with the estimated risk function [1] on the log-scale, giving . Kelsall and Diggle (1995) argue that this is important, as in performing this transformation we are effectively “[treating] the two sets of points symmetrically”. We will proceed based on this recommendation.

2.2 Asymptotic properties

In their asymptotic investigation into the properties of the kernel density-ratio estimator in which they make some standard regularity assumptions, Kelsall and Diggle (1995) are able to show that

[3]

and

[4]

for points z which lie inside a reasonable distance away from the edge (this is primarily determined by the magnitude of the smoothing parameters). In eq. [3], we have that and . In eq. [4], .

With these properties, we note that a “bias/variance trade-off” exists, a feature typical of smoothing problems. Larger bandwidths will increase bias at a reduction in variability and smaller bandwidths will have the opposite effect. In terms of the bias, however, eq. [3] suggests that we can effectively eliminate much of the bias for the log-risk function in areas where if we choose a common case–control bandwidth . Based on this, and some numerical results, Kelsall and Diggle (1995) concluded that choosing h to be the same for both and was preferable to choosing and separately. This finding in turn motivated Davies and Hazelton (2010) to briefly experiment with Terrell’s oversmoothing principle for choosing a common h (based on pooling the case–control data) in estimation of the risk function, due to the corresponding reduction in variance. The hope was that the potential bias cancelations where the two densities are very similar would prevent excessive overall bias, which has been noted as a potential concern when using the oversmoothing factor in standalone density estimation (Terrell, 1990; Wand and Jones, 1995). It turned out that the oversmoothing bandwidth appeared to perform quite well where it was used in that work, which motivates the current article where attention is focused on further investigation and fine tuning of this potentially beneficial and computationally inexpensive approach to risk function bandwidth calculation.

3.1 Factor

In his seminal work, George Terrell introduced the idea of the maximal smoothing principle in the context of density estimation via the histogram and the kernel estimator (Terrell 1990). The author demonstrated that knowledge of the scale of the recorded data “gives us tight upper bounds on the asymptotically optimal histogram bin width or kernel [bandwidth]”. It is then possible to use these properties to find such a smoothing parameter which satisfies this criterion, providing the oversmoothing bandwidth. As Terrell (1990) points out, this bandwidth, which is described as “the most smoothing compatible with the scale of the problem”, is taken to produce “conservative” density estimates which “tend to eliminate accidental features”. This is appealing from the point of view of kernel estimation of the relative risk function – although we may quite rightly be concerned about bias as a result of using a large bandwidth, the fact that we already are aware of the potential bias cancelations visible in eq. [3] for areas with means the corresponding reduction in variability in eq. [4] is particularly attractive from a practical perspective.

Defined generally for data of dimension d, Terrell (1990) provides the expression

where is the covariance matrix estimated from the observed data, and denotes the Gamma function. This provides the bandwidth matrix, which specifies different degrees of smoothing along each of the d axes (this type of structure is discussed a little more momentarily). Terrell (1990) also remarks that there exist other spread statistics which may be used in place of .

For our purposes, we are interested in isotropic smoothing on ; this is by far the most common dimension and smoothing style encountered in real-world applications of the kernel log-relative risk function (indeed, this author is currently unaware of any deviations from this scheme in the applied literature). Let the desired scalar bandwidth be denoted , which is found with

where U is a scalar term giving a single measure of spread (on the scale of standard deviation) for the data set at hand. The factor OS is found by simplification of the square-bracketed term above when and is given with

[5]

Note that for a Gaussian K, it is easy to show that .

Thus, the objective here is to find a scaling parameter U, such that we do not inappropriately mask or amplify [5]. To do this for our case–control data, we first pool the two data sets such that . Crucially, this in a way means we assume that the case and control distributions share a similar spatial behavior. Where we cannot make this assumption, it may be more sensible to access the few methods designed for density-ratio bandwidth selection which retain the distinction between case and control marks. However, current work in Davies (2013) highlights the myriad of practical problems associated with these more complicated methods. As such, it should be stressed that use of OS in this setting is a computationally and conceptually simpler alternative to methods designed specifically for case–control data, but one with an equally important role to play should fast and stable bandwidth selection for exploratory data analysis via the kernel-smoothed risk function be key.

Continuing along this thread, pooling the two samples would typically imply that in eq. [5]. Often in practice, however, there is a notable difference in sample sizes (most commonly there are more controls than cases). In the same way, we must take care in choosing U such that it is representative of the “overall” scale of the data, we must also be wary of calculating OS. If indeed , we do not wish this bandwidth factor to be “blurred” (i.e. too heavily influenced) by an large total sample size if there is such a distinct discrepancy between the counts in the two groups. In an effort to assist sensitivity to a possible large difference between and , we replace n in eq. [5] by .

The “geometric mean sample size” , which results in a value that falls between the two sample sizes yet closer to the smaller, is based primarily on the above heuristic reasoning. The presence of very different case–control sample sizes is not at all uncommon in practice and the need to be wary of potential adverse effects resulting from pooling the data sets should be kept in mind. We therefore assume that this is implemented in studying the relative risk surface estimates below. Our perceptions of the relative performances of the various scaling methods studied in the simulations in Section 4 are not affected by such a decision. Rather, it is the implementation of for individual data sets in practice where becomes more important.

It is also worth once more highlighting that our use of OS in this context, and indeed our investigation of various scalar U in the following sections, clearly implies imposition of isotropic smoothing. This raises the question as to how appropriate this approach will be in situations where the x- and y-coordinates of a given point pattern are on very different scales. In such a setting, we may need to turn to implementation of more complicated bandwidth matrices , which can allow for different levels of smoothing along each axis. Another option is to re-scale the raw data so that these differences in axis scalings are eliminated – a process referred to as sphering. The density/risk surface may then be isotropically smoothed, and the result back-transformed to the original scales. That being said, there is no theoretical evidence to suggest that this is appropriate for anything but Gaussian-distributed data (cf. Chapter 4 of Wand and Jones 1995). At any rate, the computational simplicity and ease-of-use of remains practically appealing, particularly for quick exploratory purposes. As mentioned briefly above, in this author’s experience with applications of the kernel-smoothed relative risk function to real-world epidemiological data to date, there have been no compelling reasons to employ anisotropic smoothing.

Davies and Hazelton (2010) used a straightforward estimate of U by computing the mean of the Gaussian-scaled interquartile ranges (IQR) of the coordinates in Z on both x- and y-axes (see also Silverman 1986). This represents a so-called axis-specific measure of spread and is an admittedly simple fix to the problem of finding a scalar U for the bivariate data sets. In the simulations which follow, we will therefore also compare the triangle-based methods with an appropriate axis-specific counterpart (see the definition for XY.MAD below).

3.2 Trigonometric methods

The approaches described here were inspired by the interesting work in Rousseeuw and Hubert (1996), where the aim is to estimate the error variance in simple linear regression without the need to turn to residuals of the fitted line itself. A subsequent evaluation of Rousseeuw and Hubert’s technique was shown to perform its role well in Schettlinger et al. (2010). We build on these ideas to make them relevant to choosing a suitable U based on spatial point process data and estimation of the risk function.

Consider the network of up to non-degenerate triangles formed by the spatial observations on as per Figure 1 (instances of three distinct collinear points are ignored). Scale may then be estimated from suitable interior measurements involving these triangles. We consider two different versions of trigonometric scaling here. First, the grand mean interior triangle height and width, and second, the grand mean of a certain proportion of the medians of the triangles.

Figure 1

The network of 120 triangles formed by 10 randomly generated points

The first scaler we explore is computed as the grand mean interior widths and heights of the triangles. Use of these width and height measurements represents a straightforward modification of the technique in Rousseeuw and Hubert (1996), who appropriately used height measurements only in their regression variance problem. The fact that this appeared to perform well in that setting provides some heuristic reasoning to experiment with our width–height scaler here. Given any non-degenerate triangle ABC with a positive area, the interior width and height values can easily be computed by sorting the x- and y-axis values and some elementary geometry. First, assume the vertices , , and are sorted according to the x-coordinate, i.e. we will have either or such that . Then the vertical height measurement associated with this triangle, , is given as

where denotes absolute value. For the horizontal width of a non-zero area triangle, , we now assume the vertices A, B, and C are labeled with respect to increasing y-coordinate values, in the sense that we will now have either or with . Then,

For convenience, the left column of Figure 2 provides illustrative examples showing the widths and heights of three different triangles. As we can see, these measurements will always parallel the two axes. With a total of N triangles formed by the points in Z, the corresponding triangle-based width–height scaler (TRI.WH) for OS is given with

[6]

Figure 2

Three different illustrative examples of the width–height lengths (left column) and the medians (right column) obtained from possible triangles. In the triangle median plots, the represents the centroid, with the bold-dashed portion of each median representing the “two-thirds” used in the MAD calculation

where the subscript i refers to the ith distinct triangle with vertices ABC.

The second scaler is motivated by the three medians, , , and , of each non-degenerate triangle. Triangle medians, which protrude internally from each vertex to the midpoint of the opposite side, all meet at the same point – the centroid. The distance along each median from the vertex which spawns it to the centroid is always twice as long as the remaining distance from the centroid to the opposite edge. Use of Apollonius’ theorem yields the total median lengths:

A triangle centroid, whose coordinates are computed as the mean of A, B, and C, is interpreted as the “center of balance” of an “evenly weighted” set of vertices. As such, knowledge of the median lengths affords us a convenient approach to estimation of a scalar measure of spread for point process data, analogous to the mean absolute deviation (MAD) in the univariate setting. Inspection of the right-hand column of Figure 2 shows why this is the case: by making use of two-thirds of each median length and averaging, we are effectively computing the scalar MAD for our 2-dimensional data. In the same fashion as the TRI.WH scaler, the TRI.MAD scaler for OS will be computed by taking the grand mean of all “two-third” median lengths, namely

[7]

where denotes the median from vertex A of the ith distinct triangle ABCi; similarly for and .

The TRI.MAD scaler is particularly appealing in that the triangle medians are not restricted in terms of angular movement. Intuitively, by using TRI.MAD, we therefore might hope to capture “more information” from our planar-dispersed data in computation of the required scaling parameter when compared with a measure such as TRI.WH (or indeed an even simpler axis-specific value for U). To help demonstrate this, we also use in the following section the axis-specific version of the mean absolute deviation scaler XY.MAD, which is simply the mean of the univariate MAD of all x-axis and y-axis coordinates computed separately, for all n points in the pooled case–control data set Z. More formally, let and denote all x- and corresponding y-coordinates in Z respectively. Then,

[8]

where

with and .

4.1 Scenario definitions

We compare the performance of the various scaling approaches to OS in five synthetic problem scenarios, all defined on the unit square such that . For each scenario, the “true” control density g is defined in terms of normal mixtures, and scaled to integrate to unity over . A corresponding “true” relative risk surface r is then defined using a particular formulation involving exponential functions. Additional scaling takes place for r to ensure. At each iteration, controls are sampled randomly from g. Case “candidates” are sampled from g and accepted/rejected with probabilities proportional to r, until the desired number is reached. Figure 3 displays filled contour plots of the control densities, case densities, and corresponding risk functions for the five problems; the specific formulations are provided in Table 1. In this table, represents the bivariate Gaussian density edge corrected to , centered at a and standard deviation b ( refers to the identity matrix). All computations are performed using the statistical programming environment R (R Development Core Team, 2012), using the contributed packages spatstat (Baddeley and Turner 2005) for random point generation, and sparr (Davies et al. 2011) for risk function estimation.

The scenarios have been designed in an effort to loosely reflect what we may be likely to observe in practice. In Problem 1, we observe a mildly bimodal yet quite “gentle” dispersion of raw risk ranging from 0.82 to 1.73. There are three distinct modes in both the control and risk functions of Problem 2; the risk reaches higher levels over an interval of . Problem 3 has an underlying control population characterized by an elongated “bump” and a smaller circular density on the western border. There exists a small, sharp peak in risk within the latter area, with the raw risk ranging from 0.39 to 3.34. Problem 4 exhibits several areas of point aggregation surrounding a larger central mode and a corresponding risk interval of . The final problem, Problem 5, is designed in contrast to the others to have an extreme maximum risk value. The control density is perfectly uniform, but the risk surface now includes a tight peak in the center of ; risk interval is . Though less likely to occur in practice, this scenario will be an interesting comparison to the others. Some additional comments concerning computational costs of the trigonometric methods are warranted. In practice, evaluation of the total network of triangles for a given pattern of size n would require operations. This quickly increases the computational expense beyond tolerable levels for sample sizes much larger than, say, . This problem can be avoided by taking the required measurements on a suitably large random sample of the possible triangles; the number of triangles used subsequently replaces N in eqs [6] and [7]. In the simulations which follow, we will compute these scalers based on 20,000 randomly sampled triangles, which keeps computational expense relatively small. Some experimentation (not shown here) revealed increasing this number did little to change the estimated scaling factor in each case.

Figure 3

Filled contour plots of the pre-determined control densities (left column), evaluated case densities (middle column), and pre-determined log-risk functions (right column) for the five problem scenarios. Note that the case density formulae are not explicitly given as these functions are simply evaluated as the product of the control density and the (raw) risk function following the design. To highlight this, the f header is parenthesized

Table 1

Definitions of control densities g and risk functions r for the synthetic problem scenarios

Problem	Target definition
1
2
3
4
5

4.2 Discrepancy results

To provide some comparative measure to the OS bandwidths using TRI.WH, TRI.MAD, and the simpler XY.MAD, we run the simulations including risk functions estimated using bandwidths calculated by the common single-density least-squares cross-validation (LSCV) on the pooled data Z. This is of particular interest as LSCV bandwidths are chosen to approximately minimize the mean ISE with the true density. A good general discussion on LSCV can be found in e.g. Bowman and Azzalini (1997).

The performance of the different scaling measures for OS (TRI.WH, TRI.MAD, and XY.MAD), as well as use of the LSCV bandwidths, is measured in terms of the ISE of the iterated log-risk surfaces with the true . That is, ISE . We also use a weighted ISE, WISE , which aims to amplify the error in areas where there exist risk peaks or “hotspots” (typically of interest in practice).

Simulations are carried out over 200 iterations for two sample size sets: and . As mentioned above, use of the trigonometric scaling approaches was restricted at each iteration to a random sample of 20,000 non-degenerate triangles and it was found that increasing this to much larger values did little to improve performance at a noticeable increase in computational expense. Boxplots of the ISE and WISE for the simulations are displayed in Figures 4 (Problems 1 to 3) and 5 (Problems 4 and 5), and Table 2 provides means and standard deviations of these error measures in each situation.

Figure 4

Boxplots of the log(ISE) (left) and log(WISE) (right) with (white) and (gray) for Problems 1–3

Figure 5

Boxplots of the log(ISE) (left) and log(WISE) (right) with (white) and (gray) for Problems 4 and 5

Table 2

Means and parenthesized standard deviations of the ISE and WISE results obtained in each setting

Problem	Method	ISE		WISE
1	TRI.WH	8.48 (0.84)	7.13 (0.82)	5.23 (0.83)	3.88 (0.82)
	TRI.MAD	8.19 (0.82)	6.88 (0.80)	4.94 (0.82)	3.64 (0.80)
	XY.MAD	9.17 (0.85)	7.73 (0.85)	5.92 (0.85)	4.48 (0.85)
	LSCV	10.45 (0.92)	9.52 (0.91)	7.20 (0.93)	6.27 (0.92)
2	TRI.WH	5.85 (0.42)	4.92 (0.32)	3.74 (0.54)	2.90 (0.43)
	TRI.MAD	5.81 (0.42)	4.90 (0.31)	3.71 (0.54)	2.88 (0.42)
	XY.MAD	6.27 (0.43)	5.26 (0.34)	4.16 (0.57)	3.24 (0.50)
	LSCV	6.98 (0.80)	6.21 (0.49)	4.93 (0.95)	4.27 (0.70)
3	TRI.WH	10.56 (0.91)	9.04 (0.91)	10.43 (0.92)	8.91 (0.92)
	TRI.MAD	9.56 (0.91)	8.09 (0.86)	9.42 (0.93)	7.94 (0.88)
	XY.MAD	10.65 (0.88)	9.16 (0.90)	10.52 (0.89)	9.03 (0.91)
	LSCV	11.64 (0.74)	11.39 (0.67)	11.52 (0.74)	11.26 (0.67)
4	TRI.WH	5.94 (0.46)	5.00 (0.34)	2.89 (0.56)	2.67 (0.33)
	TRI.MAD	5.92 (0.46)	4.98 (0.34)	2.90 (0.56)	2.67 (0.33)
	XY.MAD	6.44 (0.46)	5.44 (0.37)	2.84 (0.61)	2.52 (0.38)
	LSCV	7.34 (0.86)	6.90 (0.55)	3.08 (0.54)	2.40 (0.45)
5	TRI.WH	5.68 (0.34)	4.89 (0.21)	5.25 (0.28)	4.97 (0.18)
	TRI.MAD	5.69 (0.34)	4.89 (0.21)	5.25 (0.28)	4.96 (0.19)
	XY.MAD	6.03 (0.34)	5.07 (0.23)	5.09 (0.38)	4.73 (0.25)
	LSCV	5.60 (0.66)	4.92 (0.38)	5.26 (0.41)	4.98 (0.48)

Inspection of the ISE results for Problem 1, we note the TRI.MAD OS bandwidths provide some level of improvement in both median ISE and WISE over the other considered options. TRI.WH also performs well, with the axis-specific scaling measure, XY.MAD, struggling somewhat to match the overall performance of the other two scalers for OS. Use of the LSCV bandwidth is the worst performer in this setting; the relatively mild risk increase over a sizeable portion of for this problem has called for larger bandwidths naturally provided by the OS factor.

The differences in errors between the TRI.WH and TRI.MAD OS scalers for Problem 2 are almost indistinguishable. The LSCV methodology has again fallen behind OS in terms of median ISE and WISE, the relative instability in this bandwidth selection mechanism is also apparent with a larger spread of errors. Problem 3 exhibits both a wide risk “bump” and a tall sharp spike. Results indicate the OS bandwidth with TRI.MAD scaling has clearly provided the best median measures of ISE. TRI.WH scaling retains a second-place position, albeit with very similar behavior to axis-specific XY.MAD scaling. Once more, the LSCV bandwidths are inferior. Even with the WISE increasing the error “importance” where the tight risk hotspot is at its highest, oversmoothing with TRI.MAD remains the favorable option.

Problem 4, with many small risk hotspots, and Problem 5, with the single excessive risk spike, continue to support TRI.MAD and TRI.WH as the best scalers (followed closely by XY.MAD) in terms of median ISE (similar to the results for Problem 2). However, things begin to change when we examine the WISE results for these two problems. As the risk fluctuations have become much larger (recall the maximums of 3.91 and 9.45 for 4 and 5, respectively), the weighting has finally begun to move the errors in favor of the smaller bandwidths which tend to be provided by LSCV. This is understandable, as there would naturally exist a point at which oversmoothing will be unable to adequately capture the true risk magnitudes as they become extreme. Despite this, WISE is entirely dependent upon the scale of the weighting, and it could sensibly be argued that such risk levels (particularly as in Problem 5) are less likely to be observed in practice.

A broad interpretation of these results indicate that the TRI.MAD and TRI.WH scalings, coupled with OS, provide good risk function estimates in terms of overall error, especially when we do not expect excessive peaks in the risk surface (which is typically the case in this author’s experience). Use of the simpler alternative that is XY.MAD scaling can also perform well under certain conditions, but not as consistently as TRI.MAD. Implementation of LSCV for such problems appears somewhat less appealing in light of these findings.

4.3 Empirical sampling distributions under CSR

The question of just how the various triangle measurements are distributed based on a given point pattern is a difficult question to answer. Such knowledge would be useful in understanding more about the role of such methods for provision of a univariate measure of scale for our bivariate data. In order to shed some initial light on this issue, a sensible starting point is to consider the empirical sampling distributions of these quantities under the assumption of complete spatial randomness (CSR).

As a quick experiment, point patterns of size 200 and 1,400 are generated in the unit square under CSR. In each of 200 iterations for each sample size, 20,000 triangles are again randomly selected, and the widths, heights, and medians are computed. Note that given the square window and the fact that the width–height measurements will always parallel the two axes, the distribution of triangle widths under CSR will be identical to that of the heights. Histograms corresponding to the total collection of widths and medians for the larger sample size are plotted in Figure 6.

Figure 6

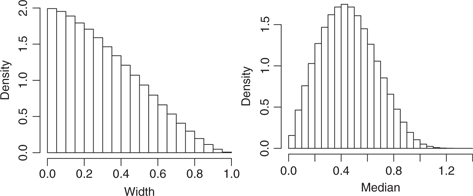
Histograms of the recorded triangle widths (left) and medians (right) for point patterns generated under the condition of complete spatial randomness

We note a steadily decreasing sampling distribution for the triangle widths, bounded by zero and the maximum width of the study window, 1. By comparison, the distribution of medians is unimodal with a slight right skew. A cursory examination of the corresponding collections of widths and medians from data sets arising from the synthetic problem scenarios in Section 4 (not shown) reveals these distributions in all cases to closely resemble those in Figure 6. This is not necessarily surprising – we must keep in mind that with these triangle measurements we are merely attempting to provide a univariate measure of scale for these point patterns. Thus, since the study window has not changed, and all generated point patterns under these scenarios yield some form of point coverage over much of the unit square (even if some areas tend to be “heavier” in point concentration than others), we should expect the overall distributions of triangle measurements to remain very similar to one another. Where we can expect this to change is the situation in which points only occupy a relatively small portion of the window, with few if any observations anywhere else. A deeper investigation into these sampling distributions and their behavior, both theoretically and practically, would make an interesting future research problem.