On the Use of Quantity Calculus
-
Tomislav Cvitas
Quantity calculus is a system of algebra in which symbols are consistently used to represent physical quantities and not their numerical values expressed in certain units. We always take the values of physical quantities to be the products of a numerical value and a unit, and we manipulate the symbols for physical quantities, numerical values, and units by the ordinary rules of algebra. A more appropriate name for “quantity calculus“ might be “algebra of quantities”, because the principles of algebra rather than calculus are involved.
Each symbol of a physical quantity (single letter, italic) in an equation stands for the value of the quantity which is
(quantity) = (numerical value) × (unit) (1)
In this way the equations hold for any unit as we believe the laws of nature should. Units are a matter of human choice, and no law in nature should depend on them. For example,
force = mass × acceleration
or, with symbols,
F = m a (2)
irrespective of what units we choose. Equations should therefore be written in a form not implying certain units. In applications with many repetitive calculations, it is often convenient to write equations with numerical values in certain units. Then, however, different symbols should be used. Equation (2) can for a certain purpose be written in the form
{F}N = {m}kg • {a}m s–2
or
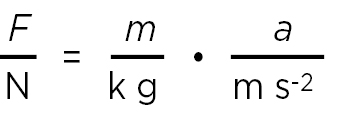 (3)
(3)
where {F}N = F/Nis the numerical value of the force in newtons, etc. Eq. (3) can be derived from (2) by division of both sides by N = kg m s–2.
If we measure the mass in pounds and acceleration in inches per second squared and we are still interested in the force in newtons, we can divide equation (2) by (lb in s–2) = 0.545 kg • 0.0254 m s–2 = 0.0115 N, obtaining
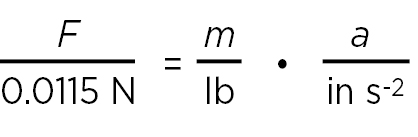
or, in a more convenient form,
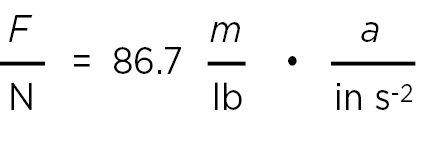 (4)
(4)
Quantity calculus is recommended for general use in science and technology. It has particular advantages in facilitating the problems of converting between different units and different systems of units, as exemplified above. Another important advantage of quantity calculus is that equations between quantities are independent of the choice of units, and must always satisfy the rule that the dimensions must be the same for each term on either side of the equal sign. The advantages are illustrated in several examples presented in the IUPAC Green Book (E. R. Cohen, T. Cvitas, J. G. Frey, B. Holmström, K. Kuchitsu, R. Marquardt, I. Mills, F. Pavese, M. Quack, J. Stohner, H. L. Strauss, M. Takami, and A. J. Thor. Quantities, Unit and Symbols in Physical Chemistry (IUPAC Green Book). IUPAC and RSC Publishing, Cambridge, 3rd edition, 2nd printing, 2008, page 131).
Professor Tomislav Cvitas is an emeritus professor from the University of Zagreb, in Croatia. A long time member of IUPAC, he is a former President of the Physical Chemistry Division and a former chair of the Interdivisional Committee on Terminology, Nomenclature and Symbols (ICTNS). He is a co-author of the IUPAC Green Book.
About NOTeS - This series, initiated in January 2014, is coordinated by the Interdivisional Committee on Terminology, Nomenclature and Symbols (ICTNS). Topics presented previously include: "On the Use of Italic and Roman Fonts for Symbols in Scientific Text" by Ian Mills (September 2014, p. 23), "Symbols of the Elements" by Juris Meija (January 2014, p.20), "Part II" (May 2014 issue, p, 18), "Part III" (concluded; July 2014, p. 25); and "The Units ppm, ppb, and ppt" by Ian Mills (March 2014, p. 23).
©2015 by Walter de Gruyter Berlin/Boston
Articles in the same Issue
- Masthead - Full issue pdf
- Oficer’s Column
- The First IUPAC Congress in Korea
- Features
- Books of Secrets: Writing & Reading Alchemy
- What's in a Name? Quite a Lot, as it Happens!
- Systematic Flexibility and the History of the IUPAC Nomenclature of Organic Chemistry
- IUPAC Wire
- Election of IUPAC Officers and Bureau Members – Call for Nominations
- Measurements and Light
- ICSU announces Dr. Heide Hackmann to be Executive Director and Dr. Lucilla Spini to be Head of Science Programmes
- The 2014 AAAS Award for Science Diplomacy goes to Zafra M. Lerman
- OPCW-The Hague Award Presented at 19th Conference of States Parties
- IUPAC Physical Chemistry Cartoon Competition 2015
- IUPAC Office move
- IUPAC Provisional Recommendations
- Glossary of Terms Used in Neurotoxicology
- Stamps International
- Otto Wichterle: An Eye for Hydrogels
- Making an ImPACt
- Immunochemical Recognition and its Diagnostic and Therapeutic Applications
- NOTeS
- On the Use of Quantity Calculus
- Conference Call
- Pesticide Chemistry
- Photobiology
- Solubility Phenomena and Related Equilibrium Processes
- Data Sharing for Sustainability
- Where 2B & Y
- Mark Your Calendar
Articles in the same Issue
- Masthead - Full issue pdf
- Oficer’s Column
- The First IUPAC Congress in Korea
- Features
- Books of Secrets: Writing & Reading Alchemy
- What's in a Name? Quite a Lot, as it Happens!
- Systematic Flexibility and the History of the IUPAC Nomenclature of Organic Chemistry
- IUPAC Wire
- Election of IUPAC Officers and Bureau Members – Call for Nominations
- Measurements and Light
- ICSU announces Dr. Heide Hackmann to be Executive Director and Dr. Lucilla Spini to be Head of Science Programmes
- The 2014 AAAS Award for Science Diplomacy goes to Zafra M. Lerman
- OPCW-The Hague Award Presented at 19th Conference of States Parties
- IUPAC Physical Chemistry Cartoon Competition 2015
- IUPAC Office move
- IUPAC Provisional Recommendations
- Glossary of Terms Used in Neurotoxicology
- Stamps International
- Otto Wichterle: An Eye for Hydrogels
- Making an ImPACt
- Immunochemical Recognition and its Diagnostic and Therapeutic Applications
- NOTeS
- On the Use of Quantity Calculus
- Conference Call
- Pesticide Chemistry
- Photobiology
- Solubility Phenomena and Related Equilibrium Processes
- Data Sharing for Sustainability
- Where 2B & Y
- Mark Your Calendar


