Abstract
This paper uses a new method for describing dynamic comovement and persistence in economic time series which builds on the contemporaneous forecast error method developed in den Haan [den Haan, W. J. 2000. “The Comovement between Output and Prices.” Journal of Monetary Economics 46: 3–30]. This data description method is then used to address issues in New Keynesian model performance in two ways. First, well known data patterns, such as output and inflation leads and lags and inflation persistence, are decomposed into forecast horizon components to give a more complete description of the data patterns. These results show that the well-known lead and lag patterns between output and inflation arise mostly in the medium-term forecasts horizons. Second, the data summary method is used to investigate a small-scale New Keynesian model with some important modeling features to see which of these features can reproduce lead, lag and persistence patterns seen in the data. We show that a general equilibrium model with habit formation, persistent IS curve shocks and persistent supply shocks can reproduce the lead, lag and persistence patterns seen in the data.
Acknowledgments
We are grateful for helpful comments from two anonymous referees, Arpad Abraham (the Editor), Mikel Casares, Javier Ferri, and seminar participants at 2010 Midwest Macroeconomics Meetings (East Lansing, Michigan), 2010 Computing in Economics and Finance Conference (London), 2012 SAEe (Vigo), Universidad del País Vasco, Universidad Pública de Navarra and Universidad de Murcia. Some of this research was supported by the Spanish Ministry of Education and Science, grant numbers SEJ2006-12793/ECON, SEJ2007-66592-C03-01-02/ECON and ECO2010-16970. 2006–2009, Basque Government grants IT-241-07 and GME0702. Cassou would also like to thank Ikerbasque for financial support.
Appendix A
Confidence Band Appendix
Figure A.1 shows the confidence bands associated with the contemporaneous and lead comovements between output and inflation which were displayed in Figure 2. This figure breaks apart some of the individual diagrams in Figure 2, so that only one plot is shown in each of the sub-figures. In particular, each of the sub-figures include either a contemporaneous or a lead plot from Figure 2 along with a 95% confidence intervals around the plot. The confidence bands where generated using a bootstrap method. As Figure A.1 shows, the confidence bands are quite wide and that the individual lead lines are not significantly different from the contemporaneous line. However, many individual correlations associated with alternative leads and forecast horizons are statistically significant whereas the contemporaneous correlation for the corresponding forecast horizon is not. Therefore, we still think that it is possible to interpret the leads and lags as we did in the paper. Such an interpretation is consistent with conclusions in Fuhrer and Moore (1995), Galí and Gertler (1999) and numerous others.
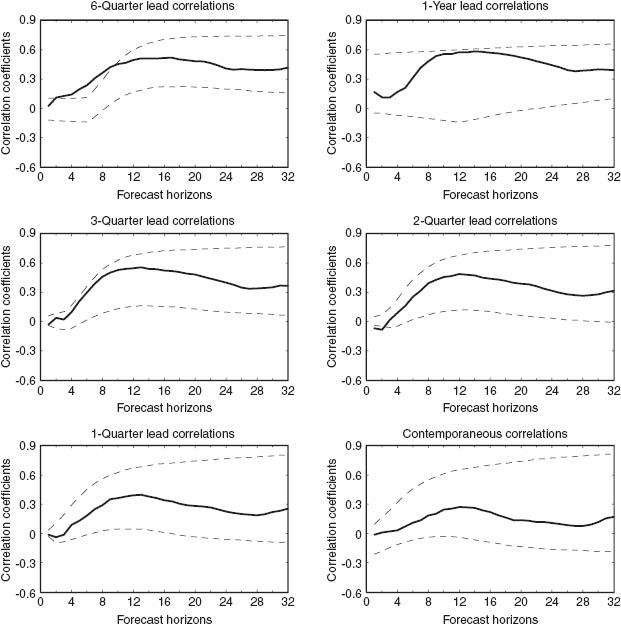
Comovement between Output and Inflation (confidence bands).
References
Buiter, W. H., and I. Jewitt. 1981. “Staggered Wage Setting with Real Wage Relativities: Variations on a Theme of Taylor.” The Manchester School 49: 211–228.10.1111/j.1467-9957.1981.tb00948.xSuche in Google Scholar
Calvo, G. A. 1983. “Staggered Prices in a Utility-maximizing Framework.” Journal of Monetary Economics 12: 383–398.10.1016/0304-3932(83)90060-0Suche in Google Scholar
Christiano, L. J., M. Eichenbaum, and C. L. Evans. 2005. “Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy.” Journal of Political Economy 113: 1–45.10.1086/426038Suche in Google Scholar
Coenen, G., and V. Wieland. 2005. “A Small Estimated Euro Area Model with Rational Expectations and Nominal Rigidities.” European Economic Review 49: 1081–1104.10.1016/j.euroecorev.2003.05.001Suche in Google Scholar
Cogley, T., and A. M. Sbordone. 2008. “Trend Inflation, Indexation, and Inflation Persistence in the New Keynesian Phillips Curve.” American Economic Review 98: 2101–2126.10.1257/aer.98.5.2101Suche in Google Scholar
den Haan, W. J. 2000. “The Comovement between Output and Prices.” Journal of Monetary Economics 46: 3–30.10.1016/S0304-3932(00)00016-7Suche in Google Scholar
den Haan, W. J., and S. W. Sumner. 2004. “The Comovement between Output and Prices in the G7.” European Economic Review 48: 1333–1347.10.1016/j.euroecorev.2003.05.002Suche in Google Scholar
Dossche, M., and G. Everaert. 2007. “Disentangling the Sources of Inflation Persistence.” Working Paper, National Bank of Belgium.Suche in Google Scholar
Fernández-Villaverde, J., and J. F. Rubio-Ramrez. 2004. “Comparing Dynamic Equilibrium Economies to Data: A Bayesian Approach.” Journal of Econometrics 123: 153–187.10.1016/j.jeconom.2003.10.031Suche in Google Scholar
Fuhrer, J. C. 1997. “The (Un)Importance of Forward-looking Behavior in Price Specifications.” Journal of Money, Credit, and Banking 29: 338–350.10.2307/2953698Suche in Google Scholar
Fuhrer, J. C. 2006. “Intrinsic and Inherited Inflation Persistence.” International Journal of Central Banking 2: 49–86.Suche in Google Scholar
Fuhrer, J. C., and G. R. Moore. 1995. “Inflation Persistence.” Quarterly Journal of Economics 440: 127–159.10.2307/2118513Suche in Google Scholar
Galí, J. 2003. New Perspectives on Monetary Policy, Inflation, and the Business Cycle. In<nonbrspace;Advances in Economic Theory, Vol. III, edited by M. Dewatripont, L. Hansen, and S. Turnovsky, 151–197. Cambridge: Cambridge University Press.10.1017/CBO9780511610264.007Suche in Google Scholar
Galí, J., and M. Gertler. 1999. “Inflation Dynamics: A Structural Econometric Analysis.” Journal of Monetary Economics 44: 195–222.10.1016/S0304-3932(99)00023-9Suche in Google Scholar
Hodrick, R. J., and E. C. Prescott. 1997. “Postwar U.S. Business Cycles: An Empirical Investigation.” Journal of Money, Credit and Banking 29: 1–16.10.2307/2953682Suche in Google Scholar
Ireland, P. N. 2004. “Technology Shocks in the New Keynesian Model.” Review of Economics and Statistics 86: 923–936.10.1162/0034653043125158Suche in Google Scholar
Ireland, P. N. 2007. “Changes in the Federal Reserve’s Inflation Target: Causes and Consequences.” Journal of Money, Credit, and Banking 39: 1851–1882.10.1111/j.1538-4616.2007.00091.xSuche in Google Scholar
Keen, B. D. 2009. “Output, Inflation, and Interest Rates in an Estimated Optimizing Model of Monetary Policy.” Review of Economic Dynamics 12: 327–343.10.1016/j.red.2008.08.003Suche in Google Scholar
Lansing, K. 2009. “Time-varying U.S. Inflation Dynamics and the New Keynesian Phillips Curve.” Review of Economic Dynamics 12: 304–326.10.1016/j.red.2008.07.002Suche in Google Scholar
Lubik, T. A., and F. Schorfheide. 2003. “Computing Sunspot Equilibria in Linear Rational Expectations Models.” Journal of Economic Dynamics and Control 28: 273–285.10.1016/S0165-1889(02)00153-7Suche in Google Scholar
Lubik, T. A., and F. Schorfheide. 2004. “Testing for Indeterminacy: An Application to U.S. Monetary Policy.” American Economic Review 94: 190–217.10.1257/000282804322970760Suche in Google Scholar
Mankiw, N. G. 2003. Macroeconomics. New York: Worth Publishers.Suche in Google Scholar
María-Dolores, R., and J. Vázquez. 2008. “The New Keynesian Monetary Model: Does it Show the Comovement between GDP and Inflation in the U.S.?” Journal of Economic Dynamics and Control 32: 1466–1488.10.1016/j.jedc.2007.06.002Suche in Google Scholar
Rotemberg, J. J., and M. Woodford. 1997. “An Optimization-based Econometric Framework for the Evaluation of Monetary Policy.” In NBER Macroeconomics Annual 1997, edited by Ben S. Bernanke and Julio J. Rotemberg, 297–346. Cambridge, MA: MIT Press.10.1086/654340Suche in Google Scholar
Rudd, J., and K. Whelan. 2006. “Can Rational Expectations Sticky-price Models Explain Inflation Dynamics?” American Economic Review 96: 303–320.10.1257/000282806776157560Suche in Google Scholar
Sargent, T. J., and P. Surico. 2011. “Two illustrations of the Quantity Theory of Money: Breakdowns and Revivals.” American Economic Review 101: 109–128.10.1257/aer.101.1.109Suche in Google Scholar
Sims, C. A. 2002. “Solving Linear Rational Expectations Models.” Computational Economics 20: 1–20.10.1023/A:1020517101123Suche in Google Scholar
Smets, F., and R. Wouters. 2003. “An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area.” Journal of the European Economic Association 1: 1123–1175.10.1162/154247603770383415Suche in Google Scholar
Smets, F., and R. Wouters. 2007. “Shocks and Frictions in the U.S. Business Cycles: A Bayesian DSGE Approach.” American Economic Review 97: 586–606.10.1257/aer.97.3.586Suche in Google Scholar
Taylor, J. B. 1980. “Aggregate Dynamics and Staggered Contracts.” Journal of Political Economy 88: 1–24.10.1086/260845Suche in Google Scholar
Walsh, C. E. 2003. Monetary Theory and Policy. Cambridge, Massachusetts: The MIT Press.Suche in Google Scholar
©2014 by De Gruyter
Artikel in diesem Heft
- Frontmatter
- Advances
- Optimal portfolios with wealth-varying risk aversion in the neoclassical growth model
- Inventories and the stockout constraint in general equilibrium
- Optimal second best taxation of addictive goods in dynamic general equilibrium: a revenue raising perspective
- Inflation effects on capital accumulation in a model with residential and non-residential assets
- Optimal capital-income taxation in a model with credit frictions
- Contributions
- Interest rate fluctuations and equilibrium in the housing market
- News shocks and learning-by-doing
- Capacity utilization and the effects of energy price increases in Japan
- Small-scale New Keynesian model features that can reproduce lead, lag and persistence patterns
- Optimal policy and Taylor rule cross-checking under parameter uncertainty
- The impact of American and British involvement in Afghanistan and Iraq on health spending, military spending and economic growth
- Why does natural resource abundance not always lead to better outcomes? Limited financial development versus political impatience
- The skill bias of technological change and the evolution of the skill premium in the US since 1970
- Aggregate impacts of recent US natural gas trends
- Organizational learning and optimal fiscal and monetary policy
- Industrial specialization, financial integration and international consumption risk sharing
- Leverage, investment, and optimal monetary policy
- Public debt in an OLG model with imperfect competition: long-run effects of austerity programs and changes in the growth rate
- Temporal aggregation and estimated monetary policy rules
- International transmission of productivity shocks with nonzero net foreign debt
- Did the euro change the effect of fundamentals on growth and uncertainty?
- Topics
- Real factor prices and factor-augmenting technical change
- Monetary policy and TIPS yields before the crisis
Artikel in diesem Heft
- Frontmatter
- Advances
- Optimal portfolios with wealth-varying risk aversion in the neoclassical growth model
- Inventories and the stockout constraint in general equilibrium
- Optimal second best taxation of addictive goods in dynamic general equilibrium: a revenue raising perspective
- Inflation effects on capital accumulation in a model with residential and non-residential assets
- Optimal capital-income taxation in a model with credit frictions
- Contributions
- Interest rate fluctuations and equilibrium in the housing market
- News shocks and learning-by-doing
- Capacity utilization and the effects of energy price increases in Japan
- Small-scale New Keynesian model features that can reproduce lead, lag and persistence patterns
- Optimal policy and Taylor rule cross-checking under parameter uncertainty
- The impact of American and British involvement in Afghanistan and Iraq on health spending, military spending and economic growth
- Why does natural resource abundance not always lead to better outcomes? Limited financial development versus political impatience
- The skill bias of technological change and the evolution of the skill premium in the US since 1970
- Aggregate impacts of recent US natural gas trends
- Organizational learning and optimal fiscal and monetary policy
- Industrial specialization, financial integration and international consumption risk sharing
- Leverage, investment, and optimal monetary policy
- Public debt in an OLG model with imperfect competition: long-run effects of austerity programs and changes in the growth rate
- Temporal aggregation and estimated monetary policy rules
- International transmission of productivity shocks with nonzero net foreign debt
- Did the euro change the effect of fundamentals on growth and uncertainty?
- Topics
- Real factor prices and factor-augmenting technical change
- Monetary policy and TIPS yields before the crisis

