Abstract
The article describes the way to calculate the distances, defined by the U.S. Federal Aviation Administration in the AC 70-1B document, essential for the flight safety in the case of illumination of aircraft pilots by laser radiation. FAA’s calculations and presented examples are simplified for the most common cases of a single circular beam, or circular beams sharing the same power, divergence and aperture. Proposed in this article calculation method was extended to multi-beam radiation sources characterized by different wavelengths, different divergences in two perpendicular planes and different powers. The impact of ellipticity of the beams on the calculated distances was shown. The presented analysis may be a supplement to the AC 70-1B document and may serve as a sample approach for those who need to deal with such laser sources. Laser pointers characterized by powers of up to 50 W as well as these with typical powers of several mW were considered. It was shown that even typical 1 mW laser pointers may still distract the aircraft pilots during landing or take-off which may have adverse consequences.
1 Introduction
Scientific and technological progress is becoming more and more noticed by every person. More and more newly developed devices reach the market very quickly and are available to almost everyone. The price barrier that may limit access to certain technological developments is increasingly disappearing, in particular in rich, highly developed countries. This phenomenon is also noticeable in the field of laser devices. On the market, it is possible to buy such devices emitting radiation of relatively high powers for little money. Worth attention are laser pointers emitting visible radiation in the green, blue and red wavelength band [1], [2], [3], [4]. Pointers of relatively low power, reaching a few milliwatts, are intended to be used by speakers as a pointing tool during lectures or presentations. However, their irrational use for entertainment and fun purposes is more and more often noticed, which in consequence may even lead to eye damage, especially among children [5], [6], [7], [8], [9], [10], [11], [12], [13], [14]. Each laser device should be assigned to the appropriate safety class, which should impose its appropriate handling, but this is not always the case [15]. Recently, so-called laser pointers with powers reaching several dozen Watts, which are actually high power laser sources, have appeared [16]. Such sources, in particular, pose a very high risk to the human eye.
Misuse of laser pointers to illuminate landing or taking off aircraft deserves special attention. In recent years, there are more and more reports of such use, which can interfere with law enforcement and rescue missions, and infrequently leads to a ‘go-around’ on a landing attempt. In 2021, pilots reported 9,723 incidents related to laser illumination to the U.S. Federal Aviation Administration [17]. Therefore, as early as the 1990s, experts began working to establish certain guidelines determining what level of exposure to radiation is safe and how much may pose a threat to safety. On the basis of some tests done, with the help of volunteers, by G10T Laser Safety Hazards Committee of Society of Automotive Engineers (SAE), and somewhat by discussions and negotiations, the experts defined three levels of exposure in the AS4970 standard [18]. These exposure levels were accepted and published by the U.S. Federal Aviation Administration in its Advisory Circular 70-1 (revised Feb. 14 2022 to AC 70-1B[1]) [19]. The levels are:
Greater than 100 μW/cm2 – an exposure that may cause potential eye injury and temporary flashblindness with resulting afterimages.
From 5 μW/cm2 to 100 μW/cm2 – An exposure that may cause veiling (obscuring) glare.
From 50 nW/cm to 5 μW/cm2 – An exposure that does not interfere with vision but which may cause distraction.
Exposures of less than 50 nW/cm2 are not expected to be brighter than most city or airport lights at night and thus are not expected to cause distraction.
Moreover, in this document four different distances from the source of laser radiation were defined:
Nominal Ocular Hazard Distance (NOHD) – Beyond this distance the beam is the Maximum Permissible Exposure (MPE) or less. The beam is an eye hazard from the laser source to this distance. The values of MPE depends on wavelength and time of exposure and are tabulated in well-known standards ANSI Z136.1 about safe use of lasers [20], and IEC 60825-1 about safety of laser products [21].
Sensitive Zone Exposure Distance (SZED) – Beyond this distance, the beam irradiance is 100 μW/cm2 or less. Between the NOHD and the SZED, the beam can cause temporary flashblindness with resulting afterimages.
Critical Zone Exposure Distance (CZED) – Beyond this distance, the beam irradiance is 5 μW/cm2 or less. Between the SZED and the CZED the beam may cause veiling (obscuring) glare.
“Laser-Free” Exposure Distance (LFED) – Beyond this distance the beam irradiance is 50 nW/cm2 or less. Between the CZED and the LFED the beam appears brighter than most city or airport lights at night and thus may distract a pilot. Beyond the LFED the beam is not expected to cause distraction.
Following the law of most countries, any proponents planning to conduct outdoor laser operations that may affect aircraft operations should file a special notice with the appropriate Aviation Agency such as FAA before the planned event. All the above mentioned distances are usually needed to be calculated and entered into this notice. To calculate them may not seem to be tricky task, especially that there are some examples in AC 70-1B as well as on some webpages [22]. However, FAA’s calculations and presented examples are simplified for the most common cases of a single circular beam, or circular beams sharing the same power, divergence and aperture. In the new AC 70-1B FAA does provide examples of multi-beam analysis, which was first proposed in [23]. However FAA has always allowed proponents to submit a more complex, alternative analysis as long as it is based on ANSI Z136 or other established methods, and as long as the methods and calculations are documented. The aim of this article is to describe how the standard, non-simplified NOHD calculation can be used for complex cases of multi-beam laser radiation characterized by different wavelengths, different divergences in two perpendicular planes and different powers. Both FAA’s AC 70-1B and this paper assume that the beam diameters at the exit aperture are relatively small compared to the diameters at the exposure site. FAA specifically states its simplified equations are valid for diameters 1 cm or less at the output aperture [see footnote 5 on AC 70-1B page A-16].
2 Calculation of NOHD, SZED, CZED and LFED for multi-beam radiation
The values of NOHD, for a single beam of given power or energy, divergence and diameter at the output aperture, can be easily calculated using the well-known equation:
where:
H –power or energy of the beam,
∅– divergence,
w – diameter of the beam at the output aperture
tg – tangent.
For many beams that can be emitted out of the same aperture in the same direction, characterized by different powers and wavelengths as well as different divergences in two perpendicular planes (elliptical cross-section), the calculation becomes a little more complex. If the beams don’t affect the same tissue they can be treated independently and calculation can be carried out separately for each of the beams. Then, the most relevant beam, from the safety point of view, is the one for which the most restrictive results were obtained. However if the beams affect the same tissue they can’t be treated independently. They should be treated additively. In the case of visible radiation, which is in the range of 400–700 nm, it affects the same tissue (retina of the eye). Different beams from this band contribute to the creation of a visual effect to an extent proportional to the ratio of the exposure level to the level necessary for creation of this effect for a given wavelength. Thus, to create this visual effect the sum of these ratios for all beams should be equal to 1. In the case of n beams of different wavelengths the additivity effect can be expressed in the following form:
where:
El – exposure level (expressed as power or energy per area of exposed tissue).
In the above equation the MPE represents the exposure level at which the risk of eye damage is increased for each of the beams.
Going through some not complicated calculation (presented in more details in [24]), for beams with elliptical cross-section (two different divergences in two planes) and assuming that diameters of the beams at the exit aperture are relatively small compared to the diameters at the exposure site (which is the case for most cases), Eq. (2) can be written as:
where:
P – power of a beam,
ϕ x – angle of divergence in x plane,
ϕ y – angle of divergence in y plane.
In the above equation, instead of the power the energy of the beam can be used, however in that case, the MPE expressed in W/m2 should be changed into J/m2 for an appropriate exposure time.
According to the standards [20, 21], the aversion response, which takes into account closure of the eyelid, eye movements, pupillary constriction, or movement of the head to avoid an exposure to a noxious or bright light stimulant, was agreed to be equal to 0.25 s, thus the eye exposure time to visible radiation can be assumed to be equal to this value. However it should also be noted that there is some research that perhaps the 0.25 s aversion response time should be re-evaluated [25]. Apart from this, following the standards, MPE for radiation in the visible wavelength band of 400–700 nm and exposure time of 0.25 s is the same. Thus, assuming that most laser sources are characterized by small divergence (up to several milliradians) Eq. (3) can be transformed to:
Similar equations can be derived for SZED, CZED and LFED. However, besides the change of MPE into appropriate exposure levels defined for each of these distances, the power of the beams has to be corrected by multiplying it by Visual Correction Factor defined for different wavelengths (VCF (λ)). The additivity of spectral sensitivity of the eye for visible radiation can be here assumed again, however it has not been firmly proven for laser exposure [26, 27].
The values of VCF (λ) in the band of 400–700 nm were tabulated in AC 70-1B with 5 nm step (for 555 nm VCF (λ) = 1) [19]. According to the guidelines included in the AC 70-1B, if a wavelength falls between two table entries the conservative approach can be applied and thus the more restrictive (larger) value of the two resulting VCF (λ) should be used.
The values of VCF (λ), with smaller step of 0.1 nm, were also published by The Color & Vision Research laboratory based at the Institute of Ophthalmology, which is part of University College London and were adopted by International Commission on Illumination (CIE) in its report CIE 170-1:2006 [28]. Its tabulated values can be found in databases available online [29]. The values of VCF (λ) presented in these databases result from research into human cone spectral sensitivities and luminous efficiency. They provide a consistent set of colorimetric and photometric data that can be used to model and predict normal and dichromatic color vision for standard target sizes of 2-deg or 10-deg in diameter.
In Table 1 the exposure levels, defined for the analyzed distances, are presented. The values of VCF (λ) accepted by FAA and CIE (2-deg Luminous Efficiency Function) for some wavelengths, that can be generated by most typical laser sources, especially used as pointers, are shown in Table 2. One can see some difference between the values assumed by FAA and CIE. Generally they are lower for FAA. Higher values for FAA may be achieved for wavelengths that fall between two table entries defined in AC 70-1B as a result of using more restrictive (larger) value of the two. Also, a higher value is achieved for FAA at the wavelength close to 555 nm because the VCF (λ) = 1 is assumed to be at 556.1 nm for CIE. In most cases the differences result in shorter distances calculated for FAA VCF (λ) values.
| Distance | Value [W/m2] | Reference |
|---|---|---|
| NOHD | 25.46 | IEC 60825-1, ANSI Z136.1 |
| 26.0 | AC 70-1B | |
| SZED | 1 | AS4970, AC 70-1B |
| CZED | 5·10−2 | AS4970, AC 70-1B |
| LFED | 5·10−4 | AS4970, AC 70-1B |
| Wavelength [nm] | 400 | 405 | 445 | 450 | 455 | 520 | 525 |
|---|---|---|---|---|---|---|---|
| VCF (λ) (CIE) | 0.0025 | 0.0050 | 0.0574 | 0.0647 | 0.0724 | 0.7181 | 0.7946 |
| VCF (λ) (FAA) | 0.0004 | 0.0008 | 0.0305 | 0.0380 | 0.0490 | 0.7092 | 0.7857 |
| Wavelength [nm] | 532 | 555 | 556.1 | 635 | 638 | 650 | 700 |
| VCF (λ) (CIE) | 0.8783 | 0.9995 | 1.0 | 0.2417 | 0.2122 | 0.1193 | 0.0042 |
| VCF (λ) (FAA) | 0.9073 | 1.0 | 1.0 | 0.2202 | 0.2202 | 0.1070 | 0.0041 |
For laser/aviation safety, the values of VCF (λ) as well as exposure levels presented in AC 70-1B should be used, at least in the U.S., since the law and regulation are based on them. Subsequent calculations described in this article use these values.
Applying the defined maximum permissible exposures the respective distances can be determined with the help of the following equations:
One can see that only the NOHD and the SZED needs to be calculated using Eqs. (5) and (6). Due to the constants in the equations, the CZED will always be around 4.473 times the SZED, and the LFED will always be around 44.73 times the SZED. Such assumption is also made in AC 70-1B.
3 Analysis of NOHD, SZED, CZED and LFED for different laser sources
The most common sources of radiation applied in laser pointers are laser diodes that are characterized by many useful features. One of them is the price that makes the laser pointers available for almost everyone. Other features worth mentioning are low weight, small dimensions as well as rigid and compact design that makes the laser pointers particularly resistant to temperature changes and shocks. Moreover they are able to generate cw powers of up to several watts from a structure embedded in a typical TO9 housing. Good examples are those produced by Nichia (emitting blue and green radiation) [30] and Ushio (emitting red radiation) [31].
One of the main disadvantages of laser diodes is the divergence of the laser beam they generate, which can reach even several dozen degrees. Moreover, the power distribution in cross-section of the beam is usually elliptical. However, these disadvantages can be remedied in a relatively simple manner by means of appropriately designed optics. Applying laser diodes many different laser pointers as well as modules, with the possibility to be used as laser pointers, were developed and released on the market. In Table 3 some example laser pointers and laser modules of relatively high power, with parameters defined by their manufacturers, are shown. The first three positions in the table are laser sources that can emit radiation of three colors at the same time. The rest emit beams of single wavelength.
Example laser pointers and laser modules.
| Laser pointers and modules | Wavelength [nm] | Power [W] | Divergence x [mrad] | Divergence y [mrad] | Ref. |
|---|---|---|---|---|---|
| RGB 7 colors laser pointer LM-680 | 650 | 0.15 | – | – | [2], [3], [4] |
| 520 | 0.1 | – | – | ||
| 450 | 0.1 | – | – | ||
| RGB handheld laser pointer | 635 | 0.2 | – | – | [1] |
| 525 | 0.13 | – | – | ||
| 455 | 0.17 | – | – | ||
| 4 W RGB laser module | 638 | 1.1 | 1.8 | 1.8 | [32] |
| 520 | 1 | ||||
| 445 | 2 | ||||
| Laser pointer G32000350 | 638 | 50 | – | – | [16] |
| Laser pointer G32000349 | 520 | 50 | – | – | [16] |
| Laser pointer G32000080 | 450 | 50 | 1.5 | 1.5 | [16] |
| Laser pointer 32007040 | 650 | 30 | – | – | [16] |
| Laser pointer G32000077 | 520 | 30 | 1.5 | 1.5 | [16] |
| Laser pointer G32000079 | 450 | 30 | 1.5 | 1.5 | [16] |
| Laser module R638-700SM | 638 | 0.7 | 5 | 5 | [32] |
| Laser module G520-1000SM | 520 | 1 | 3 | 3 | [32] |
| Laser module B445-4000CM | 445 | 4 | 2.5 | 2.5 | [32] |
For the above presented laser sources the distances NOHD, SZED, CZED and LFED applying Eqs. (5)–(8) were calculated. For the divergence not defined by the manufacturer the value of 1.5 mrad was assumed. The results of the calculations are shown in Figures 1, 2, 3, 4, 5, and 6. For lasers emitting in the visible range 400–700 nm, the values of NOHD depend only on power and divergence of the beam so for pointers of the same power and divergence they are also the same and are equal to 1043 m for 50 W pointers and 808 m for 30 W pointers. The values of SZED, CZED and LFED strongly depend on wavelength therefore they are so different for the pointers of the same power and divergence. Analyzing the results shown in Figure 1 one can see that even for powers as small as 100 mW all the distances are relatively long. The highest values are achieved for wavelength of 520 nm reaching almost 9 km for LFED. For wavelength of 650 and 450 nm the distances are much shorter however they are still long enough to cause problems for a pilot especially if the plane is landing. At a distance up to several dozen meters the pilot would be within the NOHD, although there are factors such as the laser being handheld and the aircraft moving which make injury much less likely than in a laboratory test setting.

NOHD, SZED, CZED and LFED calculated for RGB 7 colors laser pointer LM-680.

NOHD, SZED, CZED and LFED calculated for RGB handheld laser pointer.

NOHD, SZED, CZED and LFED calculated for 4 W RGB laser module.
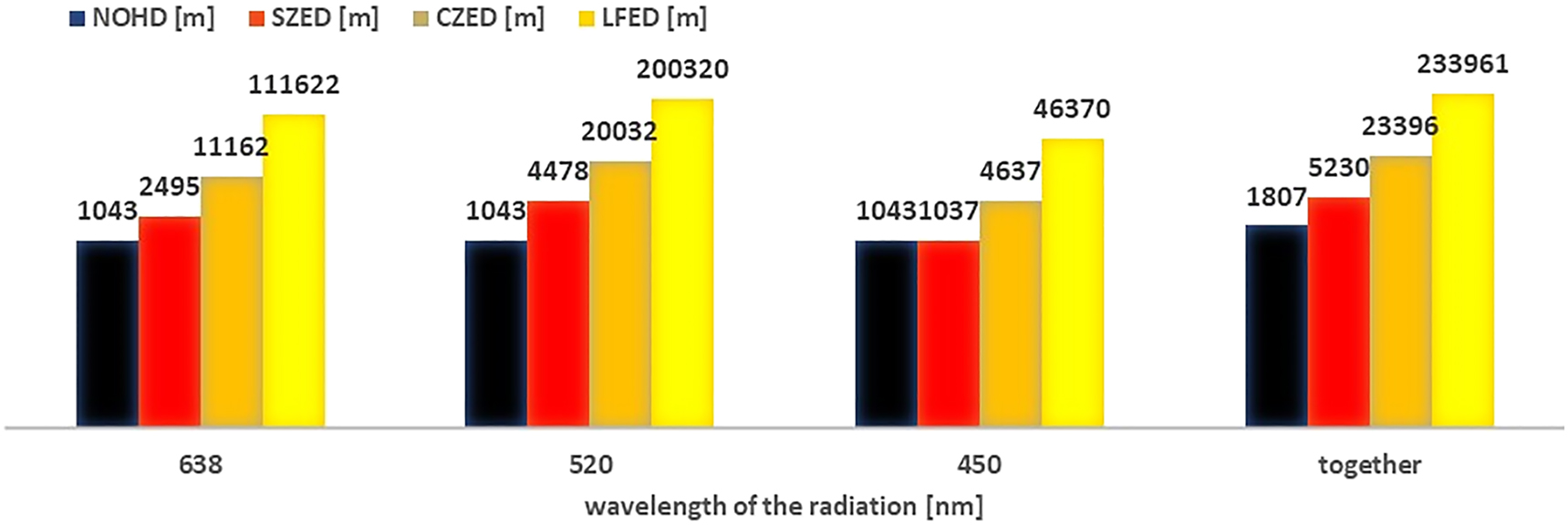
NOHD, SZED, CZED and LFED calculated for laser pointers of 50 W output power.

NOHD, SZED, CZED and LFED calculated for laser pointers of 30 W output power.

NOHD, SZED, CZED and LFED calculated for laser modules R638-700SM, G520-1000SM and B445-4000CM.
Considering the additivity of the laser beams the relatively highest increase in distance is for NOHD. For 50 W pointer it reaches over 1.8 km for three beams while for a single beam it is over 1 km. In the case of SZED, CZED and LFED the increase is not so high in relation to the green beam. It is mainly caused by the small values of VCF (λ) for red and blue wavelengths. For 50 W pointers the LFED distance increased by more than 33 km reaching almost 234 km.
At most wavelengths, for the same pointer, the shortest distances are achieved for NOHD while they gradually increase for SZED, CZED and LFED. Such behavior is caused by the respective gradual decrease of the defined maximum permissible exposures. However it is not always the case.
For any visible wavelength less than 450.6 nm, or greater than 667.4 nm, the values for the NOHD will be higher than the values for the SZED. It means that for these wavelength ranges, the SZED temporary visual impairment of flashblindness/afterimage is accompanied by a potential for eye damage, e.g., being within the NOHD. Moreover these wavelength ranges do not depend on the power or divergence of the beam. The SZED will always be less than the NOHD for ANY visible wavelength <450.6 nm or >667.4 nm.
It is also possible for the CZED to be less than the NOHD for any visible wavelength <412.8 nm. The values of LFED will always be higher than the NOHD for the whole spectrum of visible radiation. The values of NOHD, SZED and CZED in function of wavelength for radiation source emitting a beam with a power of 1 W and a divergence of 1.5 mrad in both perpendicular planes are shown in Figure 7.

NOHD, SZED and CZED in function of wavelength for radiation source emitting a beam with a power of 1 W and a divergence of 1.5 mrad in both perpendicular planes.
Considering the additivity of the beams, for some configuration of the wavelengths, divergences and powers the value of NOHD may also be higher than that of SZED and CZED, however, again, the values of LFED will be higher than that of NOHD for the whole spectrum of visible radiation.
On the market most laser pointers are characterized by relatively low power of around several mW. They are usually used by speakers during presentation, so many people tend to think that they are safe. To show the potential hazard of using such laser pointers, the calculation of the NOHD, SZED, CZED and LFED as a function of power up to 10 mW was done. The wavelength of 650, 532 and 405 nm, and a divergence of 1.5 mrad in both perpendicular planes, which are typical for many laser pointers, were assumed. The results of calculations are shown in Figures 8, 9, 10, 11, 12, and 13.

NOHD, SZED, CZED and LFED as a function of beam power for 650 nm wavelength and divergence of 1.5 mrad.
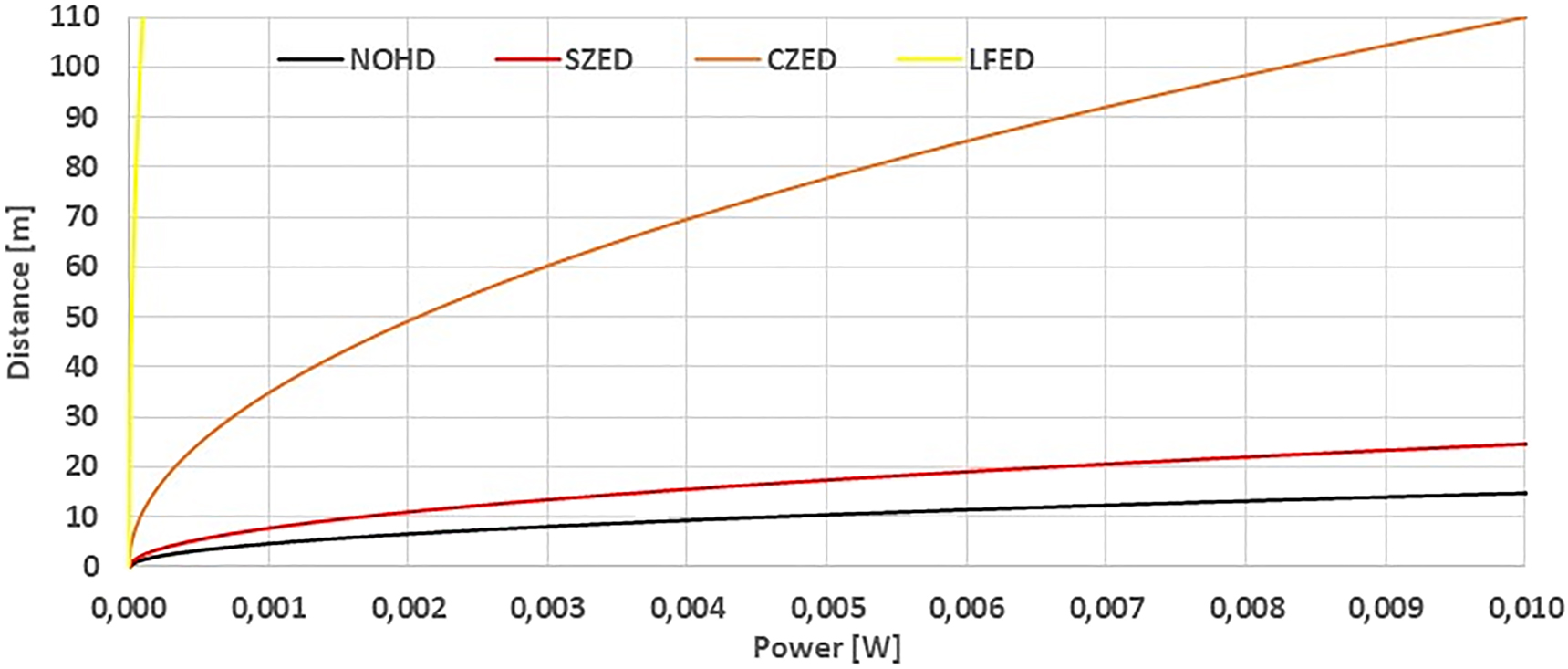
Same as the previous figure, but zoomed in 10× on the distance scale, to better show the relationships of the NOHD, SZED and CZED.

NOHD, SZED, CZED and LFED as a function of beam power for 532 nm wavelength and divergence of 1.5 mrad.

Same as the previous figure, but zoomed in 10× on the distance scale, to better show the relationships of the NOHD, SZED and CZED.

NOHD, SZED, CZED and LFED as a function of beam power for 405 nm wavelength and divergence of 1.5 mrad.

Same as the previous figure, but zoomed in 10× on the distance scale, to better show the relationships of the NOHD, SZED and CZED.
Presented results show that the NOHD is identical for the three wavelengths analyzed (650, 532 and 405 nm). For the visual interference distances SZED, CZED and LFED, the longest distances are obtained for the 532 wavelength. This is because of the three wavelengths analyzed, the 532 wavelength is closest to 555 nm, the wavelength with the highest VCF meaning it appears brightest to the human eye. Class 2 lasers are defined as lasers emitting visible light of up to1 mW power. These are generally considered safe for an exposure of less than 0.25 s. However there is a risk of eye damage. For example, the NOHD of a 1 mW laser with a 1.5 mrad divergence, for a 0.25 s exposure is 4.7 m. For any power change, the NOHD will increase or decrease by the square root of the power increase or decrease. For example, increasing a laser’s power 10 times will increase the NOHD by 3.16 times.
Contrasting this with an equivalent laser 10 times more powerful (10 mW) one can see that it has an NOHD over three times longer: 14.8 m. The distances SZED, CZED and LFED for 532 nm are equal to around 22.7 m, 101.3 m, 1013.3 m for 1 mW and 71.6 m, 320.4 m, 3204.3 m for 10 mW. This means that a 1 mW laser pointer emitting radiation with a wavelength of 532 nm and a beam divergence of 1.5 mrad can cause distraction of the aircraft pilot at a distance of around 1 km, while for 10 mW laser pointer this distance reaches more than 3 km.
For the wavelength of 650 and 405 nm, the NOHD distance is the same as for the 532 nm wavelength, while the other distances are much smaller. Nevertheless, laser pointers emitting such radiation can still pose a risk to airplane pilots. For the wavelength of 650 nm, the LFED distance is about 348 m for a power of 1 mW and 1100 m for a power of 10 mW, while for the wavelength of 405 nm, the LFED distance is about 30 m for a power of 1 mW and 95 m for a power of 10 mW. The values of NOHD, SZED, CZED and LFED for the beam with wavelength of 650 nm, 532 and 405 nm, divergences of 1.5 mrad in both perpendicular planes and power of 1 and 10 mW are summarized in Table 4.
NOHD, SZED, CZED and LFED for the beam with wavelength of 650 nm, 532 and 405 nm, divergences of 1.5 mrad in both perpendicular planes and power of 1 and 10 mW.
| Power [mW] | Distance [m] | Wavelength [nm] | ||
|---|---|---|---|---|
| 650 | 532 | 405 | ||
| 1 | NOHD | 4.7 | 4.7 | 4.7 |
| SZED | 7.8 | 22.7 | 0.7 | |
| CZED | 34.8 | 101.3 | 3.0 | |
| LFED | 348.0 | 1013.3 | 30.1 | |
| 10 | NOHD | 14.8 | 14.8 | 14.8 |
| SZED | 24.6 | 71.6 | 2.1 | |
| CZED | 110.0 | 320.4 | 9.5 | |
| LFED | 1100.4 | 3204.3 | 95.1 | |
The above analysis was carried out for beams with a circular cross-section. To show the influence of ellipticity on the distances appropriate calculations were carried out. The analysis was performed for laser pointers of 50 W output power and for low power laser pointers analyzed in the previous paragraphs. The beam divergence was assumed to be 1.5 mrad in perpendicular plane, and twice as large in the other perpendicular plane, amounting to 3 mrad. Figure 14 shows the results of the analysis for laser pointers of 50 W output power, and Table 5 for low power laser pointers.

NOHD, SZED, CZED and LFED calculated for laser pointers of 50 W output power and divergences of 1.5 mrad in one perpendicular plane and 3 mrad in the other perpendicular plane.
NOHD, SZED, CZED and LFED for the beam with wavelength of 650 nm, 532 and 405 nm, power of 1 and 10 mW and divergences of 1.5 mrad in one perpendicular plane and 3 mrad in the other perpendicular plane.
| Power [mW] | Distance [m] | Wavelength [nm] | ||
|---|---|---|---|---|
| 650 | 532 | 405 | ||
| 1 | NOHD | 3.3 | 3.3 | 3.3 |
| SZED | 5.5 | 16.0 | 0.5 | |
| CZED | 24.6 | 71.7 | 2.1 | |
| LFED | 246.1 | 716.5 | 21.3 | |
| 10 | NOHD | 10.4 | 10.4 | 10.4 |
| SZED | 17.4 | 50.6 | 1.5 | |
| CZED | 77.8 | 226.6 | 6.7 | |
| LFED | 778.1 | 2265.8 | 67.3 | |
Comparing the results shown in Figure 4 with the results in Figure 14, it can be seen that the values of all distances decreased
The influence of ellipticity

NOHD, SZED, CZED and LFED in function of ellipticity for laser pointer of 532 nm wavelength and 1 mW output power for long distances.

Same as the previous figure, but zoomed in 10× on the distance scale, to better show the relationships of the NOHD, SZED and CZED.

Same as the previous figure, but zoomed in about then 4× on the distance scale, to better show the relationships of the NOHD and SZED.

NOHD, SZED, CZED and LFED in function of ellipticity for system consisting of three laser pointers of 50 W output power for long distances.

Same as the previous figure, but zoomed in 10× on the distance scale, to better show the relationships of the NOHD, SZED and CZED.

Same as the previous figure, but zoomed in about then 4× on the distance scale, to better show the relationships of the NOHD and SZED.
The presented characteristics show that the distances decrease
4 Additional consideration
The presented analysis show the calculation of the distances essential for the safety of people especially those traveling by planes. The proposed calculations show how to determine these distances in the case of multi-beam laser sources. In the case of green, red and blue wavelengths of equal power and divergence, the green beam is characterized by the longest visual interference distances. However, the red and blue beams should not be forgotten. Even though their contributions to the calculated distances in the case of multi-beam radiation are not very high the presented calculation may be helpful if the accurate determination of the distance is important especially in court. It was shown that at wavelengths around 450.6 and 667.4 nm the values of SZED equal the values of NOHD. For shorter wavelengths than 450.6 nm and longer than 667.4 nm the SZED distance is shorter than NOHD, which means that at some distance intervals eye damage may occur before temporal vision impairment. The presented analysis also showed that typical low power laser pointers can cause safety concerns even for such powers as 1 mW. The calculations show that 532 nm laser pointer with power of 1 mW and divergence of 1.5 mrad may cause distraction at the distance of over 1 km. It means that aircraft pilot can be distracted during landing or taking off, which may have adverse consequences. For a power of 10 mW the distraction distance reaches more than 3 km. Other typical laser pointers operating in red or blue wavelength band may also cause safety concerns. Calculations and examples presented in the AC 70-1B document are simplified for the most common cases of a single circular beam, or circular beams sharing the same power, divergence and aperture. To overcome this limitation the article proposed the standard, non-simplified calculation of the defined distances that can be used for complex cases of multi-beam laser radiation characterized by different wavelengths, different divergences in two perpendicular planes and different powers. It may serve as an supplement to the AC 70-1B document and be a sample approach for dealing with such radiation sources.
The proposed way of determining the distances is not limited by the number of the beams that are considered. However there are some limitations to the calculations. First of all it was assumed that the beams travel in the same direction and have common optical axis. Secondly the intensity distribution in the cross-section of the beam was assumed to be Gaussian. Moreover the atmospheric attenuation was not taken into account. It can be expected that in a real environment the distances would be somewhat shorter which means that the radiation would not be so dangerous. However from the safety point of view if the attenuation of the atmosphere is not exactly known the best approach is to assume it be equal 0. Additionally, the results presented in the article concerns only laser sources that generate continuous wave (cw) radiation. However the calculations of the distances can be expanded to single pulse or repetitively pulsed sources. In the case of the NOHD it can be done by applying appropriate values of MPE for the right exposure time according to the standard [20, 21]. In case of other distances the situation is not so simple, however there are some guidelines in AC 70-1B [19] that can be followed. Last but not least, it would be useful to explore the vision impairment additivity assumption experimentally, i.e. exploring whether the human perception of multiple lasers does actually equal the effect calculated by simply adding the visually corrected power of beams to appropriate exposure levels ratios, as was done in this article. The mentioned limitations may be the subject of further work on the problem of illumination of aircraft pilots by laser radiation.
-
Author contributions: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.
-
Research funding: None declared.
-
Conflict of interest statement: The authors declare no conflicts of interest regarding this article.
References
[1] https://www.sanwulasers.com/.Search in Google Scholar
[2] https://www.burninglaserpointer.com/.Search in Google Scholar
[3] https://www.htpow.com/.Search in Google Scholar
[4] https://www.laserpointerstore.com/.Search in Google Scholar
[5] N. Raoof, T. K. J. Chan, N. K. Rogers, et al., “Toy’ laser macular burns in children,” Eye, vol. 28, pp. 231–234, 2014, https://doi.org/10.1038/eye.2013.315.Search in Google Scholar PubMed PubMed Central
[6] D. B. Gosling, J. B. O’Hagan, and F. M. Quhill, “Blue laser induced retinal injury in a commercial pilot at 1300 ft,” Aerosp Med Hum Perform, vol. 87, pp. 69–70, 2016, https://doi.org/10.3357/amhp.4411.2016.Search in Google Scholar
[7] J. Marshall, J. B. O’Hagan, and J. R. Tyrer, “Eye hazards of laser ‘pointers’ in perspective,” Br. J. Ophthalmol., vol. 100, pp. 583–584, 2016, https://doi.org/10.1136/bjophthalmol-2016-308798.Search in Google Scholar PubMed
[8] N. Raoof, J. O’Hagan, N. Pawlowska, and F. Quhill, “’Toy’ laser macular burns in children: 12-month update,” Eye, vol. 30, pp. 492–496, 2016, https://doi.org/10.1038/eye.2015.222.Search in Google Scholar PubMed PubMed Central
[9] S. Androudi and E. Papageorgiou, “Macular hole from a laser pointer,” N. Engl. J. Med., vol. 378, p. 2420, 2018, https://doi.org/10.1056/nejmicm1714488.Search in Google Scholar
[10] J. E. Neffendorf, G. D. Hildebrand, and S. M. Downes, “Handheld laser devices and laser-induced retinopathy (LIR) in children: an overview of the literature,” Eye, vol. 33, pp. 1203–1214, 2019, https://doi.org/10.1038/s41433-019-0395-1.Search in Google Scholar PubMed PubMed Central
[11] E. Linton, A. Walkden, L. R. Steeples, et al., “Retinal burns from laser pointers: a risk in children with behavioural problems,” Eye, vol. 33, pp. 492–504, 2019, https://doi.org/10.1038/s41433-018-0276-z.Search in Google Scholar PubMed PubMed Central
[12] C. Vitellas, N. Doble, E. M. Wells-Gray, N. Challa, F. Davidorf, and S. Choi, “Cone photoreceptor integrity assessed with adaptive optics imaging after laser-pointer-induced retinal injury,” Retin. Cases Br. Rep., 2020, https://doi.org/10.1097/ICB.0000000000001025.10.1097/ICB.0000000000001025Search in Google Scholar PubMed
[13] J. M. Simonett, A. Shakoor, and P. S. Bernstein, “Intentional retinal injury with handheld lasers is an underrecognized form of self-harm,” J. Affect. Disord., vol. 281, pp. 503–504, 2021, https://doi.org/10.1016/j.jad.2020.12.065.Search in Google Scholar PubMed
[14] K. V. Bhavsar, Z. Michel, M. Greenwald, et al., “Retinal injury from handheld lasers: a review,” Surv. Ophthalmol., vol. 66, pp. 231–260, 2021, https://doi.org/10.1016/j.survophthal.2020.06.006.Search in Google Scholar PubMed
[15] T. A. Wheatley and W. Henderson, “Laser safety product compliance—who cares?” J. Laser Appl., vol. 31, 2019. Art no. 032007, https://doi.org/10.2351/1.5102067.Search in Google Scholar
[16] https://www.laserpointerpro.com/.Search in Google Scholar
[17] https://www.faa.gov/newsroom/dangerous-laser-strikes-reach-highest-numbers.Search in Google Scholar
[18] AS4970, Human Factor Considerations for Outdoor Laser Operations in the Navigable Airspace, Warrendale, Society of Automotive Engineers, Aerospace Standard (AS), 2011.Search in Google Scholar
[19] Advisory Circular 70-1B, Outdoor Laser Operations, Washington, Federal Aviation Administration, 2022.Search in Google Scholar
[20] ANSI Z136.1-2014, American National Standard for Safe Use of Lasers, Washington, American National Standards Institute, 2014.10.1364/FIO.2014.FW1F.2Search in Google Scholar
[21] IEC 60825-1:2014, Safety of Laser Products – Part 1: Equipment Classification and Requirements, Geneva, CENCENELEC Management Centre, 2014.Search in Google Scholar
[22] https://www.laserpointersafety.com/.Search in Google Scholar
[23] T. L. Lyon, “Hazard analysis technique for multiple wavelength lasers,” Health Phys., vol. 49, pp. 221–226, 1985, https://doi.org/10.1097/00004032-198508000-00002.Search in Google Scholar PubMed
[24] J. Mlynczak, K. Kopczynski, M. Kaliszewski, and M. Wlodarski, “Estimation of nominal ocular hazard distance and nominal ocular dazzle distance for multibeam laser radiation,” Appl. Opt., vol. 60, pp. 6414–6421, 2021, https://doi.org/10.1364/ao.431490.Search in Google Scholar PubMed
[25] L. Udovicic, Keeping an Eye on Safety – Protection Against Laser Radiation, Dortmund, Federal Institute for Occupational Safety and Health, 2013, ISBN 978-3-88261-733-7.Search in Google Scholar
[26] P. Lennie, J. Pokorny, and V. C. Smith, “Luminance,” J. Opt. Soc. Am. A, vol. 10, pp. 1283–1293, 1993, https://doi.org/10.1364/josaa.10.001283.Search in Google Scholar PubMed
[27] H. Cai and T. Chung, “Evaluating discomfort glare from non-uniform electric light sources,” Light. Res. Technol., vol. 45, pp. 267–294, 2012, https://doi.org/10.1177/1477153512453274.Search in Google Scholar
[28] CIE Report CIE 170-1:2006, Fundamental Chromaticity Diagram with Physiological Axes—Part 1, Vienna, International Commission on Illumination, 2006.Search in Google Scholar
[29] CVRL Database, CIE “physiologically relevan” luminous efficiency functions consistent with the Stockman & Sharpe cone fundamentals, 2-deg functions, London, UCL Institute of Ophthalmology. Available at: http://www.cvrl.org/.Search in Google Scholar
[30] http://www.nichia.co.jp/.Search in Google Scholar
[31] http://www.ushio-optosemi.com/.Search in Google Scholar
© 2022 Jaroslaw Mlynczak, published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Frontmatter
- Editorial
- Does journalism in B2B publishing work?
- Community
- Report: Laser World of Photonics 2022
- Letters
- Polarimetric 360° absolute rotary encoder
- Polarimetric linear absolute position encoder
- Research Articles
- Impacts of the gradient-index crystalline lens structure on its peripheral optical power profile
- Calculation and analysis of laser hazard distances in navigable airspace for multi-beam visible CW laser radiation
Articles in the same Issue
- Frontmatter
- Editorial
- Does journalism in B2B publishing work?
- Community
- Report: Laser World of Photonics 2022
- Letters
- Polarimetric 360° absolute rotary encoder
- Polarimetric linear absolute position encoder
- Research Articles
- Impacts of the gradient-index crystalline lens structure on its peripheral optical power profile
- Calculation and analysis of laser hazard distances in navigable airspace for multi-beam visible CW laser radiation

