Uncertainty Regarding Interpretation of the “Negligence Rule” and Its Implications for the Efficiency of Outcomes

Appendix

Lemma 1 Let <C, D, π, H, d^*> be an application belonging to 𝒜. Let c^*be such that (c^*, d^*)∈M. Then, regardless of the values of α and β, (c^*, d^*) is a Nash equilibrium.

Proof: Let <C, D, π, H, d^*>∈𝒜; and let (c^*, d^*)∈M.

EC1(c∗, d∗)=c∗+L(c∗, d∗)

c≠c∗→EC1(c, d∗)=c+L(c, d∗).

EC2(c∗, d∗)=d∗

d<d∗→EC2(c∗, d)=d+βL(c∗, d)+(1−β)[L(c∗, d)−L(c∗, d∗)] =d+L(c∗, d)−(1−β)L(c∗, d∗)

Therefore:

d>d∗→EC2(c∗, d)=d

(1.1)–(1.3) establish that (c^*, d^*) is a Nash equilibrium.□

Lemma 2 Let <C, D, π, H, d^*> be an application belonging to 𝒜; and let c^*be such that (c^*, d^*)∈M. If β≥α, then we must have:

(∀(c̅, d̅)∈C×D)[(c̅, d̅) is a Nash equilibrium →(c̅, d̅)∈M].

Proof: Let <C, D, π, H, d^*>∈𝒜. Let c^* be such that (c^*, d^*)∈M. Suppose (c̅, d̅) is a Nash equilibrium.

(c̅, d̅) is a Nash equilibrium implies

and

Now, if d̅<d^* we have:

EC1(c¯, d¯)=c¯+(1−α)L(c¯, d∗); EC2(c¯, d¯)=d¯+βL(c¯, d¯)+(1−β)[L(c¯, d¯)−L(c¯, d∗)]; EC1(c∗, d¯)=c∗+(1−α)L(c∗, d∗); and EC2(c¯,d∗)=d∗

Therefore if d̅<d^*, (2.3) reduces to:

If d̅≥d^* we have:

EC1(c¯, d¯)=c¯+L(c¯, d¯); EC2(c¯, d¯)=d¯; EC1(c∗, d¯)=c∗+L(c∗, d¯); andEC2(c¯, d∗)=d∗.

Therefore, if d̅≥d^*, (2.3) reduces to:

(2.4) and (2.5) establish that TSC(c̅, d̅)≤TSC(c^*, d^*). As total social costs are minimized at (c^*, d^*), it follows that TSC(c̅, d̅)=TSC(c^*, d^*); and consequently we must have (c̅, d̅)∈M. The proposition therefore stands established.□

Lemma 3 If 1>α>β>0, then there exists an application belonging to 𝒜 under which the efficiency does not obtain.

Proof: Let 1>α>β>0.

Choose positive numbers δ and θ.

Let 0<ϵ1<1−αα−βδ; 0<ϵ2<βα−βδ.

Let c0=1−αα−βδ+1−ααθ; d0=βα−βδ+ϵ2+λθ; where 0<β1−β1−αα<λ<1.^[4]

Now, consider the following application:

C={0, c₀}; D={0, d₀}. L(c, d), (c, d)∈C×D, is as given in the following array:

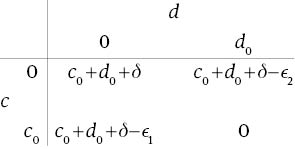
As ϵ₁<c₀ and ϵ₂<d₀, it follows that (c₀, d₀) is the unique TSC-minimizing care-configuration.

Let the due care for the injurer d^*=d₀.

We have:

(3.1) and (3.2) establish that (0, 0) is a Nash equilibrium. As (0, 0)∉M, it follows that efficiency does not obtain under the application considered here. This establishes the proposition.□

Lemma 4 If 1=α>β, then there exists an application belonging to 𝒜 under which the efficiency does not obtain.

Proof: Let 1=α>β.

Choose positive numbers δ, θ, ϵ₂ and c₀.

Let 0<ϵ₁<c₀ and d0=β1−β(c0+δ)+ϵ2+θ.

Now, consider the following application:

C={0, c₀}; D={0, d₀}. L(c, d), (c, d)∈C×D, is as given in the following array:

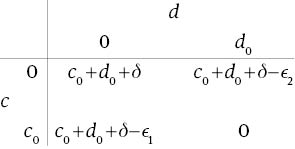
As ϵ₁<c₀ and ϵ₂<d₀, it follows that (c₀, d₀) is the unique TSC-minimizing care-configuration.

Let the due care for the injurer d^*=d₀.

We have:

(4.1) and (4.2) establish that (0, 0) is a Nash equilibrium. As (0, 0)∉M, it follows that efficiency does not obtain under the application considered here. This establishes the proposition.□

Lemma 5 If α>β=0, then there exists an application belonging to 𝒜 under which the efficiency does not obtain.

Proof: Let α>β=0.

Choose positive numbers δ, θ and d₀.

Let 0<ϵ₂<d₀

Let c0=1−αα(d0+δ)+θ; and let 0<ϵ₁<c₀.

Now, consider the following application:

C={0, c₀}; D={0, d₀}. L(c, d), (c, d)∈C×D, is as given in the following array:

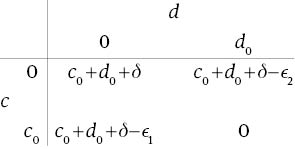
As ϵ₁<c₀ and ϵ₂<d₀, it follows that (c₀, d₀) is the unique TSC-minimizing care-configuration.

Let the due care for the injurer d^*=d₀.

We have:

(5.1) and (5.2) establish that (0, 0) is a Nash equilibrium. As (0, 0)∉M, it follows that efficiency does not obtain under the application considered here. This establishes the proposition.□

Theorem 1 A necessary and sufficient condition for efficiency under every application belonging to 𝒜 is that β be at least as large as α.

Proof: Let β≥α. Consider any a=<C, D, π, H, d^*> application belonging to 𝒜. (c^*, d^*) is a Nash equilibrium by Lemma 1. By Lemma 2 we have: (∀(c̅, d̅)∈C×D)[(c̅, d̅) is a Nash equilibrium →(c̅, d̅)∈M]. Therefore, it follows that the efficiency obtains under a. Next suppose that α>β. Then by Lemmas 3–5 there exists an application a=<C, D, π, H, d^*> under which the efficiency does not obtain. This establishes the theorem.□

Lemma 6 Let <C, D, π, H, d^*> be an application belonging to 𝒜_s. Then, if β>0 we must have:

(∀(c̅, d̅)∈C×D)[c̅, d̅) is a Nash equilibrium →(c̅, d̅)∈M].

Proof: Let β>0; and let <C, D, π, H, d^*>∈𝒜_s. Let c^* be such that (c^*, d^*)∈M. Suppose (c̅, d̅) is a Nash equilibrium.

(c̅, d̅) is a Nash equilibrium implies

and

If d̅<d^* we have:

EC1(c¯, d¯)=c¯+(1−α)L(c, d∗); EC2(c¯, d¯)=d¯+βL(c¯, d¯)+(1−β)[L(c¯, d¯)−L(c¯, d∗)]; EC1(c∗, d¯)=c∗+(1−α)L(c∗, d∗); and EC2(c¯, d∗)=d∗.

Suppose c̅<c^*∧d̅<d^*.

because the application under consideration belongs to 𝒜_s.

as TSC are minimized at (c^*, d^*).

From inequalities (6.4) and (6.5) we obtain: L(c̅, d̅)≥d^*–d̅+L(c̅, d^*),

which in turn implies that:

Now, EC2(c¯, d¯)=d¯+βL(c¯, d¯)+(1−β)[L(c¯, d¯)−L(c¯, d∗)]≥d¯+βL(c¯, d¯)+(1−β)[L(c∗, d¯)−L(c∗, d∗)], by (6.4)≥d¯+βL(c¯, d¯)+(1−β)[d∗−d¯], by (6.5)>d¯+β[d∗−d¯]+(1−β)[d∗−d¯], by (6.6) as β>0=d∗.

But by (6.2), EC₁(c̅, d̅)≤d^*.

This contradiction establishes that if c̅<c^*∧d̅<d^* then (c̅, d̅) cannot be a Nash equilibrium; and therefore:

If d̅≥d^* we have:

EC1(c¯, d¯)=c¯+L(c¯, d¯); EC2(c¯, d¯)=d¯; EC1(c∗, d¯)=c∗+L(c∗, d¯); andEC2(c¯, d∗)=d∗.

Therefore, if d̅≥d^*, (6.3) reduces to:

c¯+L(c¯, d¯)+d¯≤c∗+L(c∗, d¯)+d∗→c¯+d¯+L(c¯, d¯)≤c∗+d∗+L(c∗, d∗), as L(c∗, d¯)≤L(c∗,d∗), by (A2).

Next suppose d̅<d^*∧c̅≥c^*.

If d̅<d^*, (6.3) reduces to:

If c̅≥c^* then L(c̅, d^*)≤L(c^*, d^*) by (A2).

From (6.10), therefore, it follow that:

As total social costs are minimized at (c^*, d^*), it follows that: TSC(c̅, d̅)–TSC(c^*, d^*)≤0→TSC(c̅, d̅)=TSC(c^*, d^*); and consequently we obtain: TSC(c̅, d̅)–TSC(c^*, d^*)≤0→(c̅, d̅)∈M. (6.7), (6.8) and (6.11), therefore, establish the lemma.□

Lemma 7 If β=0∧α>0, then there exists an application belonging to 𝒜_sunder which the efficiency does not obtain.

Proof: Let β=0∧α>0.

Choose positive numbers δ and d₀.

Let c0>1−ααδ.

Now, consider the following application:

C={0, c₀}; D={0, d₀}. L(c, d),(c, d)∈C×D, is as given in the following array:

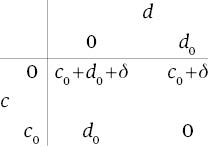
As δ>0 we obtain: M={(c₀, 0)(c₀, d₀)}.

Let the due care for the injurer d^*=d₀.

It is clear that this application belongs to 𝒜_s.

We have:

EC1(0, 0)=(1−α)(c0+δ); EC2(0, 0)=d0; EC1(c0, 0)=c0; and EC2(0, d0)=d0.

(7.1) and (7.2) establish that (0, 0) is a Nash equilibrium. As (0, 0)∉M, it follows that efficiency does not obtain under the application considered here. This establishes the proposition.□

Theorem 2 A necessary and sufficient condition for efficiency under every application belonging to 𝒜_sis that (β>0∨α=0).

Proof: If α=0 then regardless of the value of β we have: β≥α; therefore, by Theorem 1, efficiency obtains under every application belonging to 𝒜_s, as 𝒜_s⊂𝒜. Let β>0. Consider any a=<C, D, π, H, d^*> belonging to 𝒜_s. (c^*, d^*) is a Nash equilibrium by Lemma 1 as 𝒜_s⊂𝒜. By Lemma 6 we have: (∀(c̅, d̅)∈C×D)[(c̅, d̅) is a Nash equilibrium →(c̅, d̅)∈M]. Therefore, it follows that the efficiency obtains under a. This establishes the sufficiency part of the theorem. If (β=0∧α>0) then by Lemma 7 there exists an application belonging to 𝒜_s under which efficiency does not obtain; which establishes the necessity part.□

Lemma 8 Let a=<C, D, π, H, d^*> be an application belonging to 𝒜_s∩𝒜_m. Then:

(∀(c̅, d̅)∈C×D)[(c̅, d̅) is a Nash equilibrium →(c̅, d̅)∈M].

Proof: Let a=<C, D, π, H, d^*>∈𝒜_s∩𝒜_m. Let c^* be such that (c^*, d^*)∈M. Suppose (c̅, d̅) is a Nash equilibrium.

(c̅, d̅) is a Nash Equilibrium implies

and

If d̅<d^* we have:

EC1(c¯, d¯)=c¯+(1−α)L(c¯, d∗); EC2(c¯, d¯)=d¯+βL(c¯, d¯)+(1−β)[L(c¯, d¯)−L(c¯, d∗)]; EC1(c∗, d¯)=c∗+(1−α)L(c∗, d∗); and EC2(c¯, d∗)=d∗.

Suppose c̅<c^*∧d̅<d^*.

as TSC are uniquely minimized at (c^*,d^*) because a∈𝒜_m.

Now, EC₂(c̅, d̅)=d̅+βL(c̅, d̅)+(1–β)[L(c̅, d̅)–L(c̅, d^*)]

>d̅+(d^*–d̅), by (8.7)

=d^*.

But by (8.2), EC₂(c̅, d̅)≤d^*.

This contradiction establishes that if c̅<c^*∧d̅<d^* then (c̅, d̅) cannot be a Nash equilibrium; and therefore:

If d̅≥d^* we have:

EC₁(c̅, d̅)=c̅+L(c̅, d̅); EC₂(c̅, d̅)=d̅; EC₁(c^*, d̅)=c^*+L(c^*, d̅); and

EC₂(c̅, d^*)=d^*.

Therefore, if d̅≥d^*, (8.3) reduces to:

c¯+L(c¯, d¯)+d¯≤c∗+L(c∗, d¯)+d∗→c¯+d¯+L(c¯, d¯)≤c∗+d∗+L(c∗, d∗), as L(c∗, d¯)≤L(c∗, d∗), by (A2).

Next suppose d̅<d^*∧c̅≥c^*.

If d̅<d^*, (8.3) reduces to:

If c̅≥c^* then L(c̅, d^*)≤(c^*, d^*) by (A2).

From (8.11), therefore, it follow that:

(8.12)d¯<d∗∧c¯≥c∗→TSC(c¯, d¯)−TSC(c∗, d∗)≤0. (8.12)

As total social costs are minimized at (c^*, d^*), it follows that: TSC(c̅, d̅)–TSC(c^*, d^*)≤0→TSC(c̅, d̅)=TSC(c^*, d^*); and consequently we obtain: TSC(c̅, d̅)–TSC(c^*, d^*)≤0→(c̅, d̅)∈M. (8.8), (8.9) and (8.12), therefore, establish the lemma.□

Theorem 3 Efficiency obtains under every application belonging to 𝒜_s∩𝒜_m.

Proof: Consider any application a=<C, D, π, H, d^*> belonging to 𝒜_s∩𝒜_m. (c^*, d^*) is a Nash equilibrium by Lemma 1 as 𝒜_s∩𝒜_m⊂𝒜. By Lemma 8 we have: (∀(c̅, d̅)∈C×D)[(c̅, d̅) is a Nash equilibrium →(c̅, d̅)∈M]. Therefore, it follows that efficiency obtains under a. This establishes the theorem.□