Abstract
This article seeks to explain the outbreak of war between Ukraine and Russia in February 2022. The cause of the conflict appears to be very simple: Vladimir Putin wanted to go to war with Kyiv. However, as the bargaining model of war states: a conflict takes at least two actors, both of whom are determined to stop negotiating and resort to arms. We argue here that the negative spiral which led to the outbreak of war can be explained as the outcome of three interrelated strategic games that produced a failure in the US/NATO deterrence posture towards Moscow, an unclear (emboldening?) message sent by the US/NATO to Ukraine, and a misunderstanding of Russia’s war aims (limited vs. unlimited) in Ukraine. A formal model is proposed that explains the outcome of the crisis as the equilibria produced by the interaction of the three actors’ decisions.
“When a state wishes to deter an opponent and also restrain an ally from provoking an opponent, the two goals may work against each other. Deterrence requires a firm stance, which may indirectly encourage the ally to excessive belligerence; restraint of the ally may mean threatening to withhold support, but that may undermine deterrence if the adversary ‘overhears’ the threat.”
G.H. Snyder (1997: 329)
1 Introduction
The Russian invasion of Ukraine caught everyone by surprise. American and British intelligence services warned of the risk of an invasion in the fall of 2021, but the warning was underestimated by their European colleagues – and by analysts and scholars in general – who, for the most part, were convinced that President Putin’s strategy was solely to force Ukraine into accepting the loss of Crimea and the annexation of the Donbas region without waging a large-scale war. In line with this interpretation, an article published on 15 February 2022 in The New York Times explained that troop movements, threats and counter-threats were part of a “resolve war” that Russia and America were playing to avoid a real war.[1] With hindsight, this analysis was wrong. The actors’ intentions were either misread, or something happened in the nine days between the publication of the article and the outbreak of war that changed the actors’ preferences.
The cause of the conflict appears to be very simple: Moscow wanted to go to war with Kyiv.[2] However, as the bargaining model of war maintains, a conflict takes at least two actors, and wars only break out when both of them think that continuing to negotiate is useless and it will be better off fighting than not fighting (Fearon 1995; Powell 2002).[3] In the case of the Ukrainian crisis, we therefore have to explain: (1) why Russia was convinced that it could fight a war against Ukraine in which US/NATO support would be only lukewarm,[4] and a blitzkrieg would be possible;[5] (2) why the US/NATO was unsuccessful in delivering a message of resolve to Russia; (3) and how Ukraine interpreted the ambivalent message communicated by the US/NATO.
We argue here that the negative spiral which produced the outbreak of the war can be explained by playing a strategic game in which the three players make simultaneous decisions. Peculiar to this game is the failure of the US/NATO deterrence posture towards Russia, the uncertain support of Ukraine by the US/NATO and the misunderstanding of Russia’s real aims regarding Ukraine.
To provide an explanation of the outbreak of war based on the rational moves of the three players, we first determine the possible decisions of each player and then calculate their consequences. The 2014 Crimea invasion was the outcome of a game – consistent with an equilibrium in pure strategies – in which Russia invades, the US/NATO does not support, and Ukraine concedes. As will be seen, this result is consistent with the negotiated outcome of the bargaining model of war (Fearon 1995).
Western analysts and policymakers expected the 2022 crisis to be a continuation of the same game. Unfortunately, by that time, the Russian payoff structure had changed. More than a mere territorial dispute, the conflict with Ukraine sought to establish an administration subservient to Moscow and to prevent any attempt by the other former Soviet republics to move closer to the West. This change had a dramatic effect on the game. For Ukraine, to fight was a matter of survival. As a result, the three-player game, instead of reducing to a version of the bargaining model, turns into a Sanction game played by Russia and NATO. The Sanction game is a model proposed by George Tsebelis to explain the difficult implementation of effective sanctions on rogue states (Tsebelis 1990, 1993). In the Sanction game, a state can decide not to comply with some international agreement: in our application, Russia invades. Then, a second power can decide to impose sanctions: here, the US/NATO supports the Ukrainian military effort. The Sanction game is characterised by only one equilibrium in mixed strategies; that is, the outcome of the model is not deterministic, but results from players’ probability assessments.
Here, we found again one of the causes of conflicts for the bargaining model, that is, asymmetric information and chance and risk-proneness, an issue well discussed in Idrisoglu and Spaniel (2024). However, we have framed war as a three-player game, and therefore we have to ascertain the role of the Western alliance in the conflict, something that is less apparent when considering only two players in the bargaining game: Russia and Ukraine.
Our argument is structured as follows. In Section Two, we identify the decisions available to the three players: Russia, Ukraine and US/NATO. In an abstract setting, a state of the world, or an outcome, results as the consequence of their three decisions. We infer what the (conflicting) preferences of the players are on these outcomes, to form rankings that are the basis of their actual choices. As can be seen, we state that the players’ preference rankings have changed from 2014 to 2022, and this has had a profound impact on the model’s predictions, as explained in the first subsection of Section Three. Framing decisions and preferences as a three-player game, we calculate the Nash equilibria to predict and interpret the course of actions that preceded the war.
After comparing the games of 2014 and 2022, we claim that two main factors contributed to the conflict: Russia’s desire to reassert the former Soviet Union borders, and the lukewarm interest of the US/NATO in protecting Ukraine. We say “contributed to” instead of “triggered” because, as our game-theoretic analysis demonstrates, the game played in 2022 differed greatly from the one in 2014. The 2022 three-player game can be reduced to a two-player game between the US/NATO and Russia, whose structure is the same as the Sanction game, with players randomly choosing between peace and war.[6] According to this interpretation, war was not the outcome of a deterministic course of action, but rather the result of hazardous decisions that took into account the probability of escalation.[7]
In subsection 3.2, we compare our three-player game with the bargaining model, as recently applied to the Ukrainian war (Wolford 2024). We put forward that the issue of indivisibility is one of the causes that are consistent with that model. However, while Fearon’s model does not provide any insight about how a war can continue, here we can see the consequences of the involvement of the third player.
In subsection 3.3, we try to advance an interpretation of the actual meaning of the mixed strategies in international disputes. We introduce incomplete information to the game. We assume that the US/NATO is not fully aware of the Russian cost of conflict, and Russia is not fully aware of the US/NATO reputational cost of leaving Ukraine defenceless. This leads us to explain the war as a consequence of Russia’s underestimation of the probability of US/NATO intervention. Indeed, the mixed strategy equilibrium can be understood as the long-term behaviour of a game in which players are uncertain of the opponent’s payoff, and, therefore, they make decisions in a riskier environment. Note that this is consistent with Fearon’s prediction of war for private information in the form of probability assessments. The conclusions summarise the empirical evidence and the strengths and weaknesses of our analysis.[8]
2 A Formal Analysis of the Players’ Preferences
The first aspect to consider in analysing the Russia-Ukraine conflict is its strategic context (CRS 2022). This is characterised by the increasing rivalry between Russia and America, triggered by the former’s desire to regain a place of primacy in international politics and reaffirm its regional hegemony in the post-Soviet space,[9] and the latter’s intention to expand its security barriers. To derail Washington’s goal, Moscow tried to signal its displeasure both with words and deeds. The imbalance of interests at stake convinced observers that the US/NATO would never go to war with Russia over Ukraine.
The US/NATO was in the uncomfortable position of having to protect a state from an attack while avoiding any offer of unconditional support that can elicit a moral hazard effect, in which a protégé acts more recklessly, thereby increasing the risk of the defender being dragged into an unwanted war (Snyder 1984, 1997; Benson et al. 2014). The fact that Moscow was well aware of this “alliance dilemma” compromised the credibility of the US/NATO’s deterrence posture.[10] Trapped in a three-person game, the US/NATO acted towards Ukraine taking into account Kyiv’s potential moves towards Russia, Ukraine made its decisions about Russia after discounting America’s moves, and Russia behaved towards Ukraine after calculating the US/NATO’s level of commitment.
In the winter of 2021–2022, international observers thought that Moscow’s preferences in this regional dispute were (in decreasing order): to maintain the status quo, i.e. to “freeze” its de facto control of the eastern part of Ukraine; to strengthen its control of Donbas and/or annex more territory in a limited conflict (as in Crimea in 2014); and, only as a last resort, to fight a large-scale war against Ukraine.[11] Unfortunately, this ranking proved to be wrong, and the hardening of Russian demands before the crisis signalled a shift in preferences from limited to unlimited war aims. Limited war aims assume that the aggressor has restricted goals that exclude the enemy’s capitulation. This leaves the state under threat with two choices. It can back down without fighting or agree to fight. To back down is realistic because it does not risk the annihilation of the attacked state. This is consistent with what occurred in the 2014 Crimean crisis, where Russia attacked and Ukraine backed down but remained independent.
In the 2022 crisis, intelligence warned that Russia had revised its aims and President Putin was preparing an invasion in three directions: from the east towards Donbas, from the south towards Mariupol, and the north, straight to Kyiv. The American Institute for the Study of War, which monitored the situation on the ground daily, warned that the main axis of advance was in the north, towards the Ukrainian capital, while the other two were only to sustain the main effort and therefore of secondary importance.[12] Force deployment confirmed that the scope of the Russian operation was unlimited and aimed to mount a blitzkrieg to disrupt the enemy’s political-military command centres.
When war aims are unlimited, the stronger actor A not only prefers coercion to compromise but, for several reasons, prefers that actor B refuses to compromise, so it “can” wage a war to destroy the enemy. From a historical perspective, Russia’s war against Ukraine is reminiscent of Austro-Hungary’s actions against Serbia before World War I, or Germany’s actions against the Czech Republic in 1938.[13] President Putin needed a conflict with Ukraine to teach all post-Soviet states a lesson, avoid the risk of democratic contagion in the post-Soviet republic, and halt the potential eastern expansion of NATO.[14] These objectives went far beyond the annexation of Crimea and the eastern region of Donbas, and in the face of such a lethal threat to its survival, the Ukrainian leadership could do nothing but escalate the conflict and fight.
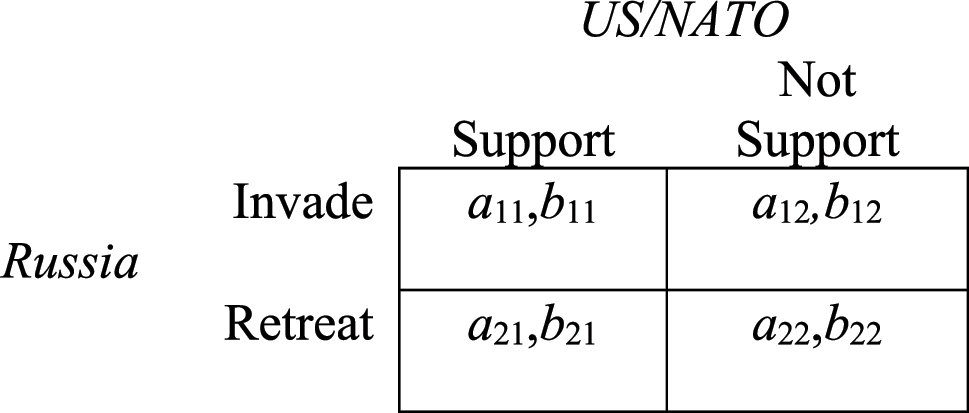
The main options available to players and their outcomes are summarised in Table 1. Combining all three players’ decisions, different outcomes to a large-scale war could have occurred, but they were not plausible from a game-theoretic point of view. To explain the outcome, we therefore need to rank the players’ preferred outcomes from A to H and explain their choices.
Decisional alternatives in a three-player game.
| US/NATO (towards Ukraine) | Ukraine (towards Russia) | Russia (towards Ukraine) | Outcome |
|---|---|---|---|
| Support | Concede | Concede | A: Supported compromise |
| Not support | Concede | Concede | B: Unsupported compromise |
| Support | Concede | Stand firm | C: Ukraine supported withdrawal |
| Not support | Concede | Stand firm | D: Ukraine unsupported withdrawal |
| Support | Stand firm | Concede | E: Russian retreat with Western enlargement |
| Not support | Stand firm | Concede | F: Russian retreat without Western enlargement |
| Support | Stand firm | Stand firm | G: Large-scale war |
| Not support | Stand firm | Stand firm | H: Localised war |
The US/NATO decisions can be summarised as to Support or Not Support Ukraine. This is an oversimplification of all the options that could have shaped the US/NATO relations with the Ukrainian government. However, the bulk of an alliance is to provide or not to provide military support, and we can assume that this binary decision covers all forms of alliance. As we will see later, the mixed-strategies equilibria can be interpreted as the level of commitment to the alliance, with values ranging from no aid to full military support. The US/NATO’s policy towards Ukraine, because of the “alliance dilemma”, was characterised by a less than clear attitude. The US/NATO tried to reassure Kyiv without antagonising Moscow, which was, as John Mearsheimer claims, an impossible mission.[15]
In 2014, when Moscow seized Crimea, America’s reaction was soft. Notwithstanding the rhetoric of expanding NATO (and the European Union) to the east, the Atlantic Alliance never began a genuine discussion about the membership of Ukraine. US/NATO policymakers were worried that they were intruding into Russia’s backyard and that this could trigger a conflict escalation between the East and West. On the eve of the Crimea takeover, both NATO’s secretary, Anders Rasmussen, and the US President, Barack Obama, warned that Russia’s military intervention would not be accepted. Nevertheless, after the fact, Obama only threatened Russia with generic costs in retaliation for its actions and announced that the US would suspend its participation in the preparatory meetings of the G8 in Sochi. As reported in an article in The Guardian on 26 March 2014:
It was clear Obama had no intention of being drawn into rash action or any kind of dangerous confrontation with Putin over Ukraine. “This is not another Cold War that we’re entering into. The United States and NATO do not seek any conflict with Russia,” Obama said. “Now is not the time for bluster […] There are no easy answers, no military solution”.[16]
Some years later, members of the Republican Party and President Donald Trump attacked the former administration for having been too soft towards Russia at the time of the Crimean annexation:
Obama’s response to Russia’s invasion of Crimea in March 2014, and Moscow’s subsequent support of pro-Russian rebels in eastern Ukraine was economic sanctions. Although the measures had an impact on the Russian economy, they were seen as woefully inadequate by some Republican lawmakers in Congress. Senator John McCain of Arizona, a harsh critic of Obama’s foreign policy, wanted the US to send arms to Ukraine. But Obama viewed the Ukraine conflict through another lens […] “Obama’s theory here is simple: Ukraine is a core Russian interest but not an American one, so Russia will always be able to maintain escalatory dominance there.”[17]
Despite Trump’s rhetoric, his policy towards Ukraine/Russia and his affinity with the Russian leader made his position even more ambivalent than Obama’s. During the presidential campaign, and compared to his presidential predecessors, Joe Biden had a tougher attitude towards the Ukraine crisis. Once elected, he began a more assertive policy, but he never reached the point of considering Kyiv a potential NATO member.[18]
From these basic premises and also considering the vulnerability of Western European NATO members to Russian energy blackmail,[19] it follows that the best outcome for the US/NATO in 2022 was a compromise between Ukraine and Russia without any heavy direct military commitment. This is indicated in Table 1 as B = Unsupported Compromise. Conversely, given the magnitude of Russian military operations, the worst outcome would be a local war between Ukraine and Russia, which is indicated as H = Localised War. Without external support, a localised war would entail the total capitulation of Ukraine and a resounding victory for Russia. Allowing Russia to annex Ukraine would have been seen as a sign of weakness. So, in this course of events, the US/NATO preferred to be involved in a conflict, outcome G, rather than seeing the defeat of Ukraine. This justifies G > H in the ranking 1(a). Considering all the intermediate outcomes presented in Table 1, we hypothesise that the US/NATO ranked preferences in February 2022 were:[20]
This contrasts with the preferences that characterised the Crimean crisis in 2014, where the Russian goal appeared more limited. In that context, a localised war entailed the annexation of Crimea, a disturbing consequence but certainly not worthy of a large-scale conflict. So, preferences in 2014 are similar to 1(a), but with the position of H and G reversed:
Observed Russian decisions seemed to point clearly to Stand firm and take the risk of incurring a conflict. However, the question is whether Russia was pursuing limited or unlimited war aims, that is to say, did it intend to simply occupy more Donbas territory or implement a full invasion. The post-Soviet space has a special role in Russia’s foreign policy. When a dispute is about a territory located in the former Soviet Union countries, the probability of military escalation increases dramatically (Rosa and Cuppuleri 2021). These territories have a high score on Paul Hensel’s scale of issue salience (Hensel et al. 2008). Ukraine, in particular, scores high on all six indicators:
Territory is considered a homeland territory;
Territory is inhabited by a permanent population;
Territory previously belonged to the claimant state;
Territory may contain important natural resources;
Territory has an important economic or strategic position;
Groups living on the territory have some sort of ethnic/cultural relationship with the claimant state.
These elements make the post-Soviet space a critical “bone of contention” the Kremlin is ready to use military force for. As Mearsheimer puts it, a great power doesn’t tolerate the interference of external actors in its backyard. On the day of the invasion, President Vladimir Putin stated on Russian television the main aims of the attack on Ukraine:
It is a fact that over the past 30 years we have been patiently trying to come to an agreement with the leading NATO countries regarding the principles of equal and indivisible security in Europe. In response to our proposals, we invariably faced either cynical deception and lies, or attempts at pressure and blackmail, while the North Atlantic alliance continued to expand despite our protests and concerns.
For our country, it is a matter of life and death, a matter of our historical future as a nation. […] It is not only a very real threat to our interests but to the very existence of our state and to its sovereignty. It is the red line which we have spoken about on numerous occasions. They have crossed it.[21]
From Russia’s perception of its regional role and the alleged existential threat posed by the US/NATO to its national security, we can infer that Russia’s ranked preferences would put a localised war against Ukraine without US/NATO involvement first, indicated as H = Localised war; and a war against Ukraine backed by the US/NATO as the least preferred outcome, indicated as G = Large-scale war. H was even preferred to the unilateral surrender of a non-belligerent Ukraine (outcome D), as the scope of the invasion was not only military annexation but also to send a signal to the other post-Soviet republics about Russian resolve. Considering all the alternatives in between, the ranked preferences for Russia in 2022 were therefore:
This differs from the preferences that characterised the Crimean crisis of 2014, when Russia’s aim was the occupation of an area that had traditionally been part of the homeland since the days of Tsarist Russia.[22] So, Moscow’s preferences in 2014 are similar to 2(a), but with the position of D and H reversed:
Ukraine’s decisions can be summarised as Concede or Stand firm. However, ranking its preferences is more complicated because they are highly dependent on the perception of the level of US/NATO commitment. The higher the expectation of a strong commitment, the more likely Ukraine would be to Stand firm, with a subsequent increase in the risk of an inadvertent large-scale conflict. Between late 2019 and spring 2020, there was a spike in ceasefire violations, and the first Russian military escalation along the border was observed. It is probably at this time that the Ukrainian president began to seek NATO support. Elected as a low-profile candidate and possible peacemaker, up until then Volodymyr Zelensky had not explicitly stated his “Atlanticist” aspirations. The Washington plan of offering Ukraine an extraordinary package of defensive military assistance also dates back to that period (ISW 2019). Despite this, the perspectives of European Union (EU) or NATO membership were never viable options. At the 23rd meeting between the EU and Ukraine held on 12 October 2021, the final declaration was very vague about the future strengthening of the association agreement.[23] European Commission representatives assessed the bilateral cooperation between the two entities as positive, but remarked that the EU was not ready to take further steps on advancing the Ukrainian European Perspective.[24] As the crisis deepened, Kyiv sought a stronger commitment from the US/NATO. However, the level of political/military support that Ukraine might receive was uncertain. Zelensky clearly realised this:
NATO offered Ukraine a path towards membership in 2008. After Russia’s annexation of Crimea in 2014, Ukraine made joining a priority. But this has not happened, mainly because of Russia’s long-standing opposition. One of Russia’s demands before the invasion was that Ukraine should never be allowed to join – something NATO refused to accept. Russia believes NATO has been encroaching on its area of political influence by taking on new members from eastern Europe, and that admitting Ukraine would bring NATO right into its backyard.
Ukraine’s President Zelensky has accepted that his country can’t join NATO at present, saying: “It is clear that Ukraine is not a member of NATO. We understand this”.[25]
Biden’s administration repeatedly excluded NATO membership up until January 2022. Finally, given the impossibility of a formal alliance, Zelensky tried to secure a steady supply of weapons. These began to be delivered in the fall of 2021, and the quantities supplied quickly increased as the crisis escalated.[26]
Taking all this into consideration, as well as the threat to its sovereignty posed by Russia, the priority of the Ukrainian leadership was to avoid its country’s disintegration by standing firm against Russian encroachment, preferably with a strong commitment from the US/NATO (E = Russian retreat with Western enlargement). The intermediate options were a compromise and waging war against Russia with (or without) external military support (G = Large-scale war > H = Localised war). A total surrender (C and D) was the least preferred option. Thus, Ukraine’s ranked preferences in February 2022 were:
This ranking contrasts with the ranking on the eve of the 2014 Crimean crisis. The difference is that in 2022, conceding (options C and D) was the worst-case scenario, as it would imply the country’s annihilation.[27] Outcomes G and H – local or large-scale war – were preferred to C and D because at least there was a chance of Ukraine surviving as an independent state. Conversely, making concessions was still a convenient strategy in 2014, as the loss of territories was not a threat to the country’s survival. We can therefore argue that in 2014, C and D were preferable to G and H:[28]
3 A Game-Theoretic Model of the Ukrainian Crisis
3.1 The Alliance Dilemma as a Three-Player Game
In the following section, the interactions between the players’ preferences are structured as a game, and their equilibria are calculated to interpret the different outcomes in 2014 and 2022. To simplify our discussion, we have replaced the 1(a) to 3(b) order with ordinal utility functions. More formally, as there are eight ranked outcomes, we have assigned a score of 8 to the most preferred outcome and 1 to the least preferred outcome.
The situation in 2014 is shown in Figure 1. Figure 1(a) indicates the normal-form game between Russia and Ukraine in a scenario in which the US/NATO does not support Ukraine. Figure 1(b) shows a scenario in which the US/NATO supports Ukraine against Russia. The case represented by Figure 1(a) shows that for Russia, Stand Firm is the dominant strategy, as the payoffs [8, 7] are greater than the payoffs [5, 3] resulting from the Concede strategy. Without any support from the US/NATO, Ukraine can only back down in the face of Russian claims and accept concessions. So, in Figure 1(a), when the game is played in the “US/NATO doesn’t support” scenario, the equilibrium is: Ukraine concedes and Russia stands firm. Figure 1(b) indicates the scenario in which the US/NATO supports Ukraine against Russia. This game is characterised by two equilibria: Concede/Stand firm, and Stand firm/Concede, a version of the Hawk and Dove game. The peaceful situation (both choose Concede) is threatened by the aggressive stance of the players, which is profitable as long as the opponent remains remissive. If both players are aggressive (both choose Stand firm), their results are the worst.
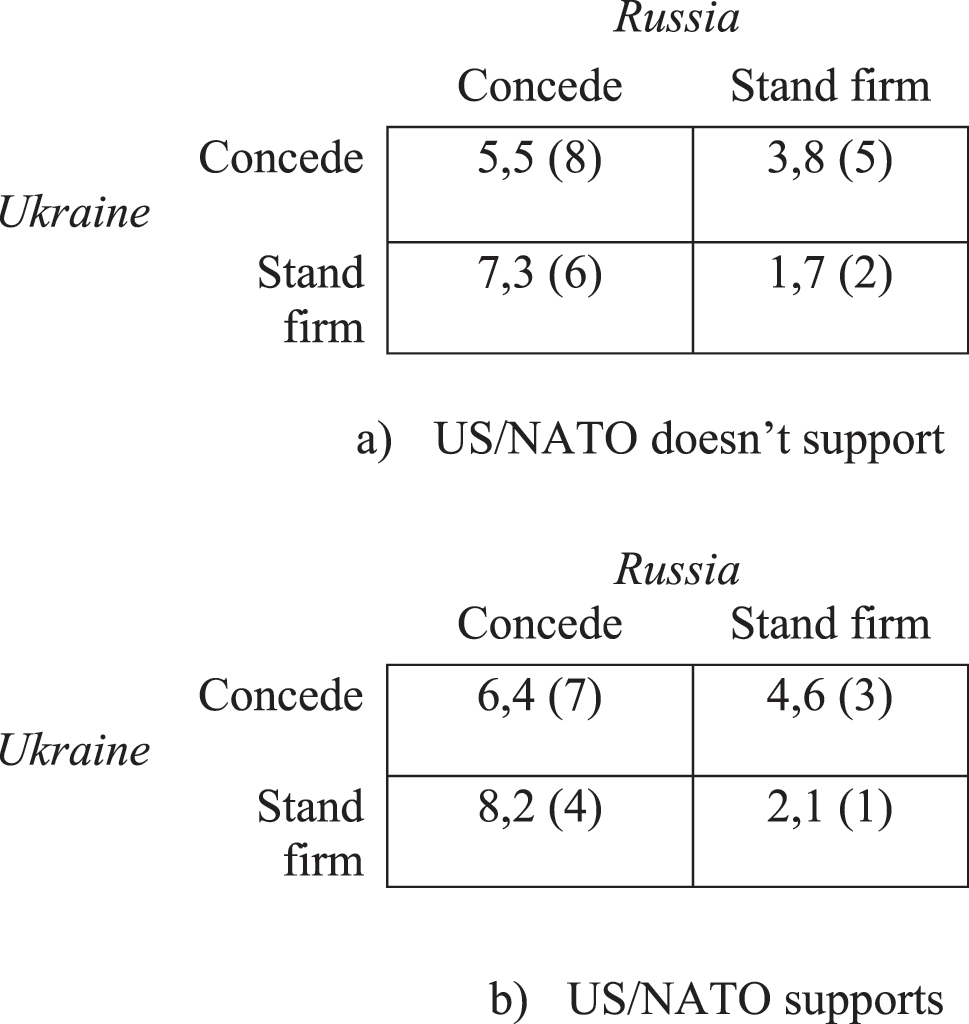
Russia-Ukraine crisis, 2014. Legenda: The figures in parentheses represent US/NATO ranked preferences.
The equilibria in Figure 1(a) and (b) depend on US/NATO preferences. If we compare the two scenarios, we can see that “Not support Ukraine” is the dominant US/NATO strategy, as the outcomes [8, 5] and [6, 2], determined by the preferences in parentheses in Figure 1(a), are respectively greater than the outcomes [7, 3] and [4, 1], determined by the preferences in parentheses in Figure 1(b). So, in the game between Russia and Ukraine played in Figure 1(a), Russia stays firm, and Ukraine yields. A result that is consistent with the annexation of Crimea.
The situation in 2022 is reported in Figure 2. Figure 2(a) shows the normal-form game between Russia and Ukraine in a scenario in which the US/NATO does not support Ukraine, and Figure 2(b) in a scenario in which the US/NATO supports Ukraine.
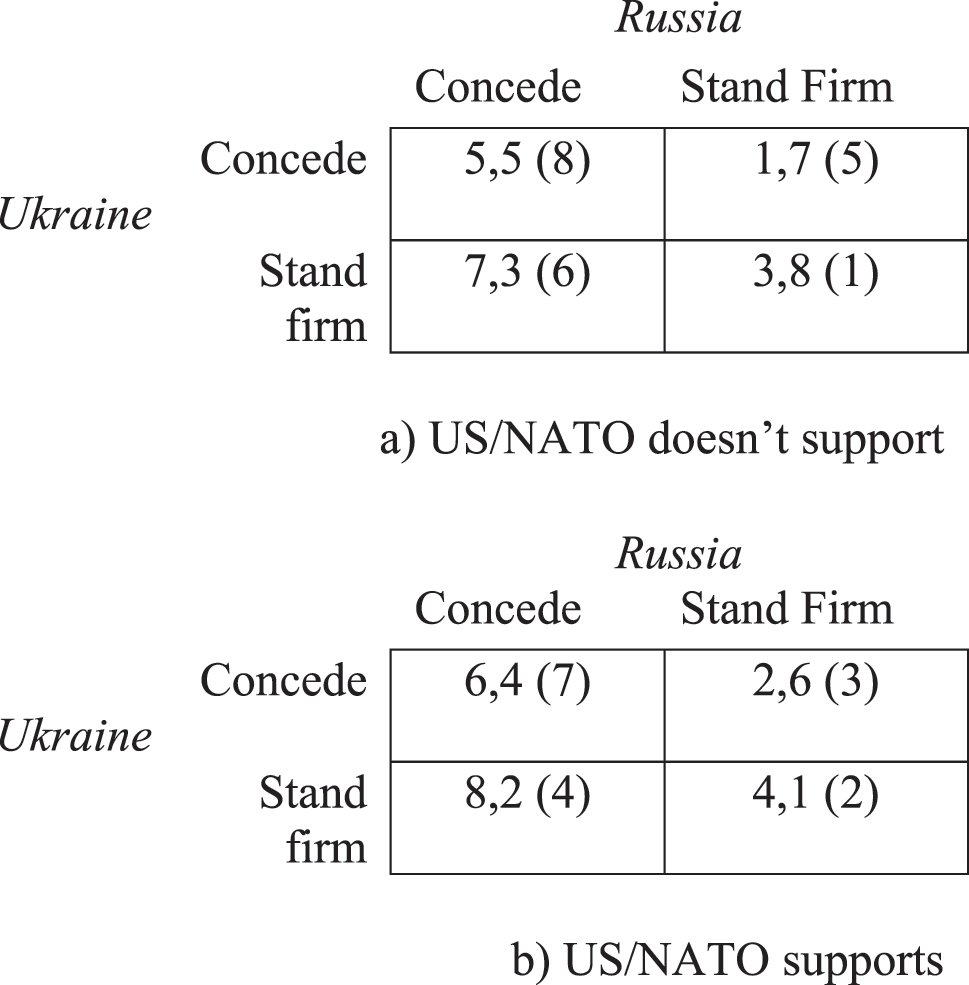
Russia-Ukraine crisis, 2022. Legenda: the figures in parentheses represent US/NATO ranked preferences.
Compared to the situation in 2014, the Not Support strategy is no longer a dominant strategy for the US/NATO. In the event of escalation, the US/NATO prefers to intervene. In Figure 2(a) we can see that without US/NATO support, Russia’s dominant strategy is to stay firm, as in 2014. But now, Ukraine’s best response is to stay firm as well, and therefore, when the game is played in Figure 2(a), the outcome is both nations staying firm, which corresponds to the outbreak of war. In case of war, the US/NATO prefers to intervene, leading the game on to the 2(b) model. In this game, Stand Firm is Ukraine’s dominant strategy, as the outcomes [8, 4] are better than [6, 2] and given this strategy, Russia’s best reply should be to concede. However, the 2022 game does not admit an equilibrium in pure strategies, as in every cell of the game in Figure 2, at least one player can deviate from their move. More formally, in Figure 2(b) when the game is restricted to Ukraine and Russia, the only potential equilibrium is “Stand firm, Concede”. But that outcome is not an equilibrium because in that case the US/NATO would prefer to defect, involving a shift to game 2(a).
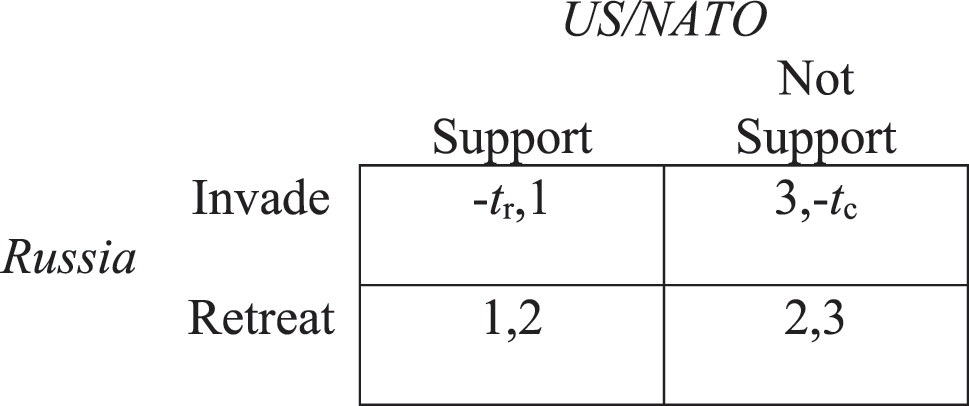
Nonetheless, there is an equilibrium in mixed strategies that can be calculated as follows. In 2022, Stand Firm is the dominant strategy for Ukraine, as the outcomes [8, 4, 7, 3] are greater than [6, 2, 5, 1]. We can, therefore, restrict the analysis to the game between Russia and the US/NATO. This game is reminiscent of Frank Zagare’s Challenger-Defender subgame (Zagare 2019), and it is shown in Figure 3.

The Russia-US/NATO subgame, 2022.
This shows that there is no pure-strategies equilibrium. Starting from the status quo before the invasion (the US/NATO does not support, and Russia concedes), Russia realises that its best outcome is to stand firm and invade, to which the US/NATO replies by supporting Ukraine. The game moves from payoffs (3, 6) to payoffs (8, 1), and payoffs (1, 2). Here, Russia suffers its worst outcome and seeks concessions by moving to (2, 4). At this point, the US/NATO has an incentive to move to (3, 6), to return to the former status quo. However, the game has an equilibrium in mixed strategies. If we focus on Russian decisions, Standing firm means invasion, so we indicate the probability that Russia stands firm as p[Invasion]. A straightforward calculation provides the equilibrium strategy p[Invasion] = 2/3. Let q[Support] be the probability that the US/NATO reacts, then the equilibrium strategy is q[Support] = 5/6. However, these numbers should not be taken literally. We compiled Figure 3 with the simplest numbers, reflecting the ordered preferences as described in 1(a)-3(b), and, if we were to use them to calculate a mixed strategy, then we should be able to express them as a cardinal number, i.e. to measure to what degree an outcome is preferable to another.
The game’s structure is summarised in parametric form in Figure 4. The parameters satisfy the conditions: a 11 < a 21 and a 12 > a 22 for Russia and b 11 > b 12 and b 21 < b 22 for the US/NATO. Given these conditions, no pure strategy equilibria exist for these games, and the only equilibrium is in mixed strategies (Tsebelis 1990). Formally, the optimal strategy for Russia is to play Invasion with the probability:
and the optimal strategy for the US/NATO is to play Support with the probability
The Russia-US/NATO subgame, 2022, in its parametric form.
The existence of only one equilibrium in mixed strategies highlights the strategic uncertainty before war onset. Given the Kremlin’s determination to get rid of the Ukrainian government, for Kyiv it was a matter of survival to stand firm, enter the war in any case, and hope that they would obtain Western support. Conversely, Russia and the US/NATO found themselves in a dilemma. They had to try to ascertain their opponent’s costs and benefits, that is to say, to predict whether Russia would retreat or the US/NATO would support.
If predictions of opponents’ behaviour are taken into account, all outcomes become plausible, to the point that only a probabilistic deduction can be used for this game. In other words, the structure of the strategic game shows that states do not make decisions in a deterministic framework, i.e. a context in which every decision corresponds to an optimal best reply. Instead, they operate in a probabilistic environment in which a degree of randomness inevitably characterises their choices. In the case of the game shown in Figure 4, no player can conveniently (and credibly) announce a strategy without their opponent turning the consequences to their advantage, which triggers a chain reaction.
So, the main lesson of the Russia-US/NATO game is that the outcome was unpredictable. Due to the non-existence of a pure-strategies equilibrium, given the parameters, only the probabilities p[Invasion] and q[Support] could be calculated. The resulting game is deduced by the preference orderings stated in the previous section, and the actual probabilities of war depend on the parameters of Figure 4. If orderings were to be changed, different games would be more appropriate to model the conflict.
3.2 The Alliance Dilemma and the Bargaining Model of War
In the previous section, we discussed the differences between the conflicts of 2014 and 2022. The outcome of 2014 was Crimea’s annexation, which stalled as a frozen conflict between the two states. Conversely, in 2022, a full-fledged conflict broke out. We interpreted those occurrences as the consistent outcomes of a three-player game, in which the role of the third player, the US/NATO, is central to explaining the course of the events. Political scientists have often interpreted wars through Fearon’s bargaining model, and Ukraine’s war is not an exception (Wolford 2024). According to the model, war is a bargaining failure, because the same agreement that terminates the war could have been agreed on before the war, avoiding the cost of the conflict. Therefore, any rationalist war explanation must provide at least a hint about why bargaining had failed. In what follows, we will see how our results on the alliance dilemma are consistent with the bargaining model. Moreover, the inclusion of a third player provides new insights into the case.
Fearon’s model is a two-player game between an attacker and a defender (Fearon 1995). The attacker makes a vexatious proposal to the defender. If it is rejected, war breaks out. As war is costly, it is in the interest of the attacker not to make a request greater than the cost of the war, and it is in the interest of the defender to comply with the request. Therefore, the model predicts the existence of a bargaining space, in which an agreement between the two states can be settled to avoid the cost of the war. The bargaining space exists under the following assumptions: States must agree on the respective probability of winning or losing the war; they must be risk-averse; and the issue at stake must not be indivisible.
If we consider the situation of 2014, we can see that losing Crimea and Donbass can be interpreted as a negotiated settlement and that the game of Figure 1(a) is the representation of Fearon’s bargaining game. Russia presented Ukraine with a fait accompli, controlling the two regions in practice without any military effort. The conflict did not break out because the Russian request was on a divisible issue: a part of Ukraine. For Ukraine, the cost of this loss was less than the cost of the war, and therefore, we find an equilibrium in the Russian annexation, as predicted by the bargaining model.
The three-player game makes the role of alliances explicit. In 2014, the game in Figure 1(a) was identified, after the one in Figure 1(b) had been ruled out. As the struggle was limited to a territorial dispute that was not considered relevant for the US/NATO, Not support was its dominating strategy. This is a worthwhile conclusion, as the NATO expansion has often been considered the main cause of conflict (Mearsheimer 2014); our explanation proves that this cause is inconsistent with the course of events: the US/NATO did not interfere in the Crimea’s annexation.
Conversely, the situation of 2022 led to the outbreak of war. Let’s see how our explanation complements the conclusions of the bargaining model. From the tenets of that model, wars can be explained by the actions of three mechanisms:
Private Information and incentives to misrepresent.
Commitment problems.
Issue indivisibility.
Regarding point 1, the role of this mechanism in the war of 2022 has been discussed in Idrisoglu and Spaniel (2024). Broadly speaking, states have private information about their military capabilities and resolve that cannot be credibly shared with the enemy. In 2022, the Ukrainian resolve was clearly unexpected.
Regarding point 2, the role of this mechanism in the war of 2022 has been discussed in Smith (2024). If bargaining is seen as a dynamic process between two nations whose relative military capabilities change over time, then the declining state can attack an emerging power with a preventive war. Its purpose is to avoid less favourable future agreements. In 2022, Russia may have feared that the victory of the political parties in favour of Western integration might lead to a future development of Ukrainian military capabilities (via NATO membership).
Our three-player model highlights the role of both point 3, that is, the role of issue indivisibility, and point 1 concerning the US/NATO-Russia interaction (the role of a defensive alliance). Comparing 2014 and 2022 and analysing the Russian tactics of the early days of war in 2022, it can be seen that the Russian aim was the conquest of the entire Ukraine, and not a part of it, and therefore the issue at stake was indivisible. The Russian invasion pointed directly at the capital Kyiv, with the obvious aim of replacing the incumbent government with a pro-Russian one. This changed the situation of 2014, summarised in Figure 1, into the one summarised in Figure 2. For Ukraine, to resist Russia was a matter of existence, and therefore it was its dominant strategy. At the same time, the U.S./NATO could not accept the logic of a war of conquest, as it would have entailed a reputational cost unbearable in the long run, thus ending up trapped in the Sanction game.[29]
In the next section, we elaborate on the crucial role of asymmetric/private information in the US/NATO-Russia relations.
3.3 Interpreting Mixed Strategies Through Players’ Utility Functions
There was an inherent randomness in the outbreak of the war in Ukraine, which the alliance dilemma makes explicit through the equilibrium conditions in mixed strategies. The role of randomness in war has been recognised in Gartzke (1999), in which Von Clausewitz’s assertion, “In the whole range of human activities, war most closely resembles a game of cards”, is fully discussed in its application to the bargaining model. In Gartzke, randomness is mainly invoked to describe which type of players are involved in the dispute, whether they are resolute or accommodating.
Before discussing formulas 4(a) and 4(b) as probabilities, it is worth noting that a different interpretation is available. Instead of probabilities, they can be considered as the level of effort in war (for Russia) and in military support (for the US/NATO), with a range between 0 = no effort and 1 = full effort (see Scenario 1 in Tsebelis 1990). This interpretation has some empirical justification, as it is evident that Western support for Ukraine has never reached its maximum capability, with a continuing debate about the level of weapons sophistication more appropriate to defend Kyiv. The same can be said for Russia: it does not seem that it used all its capabilities in the war. Moreover, as it happens for all 2 × 2 games in normal form, the equilibrium condition can be interpreted as the result of a dynamic process in which the two players update their behaviour in reaction to the opponent (see Scenario 4 in Tsebelis 1990).
In the following, we will discuss the consistency of Formulas 4(a) and 4(b) with the existence of private information available to players. In the bargaining model, applied to the Ukrainian war (Idrisoglu and Spaniel 2024), this information is the probability assessment of who will win the war. However, our three-player model resulted in a Sanction game, see Figure 4, between the Invader (Russia) and the Defender (NATO). Therefore, we should discuss the origin of players’ probability assessment that led to the outbreak of war in the framework of the Sanction game. As we will see, the war broke out due to the mutual misunderstanding of probability and utility.
Our interpretation of formulas 4(a) and 4(b) relies on seeing them as an approximation of a game with incomplete information, as suggested by John Harsanyi (1973). The games of Figures 3 and 4 are deduced on the condition that both nations have complete information about their reciprocal gains and costs. However, in the short term, this information is only approximate. A player is aware of their advantages/disadvantages, but the opponent’s cost and payoff can only be guessed, and in our opinion, this is what determined the course of events in 2022. To demonstrate this, we have developed the US/NATO-Russia game shown in Figure 4, including uncertainties about the opponent’s gains and losses. We analyse how these uncertainties affect the equilibrium and decrease or increase the probability of war. This modified game, which will hereon be referred to as the “Invasion Game”, is shown in Figure 5.
The invasion game.
To simplify the notation and highlight the role of uncertainty, all the a ij and b ij parameters are replaced with numbers respecting the outcome rankings. The values that correspond to a 11 = 0 and b 12 = 0 are replaced by two random variables −t r and −t c.[30] They are written with negative signs because they represent costs. The two random variables are the private information of the respective players. The value of t r is the cost suffered by Russia in the case of a war with Ukraine supported by the US/NATO. This value, known by Russia but only guessed by the US/NATO, is subject to a degree of uncertainty and therefore represented by a random variable. To keep the description as simple as possible, we assume that t r is described by a uniform distribution between 0 and x, e.g., t r ∼ U[0, x], with x being the maximum cost of the war, guessed by the US/NATO. At the same time, the value of t c is the reputational cost suffered by the US/NATO for not defending Ukraine. Its actual value is known by the US/NATO, but can only be guessed by Russia, and it is represented by a random variable described by the uniform distribution between 0 and y, e.g., t c ∼ U[0, y], with y being the maximum cost of not supporting. The variables x and y represent the level of uncertainty of the system. The higher the values, the more uncertain each player is about the opponent’s costs.
The outcome of t c and t r determines both sides’ desire for conflict. Decisions can be described in the following way. We assume that there is a threshold r that makes invasion convenient or not. That is, if t r > r, then the cost of a possible war is so high that Russia is better off retreating. At the same time, there is a threshold c that makes it convenient for the US/NATO to support or not. So, if t c > c, then the reputational cost is so high that the US/NATO is better off supporting. The two decisions are intertwined, as suggested by the following analysis. Given that t c and t r are uniform random variables, the probability of a decision can be written explicitly as:
A Russian decision to retreat is rational if its expected value is higher than the expected value of invading. The expected values are:
Note that, conversely to equations (4a) and (4b), any Russian decision depends on Russian parameters and the probability that the US/NATO will react. Retreating is rational if:
that gives
The second equality follows the fact that we have assumed that Russia will retreat if t r > r, in which, the middle term is the definition of r.
The US/NATO’s decision to acquiesce is rational if the expected value of acquiescence is higher than the expected value of supporting. Expected values are:
Note that the US/NATO’s decision depends on US/NATO parameters and the probability of Russia retreating. To Support is rational if:
that gives:
The second equality follows from the fact that we have assumed the US/NATO will react if t c > c, in which the middle term is the definition of c.
An analysis of equations (6a) and (7a) reveals where the players’ utility functions are hidden in the Nash equilibria of equations (4a) and (4b). We can interpret 6(a) and 7(a) as the game’s short-term decisions, and equations (4a) and (4b) as the long-term dynamic of the whole game. Short-term decisions are those made in the last few months before the invasion by discounting uncertainty about the opponent’s costs in each player’s utility function. Long-term equilibrium, on the other hand, appears if the uncertainty is resolved by observing the opponent’s behaviour.
A striking consequence of our distinction between the short and long-term behaviour of the game regards the static analysis of the a ij and b ij parameters in the game’s outcomes. For example, consider the Russian gain a 12 from a war against a defenceless Ukraine, which is indicated as a 12 = 3. If a 12 increases, from equation (5a), the short-term effect is to increase the probability of a Russian invasion, but, observing equations (4a) and (4b), long-term Russian behaviour is not affected by a 12. The long-term effect of a 12 is to increase the US/NATO probability of supporting Ukraine.
However, whether we analyse the short or long term, the decisive role played by chance in the Ukrainian conflict is evident. Russia invaded Ukraine, hoping to win the war quickly, and in any case, considering it unlikely that the West would intervene in Kyiv’s defence. Conversely, the US/NATO considered it unlikely that the territorial dispute would escalate into open war, after estimating that the overall cost to the Kremlin was too high. Each player’s decision was characterised by probabilities, randomness, estimation of mutual utility. They took their risks, and the outcome of the gamble was war.
The final step in our analysis is to ascertain the effect of randomness on the probability of war. Our interest lies in the tactics a player should adopt to avoid a war in the short term. As in the long-term version, the game is characterised by complete information (see Figure 3), and the mixed-strategy Nash equilibrium predicts that the probability of a war is always incumbent and depends only on known payoffs. However, when the game is played in the short term, players can strategically manipulate uncertainty for their own purposes. In other words, they can try to control the x and y parameters by defining the uniform distribution range, and this may affect the probability of a war, at least in the short term.
The equations (6b) and (7b) show how dependency on each other’s decisions passes through the c and r thresholds. Using the 6(b) and 7(b) equations we can determine the values of these thresholds as follows:
and
It is worth noting that when x = 0 and y = 0, system uncertainty disappears and the mixed strategies equilibrium of equations (4a) and (4b) emerges, in line with Harsanyi’s findings (1973). However, when x > 0 and y > 0, strategies are affected by uncertainties. Note that x is the uncertain cost of war for Russia, as perceived by the US/NATO, while y is the uncertain reputational cost to the US/NATO of Not Support, as perceived by Russia. Then, combining 5(a) with 8(b), shows how the probability of Invasion is affected by both x and y:
The derivative of r(x, y)/x concerning x and y is negative, suggesting that uncertainty regarding the opponent’s payoff is a form of deterrence to invasion. In Figure 6(a) we report the function trend as x increases, while fixing y at a specific level, y = 0.1 in this example. In Figure 6(b) we report the function trend as y increases while fixing x at a specific level, x = 0.1 in this example. The two graphs both plot a decrease. However, x and y have different impacts on the probability of invasion. Comparing Figure 6(a) and (b), and more specifically observing the probability range affected by uncertainty, it can be seen that an increase in x decreases the probability of invasion only slightly, from 0.5 to 0.48, while an increase in y decreases the probability of invasion from 0.5 to 0.15. A more accurate numerical comparison should confirm this finding but, in any case, the result suggests that if the US/NATO had maintained a higher level of uncertainty regarding the reputational cost it would incur by not supporting Ukraine, then Russia would have had to face a higher probability of incurring a large-scale war.
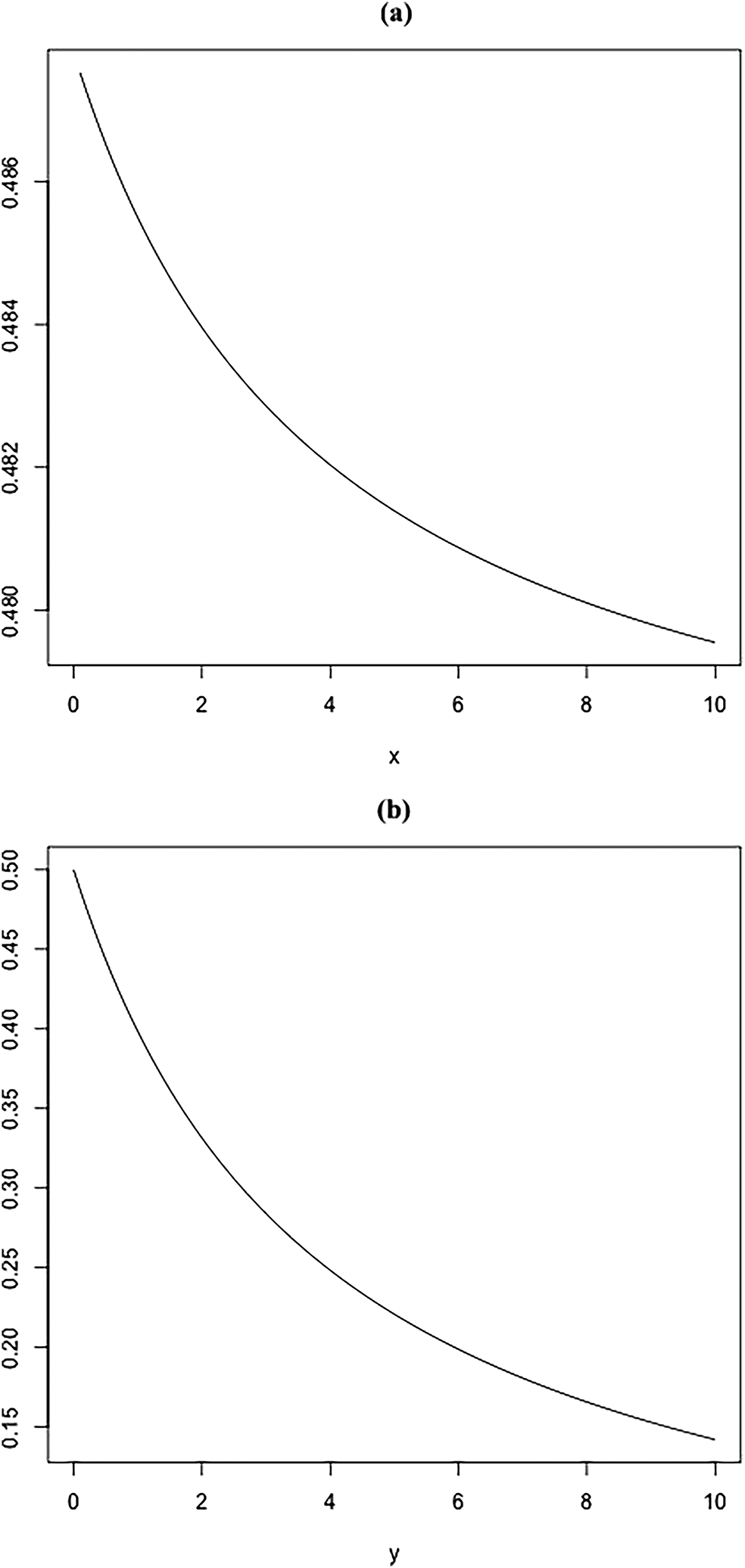
Uncertainty and escalation. (a) Effect of uncertainty x on the probability of invasion. (b) Effect of uncertainty y on the probability of invasion.
Then, combining 5(c) with 8(a), we can measure how a Not Support decision is affected by x and y:
The derivative of c(x, y)/y has a positive relation to x, indicating that the higher the uncertainty of the cost of war to Russia is, the more likely the US/NATO is not to support. So, the derivative of c(x, y)/y has a negative relation to y, suggesting that the more Russia is uncertain about the US/NATO’s reputational cost, the more the US/NATO will tend to support. However, it seems that the uncertainty x has a stronger impact than the uncertainty y. Figure 7(a) shows the probability as x increases, while y is fixed at a specific level, y = 0.1 in this example. And Figure 7(b) shows the probability as y increases, while x is fixed at a specific level, x = 0.1 in this example. The graph in Figure 7(a) has a wider margin of variation than the graph in Figure 7(b). This means that the higher the uncertainty is of Russian costs, the more the US/NATO will tend not to support. This is consistent with general Western expectations, which considered an invasion unlikely because it was deemed too costly for the Russian economy. Conversely, the uncertainty y of the US/NATO’s reputational cost seems to have little effect on the probability of not supporting.
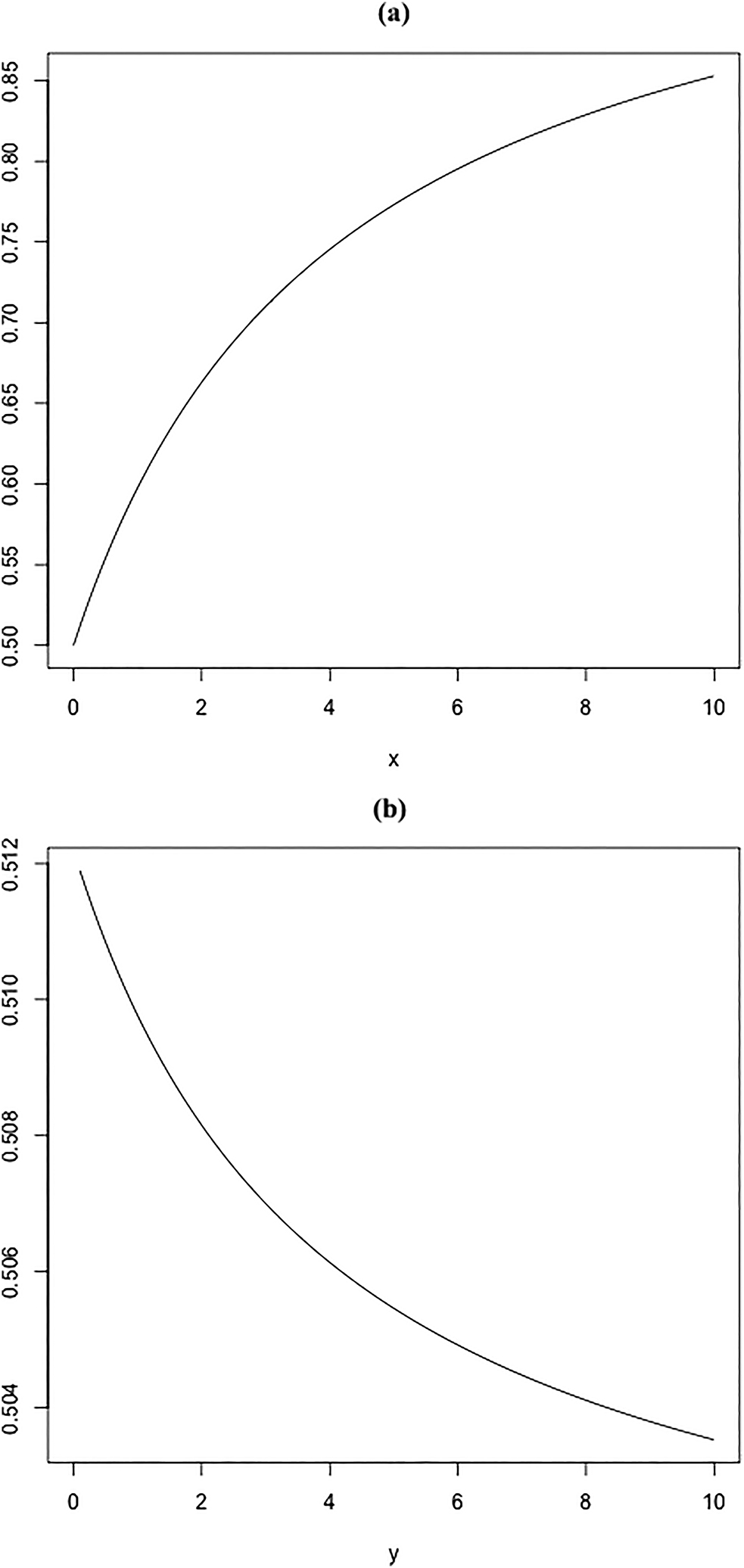
Uncertainty and concession. (a) Effect of uncertainty x on the probability of conceding. (b) Effect of uncertainty y on the probability of conceding.
4 Conclusions
A game theory-based analysis of a current military crisis has twofold value: first, it can provide a theoretical-informed study of a relevant international event, allowing political scientists to contribute to the political debate, including with policy recommendations; second, and most importantly, it demonstrates that it is possible to produce scientifically rigorous analyses even when archival data are not yet available and it is not possible to resort to more in-depth research methods, such as process tracing (Wolford 2024).
The main scientific result of this analysis is that the outcome of the Ukraine-Russia crisis in the early days of 2022 was unpredictable. Due to the non-existence of pure-strategies equilibria, decisions were taken randomly. The model points to main players approaching the breaking point of February 24th, 2022, without a dominant strategy that would have allowed them to act consistently with their preference matrix under conditions of information asymmetry. Both players opted to “stand firm” as the result of a decision-making hazard. In other words, the war onset resulted from the increased non-predictability of the other’s preference matrix.
Separating the long-term from the short-term dynamic of the game, we investigate how players can affect the probability of certain outcomes, our focus being on which tactics can decrease the probability of a war. This analysis involves embedding players’ decisions in a normal-form game, in which decisions are made without knowing how opponents are behaving. This makes the calculation of equilibria tractable with no great mathematical complexities. But it also involves considerable simplification, as the model loses any dynamic representation of events. In fact, other authors have developed similar models as extensive-form games (Zagare 2019), and an interesting direction for future research would be to develop our model in the same way.
References
Benson, B., A. Meirowitz, and K. W. Ramsay. 2014. “Inducing Deterrence through Moral Hazard in Alliance Contracts.” Journal of Conflict Resolution 58 (2): 307–35. https://doi.org/10.1177/0022002712467936.Search in Google Scholar
CRS (Congressional Research Service). 2022. Renewed Great Power Competition: Implications for Defense – Issues for Congress. Washington D.C.Search in Google Scholar
de Vogel, S., and J. S. Sun. 2024. “Crisis Bargaining, Domestic Politics and Russia’s Invasion of Ukraine.” Conflict Management and Peace Science 41 (5): 534–55. https://doi.org/10.1177/07388942241237704.Search in Google Scholar
Diesing, P., and G. Snyder. 1977. Conflict among Nations: Bargaining, Decision Making, and System Structure in International Crises. Princeton: Princeton University Press.Search in Google Scholar
Donaldson, R. H., J. L. Nogee, and V. Nadkarni. 2014. “The Foreign Policy of Russia: Changing Systems, Enduring Interests.”. Armonk: M.E. Sharpe.10.4324/9781315699769Search in Google Scholar
Fang, S., J. C. Johnson, and B. A. Leeds. 2014. “To Concede or to Resist? The Restraining Effect of Military Alliances.” International Organization 68 (4): 775–809. https://doi.org/10.1017/s0020818314000137.Search in Google Scholar
Fearon, J. D. 1995. “Rationalist Explanations for War.” International Organization 49 (3): 379–414. https://doi.org/10.1017/s0020818300033324.Search in Google Scholar
Fey, M., and K. W. Ramsey. 2007. “Mutual Optimism and War.” American Journal of Political Science 51 (4): 738–54. https://doi.org/10.1111/j.1540-5907.2007.00278.x.Search in Google Scholar
Freire, M. R., and R. E. Kanet. 2012. Russia and its Near Neighbours. Basingstoke: Palgrave Macmillan.10.1057/9780230390164Search in Google Scholar
Gartzke, E. 1999. “War is in the Error Term.” International Organization 53 (3): 567–87. https://doi.org/10.1162/002081899550995.Search in Google Scholar
Götz, E. 2016a. “Putin, the State, and War: The Causes of Russia’s Near Abroad Assertion Revisited.” International Studies Review 19 (2): 228–53. https://doi.org/10.1093/isr/viw009.Search in Google Scholar
Götz, E. 2016b. “Neorealism and Russia’s Ukraine Policy, 1991–Present.” Contemporary Politics 22 (3): 301–23. https://doi.org/10.1080/13569775.2016.1201312.Search in Google Scholar
Gross, S., and C. Stelzenmüller. 2024. Europe’s Messy Russian Gas Divorce. Brookings Institution. https://www.brookings.edu/articles/europes-messy-russian-gas-divorce/ (accessed January 20, 2025).Search in Google Scholar
Harsanyi, J. 1973. “Games with Randomly Distributed Payoffs: A New Rationale for Mixed Strategy Equilibrium Points.” International Journal of Game Theory 2 (1): 1–23. https://doi.org/10.1007/bf01737554.Search in Google Scholar
Hensel, P. R., S. McLaughlin Mitchell, T. E. Sowers, and C. L. Thyne. 2008. “Bones of Contention: Comparing Territorial, Maritime, and River Issues.” Journal of Conflict Resolution 52 (1): 117–43. https://doi.org/10.1177/0022002707310425.Search in Google Scholar
Idrisoglu, I., and W. Spaniel. 2024. “Information Problems and Russia’s Invasion of Ukraine.” Conflict Management and Peace Science 41 (5): 514–33. https://doi.org/10.1177/07388942241238583.Search in Google Scholar
ISW (Institute for the Study of War). 2019. How We Got Here with Russia: The Kremlin’s Worldview. Institute for the Study of War and the Critical Threats Project at the American Enterprise Institute.Search in Google Scholar
Leeds, B. A. 2003. “The Influence of Military Alliances on the Initiation of Militarized Interstate Disputes.” American Journal of Political Science 47 (3): 427–39. https://doi.org/10.1111/1540-5907.00031.Search in Google Scholar
Leeds, B. A. 2005. “Alliance and the Expansion and Escalation of Militarized Interstate Dispute”, In New Directions for International Relations, edited by A. Mintz and B. Russett. Lanham: MD: Lexington Books.Search in Google Scholar
Lutsevych, O., and J. Wallace. 2022. Ukraine-Russia Relations. Chatham House. https://www.chathamhouse.org/2021/11/ukraine-russia-relations (accessed January 20, 2025).Search in Google Scholar
McLaughlin Mitchell, S. and Vasquez, J. 2024. “The Russia-Ukraine War: What Can Quantitative Conflict Research Tell Us?” In What Do We Know about War?, edited by S. McLaughlin Mitchell and J. Vasquez. Lanham: Rowman and Littlefield.10.5040/9798216427643Search in Google Scholar
Mearsheimer, J. J. 1983. Conventional Deterrence. Ithaca: Cornell University Press.Search in Google Scholar
Mearsheimer, J. J. 2014. “Why the Ukraine Crisis is the West’s Fault”, Foreign Affairs September/October 93 (5): 1–12Search in Google Scholar
Mearsheimer, J. J. 2001. The Tragedy of Great Power Politics. New York: Norton.Search in Google Scholar
Powell, R. 2002. “Bargaining Theory and International Conflict.” Annual Review of Political Science 5 (1): 1–30. https://doi.org/10.1146/annurev.polisci.5.092601.141138.Search in Google Scholar
Rosa, P., and A. Cuppuleri. 2021. “Dangerous Dyads in the Post-Soviet Space: Explaining Moscow’s Military Escalation Decision, 1991-2010.” Italian Political Science Review 51 (3): 355–72. https://doi.org/10.1017/ipo.2020.37.Search in Google Scholar
Schelling, T. 1960. The Strategy of Conflict. New York: Oxford University Press.Search in Google Scholar
Slantchev, B. 2003. “The Principle of Convergence in Wartime Negotiation.” American Political Science Review 78 (382): 621–32.10.1017/S0003055403000911Search in Google Scholar
Smith, B. C. 2024. “Commitment Problems and Russia’s Invasion of Ukraine.” Conflict Management and Peace Science 41 (5): 494–513. https://doi.org/10.1177/07388942241248027.Search in Google Scholar
Snyder, G. H. 1984. “The Security Dilemma in Alliance Politics.” World Politics 36 (4): 461–95. https://doi.org/10.2307/2010183.Search in Google Scholar
Snyder, G. H. 1997. Alliance Politics. Ithaca: Cornell University Press.Search in Google Scholar
Trenin, D. 2009. “Russia’s Spheres of Interest, Not Influence.” The Washington Quarterly 32 (4): 3–22. https://doi.org/10.1080/01636600903231089.Search in Google Scholar
Tsebelis, G. 1990. “Are Sanctions Effective? A Game-Theoretic Analysis.” Journal of Conflict Resolution 34 (1): 3–28. https://doi.org/10.1177/0022002790034001001.Search in Google Scholar
Tsebelis, G. 1993. “Penalty and Crime: Further Theoretical Considerations and Empirical Evidence.” Journal of Theoretical Politics 5 (3): 349–74. https://doi.org/10.1177/0951692893005003003.Search in Google Scholar
Tsygankov, A. 2013. Russia’s Foreign Policy: Change and Continuity in National Identity. Lanham, Ma.: Rowman & Littlefield.Search in Google Scholar
Tsygankov, A. 2015. “Vladimir Putin’s Last Stand: The Sources of Russia’s Ukraine Policy.” Post-Soviet Affairs 31 (4): 279–303. https://doi.org/10.1080/1060586x.2015.1005903.Search in Google Scholar
Tsygankov, A. 2018. “The Sources of Russia’s Fear of NATO.” Communist and Post-Communist Studies 51 (2): 101–11. https://doi.org/10.1016/j.postcomstud.2018.04.002.Search in Google Scholar
Wolford, S. 2024. “The Bargaining Framework and Russia’s Invasion of Ukraine.” Conflict Management and Peace Science 41 (5): 485–93. https://doi.org/10.1177/07388942241244655.Search in Google Scholar
Zagare, F. 2019. Game Theory, Diplomatic History and Security Studies. Oxford and New York: Oxford University Press.10.1093/oso/9780198831587.001.0001Search in Google Scholar
© 2025 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.

