Organizational learning and optimal fiscal and monetary policy

Bidyut Talukdar

doi:10.1515/bejm-2012-0002

Artikel

Organizational learning and optimal fiscal and monetary policy

Bidyut Talukdar

Veröffentlicht/Copyright: 21. Mai 2014

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen Erkunden Sie dieses Fachgebiet

Aus der Zeitschrift The B.E. Journal of Macroeconomics Band 14 Heft 1

Abstract

We study optimal fiscal and monetary policy in a Ramsey economy where firms learn from their production experience and incur a real cost in changing their prices. Two central results emerge from our study. First, optimal tax policy is counter-cyclical – tax rates fall during recession and rise during boom. This finding contrasts with pro-cyclical tax results obtained in standard sticky price Ramsey models. In presence of learning-by-doing (LBD) mechanism, the Ramsey planner finds it relatively more costly to raise taxes in response to a negative technology shock. Higher taxes would reduce hours, output, and hence future level of organizational capital which will magnify the shock further by lowering future productivity. Hence, in response to a negative productivity shock, the planner finds it optimal to lower taxes in order to raise the after tax return to work and minimize the welfare-reducing effects of the shock. Second, optimal inflation is very stable and persistent over the business cycle. We show that while a dynamic link between current production and future productivity generates the inflation persistence, the real cost of price adjustment is the key factor behind the very low volatility in optimal inflation. Both of these mechanisms work through the monopolistic firms’ optimal pricing condition – namely the New Keynesian Philips Curve.

Keywords: learning-by-doing; optimal fiscal and monetary policy; Ramsey model; sticky prices

JEL Classification: E52; E61; E63

Corresponding author: Bidyut Talukdar, Department of Economics, Saint Mary’s University, 923 Robie Street, Halifax, NS, BCH 3C3 Canada, Tel.: +1 902 496 8164, Fax: +1 902 420 5129, e-mail: bidyut.talukdar@smu.ca

Acknowledgments

I am extremely grateful to Alok Johri for his advice, guidance and encouragement. I would like to thank the associate editor and two anonymous referees for constructive comments, Marc-André Letendre, and William Scarth for helpful discussions and advice, Katherine Cuff, Maxim Ivanov, Stephen Jones, Lonnie Magee, Mike Veall, and seminar participants at Midwest Macro Meetings, Canadian Economics Association Meetings, several universities including McMaster University, and Saint Mary’s University for insightful comments.

Appendix A: The New Keynesian Phillips Curve (NKPC)

We derive the New Keynesian Phillips Curve from intermediate goods producing firms’ profit maximization problem. The representative firm i chooses the plans for n_it, h_it+1, and P_it so as to maximize the present expected discounted value of life-time profits. That is the firms problem is to

(A.1)

maxnit,hit+1,PitE0∑t=0∞QtPt{PitPtyit−wtnit−φ2(PitPit−1−π)2} (A.1)

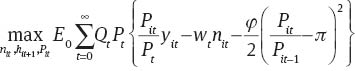
subject to technological constraint on output production

(A.2)

yit=ztnitαhitθ (A.2)

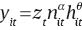
technological constraint on organizational capital accumulation

(A.3)

hi,t+1=(1−δh)hit+hitγyitε, (A.3)

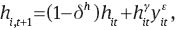
and taking as given the demand function for variety i,

(A.4)

yit≥(PitPt)−ηyt. (A.4)

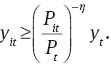
Letting Q_tP_tmc_it, and Q_tP_tΨ_it denote Lagrange multipliers associated with constraints (33) and (34) respectively, the Lagrangian associated with the firm’s optimization problem is

∑t=0∞QtPt{PitPt(PitPt)−ηyt−wtnit−φ2(PitPit−1−π)2+mcit[ztnitαhitθ−(PitPt)−ηyt]+Ψit[(1−δh)hit+hitγ((PitPt)−ηyt)ε−hit+1]}

The first order condition with respect to intermediate firm’s price, P_it, (i.e., the New Keynesian Phillips Curve) is,

(A.5)

(1−η)(PitPt)−ηyt+mcitη(PitPt)−ηyt(PtPit)=ηεΨithitγyitε(PtPit)+φ(PitPit−1−π)(PtPit−1)−Qt+1φ(PitPit−1−π)(Pit+1Pit)(Pt+1Pit). (A.5)

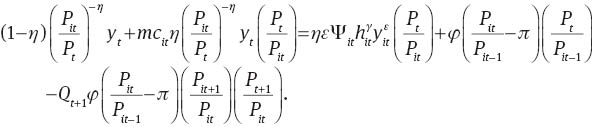
Since all intermediate firms face the same wage rate, face the same downward sloping demand curves, and have access to the same production technology, marginal costs, mc_it, are identical across all firms. Consequently, they hire the same amount of labor and produce the same amount of output. Therefore, we can restrict our attention to a symmetric equilibrium in which all firms make the same decisions. We thus drop all the subscripts i. That is, in equilibrium y_it=y_t, p_it=p_t, mc_it=mc_t, Ψ_it=Ψ_t, n_it=n_t, h_it=h_t. Therefore, equations (36), can be simplified as:

(A.6)

[1−η+ηmct]yt=Ψtηεhtγytε+φ(πt−π)πt−φEt[qt+1(πt+1−π)πt+1], (A.6)

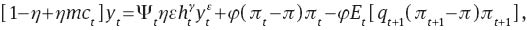
where, πt=PtPt−1, and q_t (=Q_t+1π_t+1) is the real discount factor. After some algebraic manipulations and the substitution of Ψ_t (using equation (21) we have the final form of NKPC as

(A.7)

[η−1η−mct]ηyt=−φ(πt−π)πt+φEt[Qt+1(πt+1−π)πt+1]−Qt+1πt+1[mct+1θyt+1ht+1+Ψt+1{(1−δh)+γht+1γ−1yt+1ε}]ηεhtγytε. (A.7)

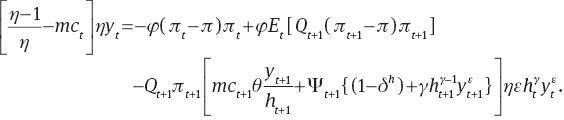
Steady state NKPC

Note that all the (π_t/t₊₁–π) terms become zero in the steady state. Now, imposing steady sate in equation (A.6), and after some algebraic manipulations, we can express the steady-state NKPC as

(A.8)

mc=η−1η+Ψεhγyε−1. (A.8)

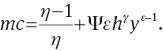
Appendix B: Sensitivity analysis

Table B.5

Sensitivity of dynamic results with respect to the intertemporal elasticity of substitution (CRRA).

Variable	Mean	Std. Dev.	Auto. corr.	Corr(x,y)	Corr(x,g)	Corr(x,z)
φ=1.15
τⁿ	0.2374	0.3856	0.9577	0.7121	0.6118	0.4642
π–1	–2.3978	0.0093	0.9599	–0.1381	0.7042	–0.3437
R–1	1.5040	0.3158	0.8515	–0.2497	–0.6693	0.1562
y	0.7529	0.0054	0.9144	1.0000	0.5308	0.8928
n	0.3310	0.0026	0.9033	–0.2264	0.7508	–0.5688
c	0.6970	0.0052	0.9250	0.8102	–0.2221	0.9603
m/g	0.4335	0.0174	0.9095	–0.3585	0.2708	–0.7820
φ=1.25
τⁿ	0.2375	0.4274	0.9652	0.7404	0.4541	0.4947
π–1	–2.3165	0.0106	0.9600	–0.1785	0.6727	–0.4010
R–1	1.5191	0.3406	0.8097	–0.2602	–0.5986	0.1764
y	0.7139	0.0052	0.9140	1.0000	0.5660	0.9136
n	0.3330	0.0029	0.8816	–0.2365	0.7155	–0.6123
c	0.6760	0.0049	0.9270	0.7926	–0.2124	0.9597
m/g	0.4337	0.0170	0.8831	–0.4572	0.2302	–0.7948

Table B.6

Sensitivity of dynamic results with respect the elasticity of substitution between monopolistically competitive goods.

Variable	Mean	Std. Dev.	Auto. corr.	Corr(x,y)	Corr(x,g)	Corr(x,z)
η=5
τⁿ	0.2416	0.3387	0.9470	0.7275	0.8058	0.4730
π–1	–2.5895	0.0408	0.9146	–0.0029	0.7551	–0.4524
R–1	1.3442	0.2117	0.9179	–0.1979	–0.8212	0.2389
y	0.8305	0.0122	0.9005	1.0000	0.4865	0.8358
n	0.3138	0.0033	0.9106	–0.0437	0.8068	–0.5373
c	0.6887	0.0106	0.8977	0.7578	–0.1364	0.9873
m/g	0.4476	0.0085	0.9270	–0.4650	0.3555	–0.7883
η=7
τⁿ	0.2254	0.3187	0.9577	0.6335	0.8359	0.3687
π–1	–2.4102	0.0412	0.9324	–0.0008	0.7638	–0.4277
R–1	1.5397	0.1725	0.9409	–0.2544	–0.6542	0.0593
y	0.8826	0.0133	0.9009	1.0000	0.4646	0.8504
n	0.3335	0.0033	0.9136	–0.0250	0.8352	–0.4982
c	0.7319	0.0118	0.8975	0.7729	–0.1387	0.9876
m/g	0.4461	0.0080	0.9500	–0.4394	0.3496	–0.7282

Table B.7

Sensitivity of dynamic results with respect to the the degree of substitution between cash and credit goods.

Variable	Mean	Std. Dev.	Auto. corr.	Corr(x,y)	Corr(x,g)	Corr(x,z)
σ=0.60
τⁿ	0.2325	0.3191	0.9519	0.7229	0.6116	0.5293
π–1	–2.3627	0.0481	0.9562	0.1087	0.7360	–0.3930
R–1	1.6502	0.2830	0.9201	–0.2125	–0.1388	0.1298
y	0.8609	0.0131	0.9030	1.0000	0.5487	0.7909
n	0.3252	0.0038	0.9197	0.0722	0.8347	–0.4968
c	0.7138	0.0108	0.8939	0.7714	–0.0470	0.9930
m/g	0.4494	0.0142	0.9706	–0.1359	0.4625	–0.6360
σ=0.64
τⁿ	0.2337	0.3479	0.9256	0.5942	0.8677	0.3477
π–1	–2.5320	0.0354	0.8809	–0.0813	0.7389	–0.4619
R–1	1.4461	0.2824	0.8902	–0.0734	–0.8322	0.3265
y	0.8614	0.0128	0.8999	1.0000	0.4181	0.8765
n	0.3254	0.0030	0.9087	–0.1064	0.8102	–0.5283
c	0.7143	0.0118	0.8999	0.7699	–0.1927	0.9757
m/g	0.4251	0.0066	0.9004	–0.6092	0.2125	–0.7553

Table B.8

Sensitivity of dynamic results with respect the the price stickiness parameter.

Variable	Mean	Std. Dev.	Auto. corr.	Corr(x,y)	Corr(x,g)	Corr(x,z)
ϕ=4
τⁿ	0.2337	0.3262	0.9531	0.6747	0.8279	0.4119
π–1	–2.4865	0.0596	0.9250	–0.0034	0.7608	–0.4392
R–1	1.4563	0.1685	0.9297	–0.2529	–0.7249	0.1037
y	0.8613	0.0128	0.9007	1.0000	0.4732	0.8448
n	0.3254	0.0033	0.9123	–0.0339	0.8235	–0.5149
c	0.7142	0.0113	0.8976	0.7668	–0.1381	0.9875
m/g	0.2468	0.0080	0.9405	–0.4682	0.3404	–0.7663
ϕ=7
τⁿ	0.2319	0.3267	0.9529	0.6726	0.8283	0.4109
π–1	–2.4858	0.0345	0.9248	–0.0052	0.7607	–0.4398
R–1	1.4569	0.1884	0.9342	–0.2243	–0.7658	0.1598
y	0.8613	0.0128	0.9007	1.0000	0.4718	0.8456
n	0.3254	0.0033	0.9122	–0.0354	0.8233	–0.5150
c	0.7142	0.0113	0.8976	0.7669	–0.1394	0.9872
m/g	0.4468	0.0081	0.9404	–0.4614	0.3528	–0.7647

References

Argote, L., S. L., Beckman, and D. Epple. 1990. “The Persistence and Transfer of Learning in Industrial Settings.” Management Science 36: 140–154.10.1287/mnsc.36.2.140Suche in Google Scholar

Atkeson, A., and P. J. Kehoe. 2005. “Modeling and Measuring Organization Capital.” Journal of Political Economy 113: 1026–1053.10.1086/431289Suche in Google Scholar

Bahk, B. H., and M. Gort. 1993. “Decomposing Learning by doing in New Plants.” Journal of Political Economy 101: 561–583.10.1086/261888Suche in Google Scholar

Benkard, C. L. 2000. “Learning and Forgetting: The Dynamics of Aircraft Production.” American Economic Review 90: 1034–1054.10.1257/aer.90.4.1034Suche in Google Scholar

Calvo, G. A., and P. E. Guidotti. 1993. “On the Flexibility of Monetary Policy: The Case of the Optimal Inflation Tax.” Review of Economic Studies 60: 667–687.10.2307/2298130Suche in Google Scholar

Chang, Y., J. F. Gomes, and F. Schorfheide. 2002. “Learning-by-doing as a Propagation Mechanism.” American Economic Review 92: 1498–1520.10.1257/000282802762024601Suche in Google Scholar

Chari, V., and P. J. Kehoe. 1999. “Chapter 26 Optimal Fiscal and Monetary Policy.” In Part 3 of Handbook of Macroeconomics, edited by John B. Taylor and Michael Woodford, vol. 1, 1671–1745. Elsevier.10.1016/S1574-0048(99)10039-9Suche in Google Scholar

Chari, V. V., L. J. Christiano, and P. J. Kehoe. 1991. “Optimal Fiscal and Monetary Policy: Some Recent Results.” Journal of Money, Credit and Banking 23: 519–539.10.2307/1992686Suche in Google Scholar

Chugh, S. K. 2006. “Optimal Fiscal and Monetary Policy with Sticky Wages and Sticky Prices.” Review of Economic Dynamics 9: 683–714.10.1016/j.red.2006.07.001Suche in Google Scholar

Chugh, S. K. 2007. “Optimal Inflation Persistence: Ramsey Taxation with Capital and Habits.” Journal of Monetary Economics 54: 1809–1836.10.1016/j.jmoneco.2006.07.005Suche in Google Scholar

Chugh, S. K. 2009. “Does the Timing of the Cash-in-advance Constraint Matter for Optimal Fiscal and Monetary Policy?” Macroeconomic Dynamics 13: 133–150.10.1017/S1365100509080158Suche in Google Scholar

Cooper, R., and A. Johri. 2002. “Learning-by-doing and Aggregate Fluctuations.” Journal of Monetary Economics 49: 1539–1566.10.1016/S0304-3932(02)00180-0Suche in Google Scholar

Darr, E. D., L. Argote, and D. Epple. 1995. “The Acquisition, Transfer, and Depreciation of Knowledge in Service Organizations: Productivity in Franchises.” Management Science 41: 1750–1762.10.1287/mnsc.41.11.1750Suche in Google Scholar

Ericson, R., and A. Pakes. 1995. “Markov-perfect Industry Dynamics: A Framework for Empirical Work.” Review of Economic Studies 62: 53–82.10.2307/2297841Suche in Google Scholar

Faia, E., and T. Monacelli. 2007. “Optimal Interest Rate Rules, Asset Prices, and Credit Frictions.” Journal of Economic Dynamics and Control 31: 3228–3254.10.1016/j.jedc.2006.11.006Suche in Google Scholar

Gunn, C., and A. Johri. 2011. “News and Knowledge Capital.” Review of Economic Dynamics 14: 92–101.10.1016/j.red.2010.07.003Suche in Google Scholar

Irwin, D. A., and P. J. Klenow. 1994. “Learning-by-doing Spillovers in the Semiconductor Industry.” Journal of Political Economy 102: 1200–1227.10.1086/261968Suche in Google Scholar

Jarmin, R. S. 1994. “Learning by doing and Competition in the Early Rayon Industry.” The RAND Journal of Economics 25: 441–454.10.2307/2555771Suche in Google Scholar

Johri, A. (2009) “Delivering Endogenous Inertia in Prices and Output.” Review of Economic Dynamics 12: 736–754.10.1016/j.red.2009.03.001Suche in Google Scholar

Johri, A., and A. Lahiri. 2008. “Persistent Real Exchange Rates.” Journal of International Economics 76: 223–236.10.1016/j.jinteco.2008.07.003Suche in Google Scholar

Johri, A., and B. Talukdar. 2011. “Organizational Capital and Optimal Ramsey Taxation.” Department of Economics Working Papers 2011-09. McMaster University.Suche in Google Scholar

Lev, B., and S. Radhakrishnan. 2005. “The Valuation of Organization Capital.” In Measuring Capital in the New Economy, edited by Carol Corrado, John Haltiwanger and Dan Sichel, 73–110. National Bureau of Economic Research, Inc. NBER Chapters.10.7208/chicago/9780226116174.003.0004Suche in Google Scholar

Lucas, R. E., and N. L. Stokey. 1983. “Optimal Fiscal and Monetary Policy in an Economy without Capital.” Journal of Monetary Economics 12: 55–93.10.1016/0304-3932(83)90049-1Suche in Google Scholar

Prescott, E. C., and M. Visscher. 1980. “Organization Capital.” The Journal of Political Economy 88: 446–461.10.1086/260879Suche in Google Scholar

Ramsey, F. P. 1927. “A Contribution to the Theory of Taxation.” The Economic Journal 37: 47–61.10.2307/2222721Suche in Google Scholar

Rosen, S. 1972. “Learning by Experience as Joint Production.” The Quarterly Journal of Economics 86, 366–382.Suche in Google Scholar

Rotemberg, J. J. 1982. “Sticky Prices in the United States.” Journal of Political Economy 90: 1187–1211.10.1086/261117Suche in Google Scholar

Schmitt-Grohé, S., and M. Uribe. 2004a. “Optimal Fiscal and Monetary Policy Under Imperfect Competition.” Journal of Macroeconomics 26: 183–209.10.1016/j.jmacro.2003.11.002Suche in Google Scholar

Schmitt-Grohé, S., and M. Uribe. 2004b. “Optimal Fiscal and Monetary Policy Under Sticky Prices.” Journal of Economic Theory 114: 198–230.10.1016/S0022-0531(03)00111-XSuche in Google Scholar

Schmitt-Grohé, S., and M. Uribe. 2004c. “Solving Dynamic General Equilibrium Models Using a Second-order Approximation to the Policy Function.” Journal of Economic Dynamics and Control 28: 755–775.10.1016/S0165-1889(03)00043-5Suche in Google Scholar

Schmitt-Grohé, S., and M. Uribe. 2006. “Optimal Fiscal and Monetary Policy in a Medium-scale Macroeconomic Model.” Working Paper Series 612. European Central Bank.10.2139/ssrn.891011Suche in Google Scholar

Schmitt-Grohé, S., and M. Uribe. 2007. “Optimal Simple and Implementable Monetary and Fiscal Rules.” Journal of Monetary Economics 54: 1702–1725.10.1016/j.jmoneco.2006.07.002Suche in Google Scholar

Siu, H. E. 2004. “Optimal Fiscal and Monetary Policy with Sticky Prices.” Journal of Monetary Economics 51: 575–607.10.1016/j.jmoneco.2003.07.008Suche in Google Scholar

Talukdar, B. 2013. “Learning-by-doing and Optimal Ramsey Interest Rate.” Manuscript, Saint Mary’s University.Suche in Google Scholar

Talukdar, B. 2014. “Learning-by-doing, Intangible Capital and Optimal Markup Variations.” Manuscript, Saint Mary’s University.Suche in Google Scholar

Thornton, R. A., and P. Thompson. 2001. “Learning from Experience and Learning from Others: An Exploration of Learning and Spillovers in Wartime Shipbuilding.” American Economic Review 91: 1350–1368.10.1257/aer.91.5.1350Suche in Google Scholar

Woodford, M. D. 2003. Interest and Prices. Princeton, New Jersey: Princeton University Press.Suche in Google Scholar

Published Online: 2014-5-21

Published in Print: 2014-1-1

Sie haben derzeit keinen Zugang zu diesem Inhalt.

Artikel in diesem Heft

https://doi.org/10.1515/bejm-2012-0002

Schlagwörter für diesen Artikel

learning-by-doing; optimal fiscal and monetary policy; Ramsey model; sticky prices